 |
Оценка структуры временного ряда: наличие тренда, сезонности, цикличности, случайной компоненты – по автокорреляционной функции временного ряда и коррелограмме
|
|
|
|
При наличии тенденции и сезонных колебаний значения каждого последующего уровня ряда зависят от предыдущих значений. Корреляционную зависимость между последовательными уровнями временного ряда определяют автокорреляцией уровней ряда.
Для обеспечения статистической достоверности коэффициентов автокорреляции определите число периодов, по которым рассчитывается коэффициент автокорреляции по правилу: максимальный лаг должен быть не меньше n /4 = 16/4 = 4. На листе «Исходные данные» в ячейку D1 введите название «Период». В ячейки D2:D10 введите значения 1,2,…,9 (число периодов t).
В ячейку E1 введите название «Коэф. автокор.».
В ячейку E2 введите формулу коэффициента корреляции r1
= КОРРЕЛ(B2:B16;B3:B17).
В ячейку E3 введите формулу коэффициента корреляции r2
= КОРРЕЛ(B2:B15;B4:B17).
Остальные коэффициенты автокорреляции рассчитайте по формулам, приведенным на рисунке 18 в столбце Е.

Рисунок 18 – Формулы для расчета коэффициентов автокорреляции
и для проверки их значимости
В ячейку D13 введите MAX.
В ячейку E13 введите формулу = МАКС(E2:E10).
Коэффициенты автокорреляции вычислены по выборкам различного объема, что влияет на проверку гипотезы об их значимости.
В ячейку F1 введите название «Объем выборки».
В ячейки F2:F10 введите соответствующие объемы выборок 15, …, 7 (см. рисунок 18, столбец F).
Для проверки на значимость коэффициентов автокорреляции выполните следующие действия:
· в ячейку G1 введите название «Значимость коэффициентов автокорреляции»;
· в ячейки G2, G3, …, G10 введите t1, t2, …, t10 соответственно;
· в ячейку H2 введите формулу = E2*КОРЕНЬ((15 – 2)/(1 – E2^2));
· в ячейки H3:H10 введите остальные формулы, приведенные на рисунке 18 в столбце Н.
|
|
|
Вычислите критические значения статистики:
· в ячейку I1 введите tкр;
· в ячейки I2:I10 введите формулы, приведенные на рисунке 18
в столбце I.
Для построения коррелограммы выполните следующие действия:
· на панели инструментов активизируйте кнопку Мастер диаграмм (шаг 1 из 4), в одноименном диалоговом окне среди стандартных типов выберите График и во второй строке первый график с маркерами, помечающими точки данных, и нажмите кнопку Далее>;
· открывается диалоговое окно Мастер диаграмм (шаг 2 из 4),
в котором во вкладке Диапазон данных в поле Диапазон введите ссылку на ячейки E2:E10; во вкладке Ряд в поле Подписи оси Х введите ссылку на ячейки D2:D10 значений t, в поле Имя – название «Коэффициенты автокорреляции уровней»; нажмите кнопку Далее>;
· откройте диалоговое окно Мастер диаграмм (шаг 3 из 4), в котором во вкладке Заголовки в поле Заголовок диаграммы введите название «Коррелограмма», в поле Ось Х(категорий) введите название «Периоды», в поле Ось Y (значений) – название «Коэффициенты автокорреляции уровней»; во вкладке Легенда снимите флажок Добавить легенду и нажмите кнопку Далее>;
· в открывшемся диалоговом окне Мастер диаграмм (шаг 4 из 4)
в поле имеющемся установите флажок; нажмите кнопку Готово.
Известно, что если наиболее высоким окажется коэффициент автокорреляции порядка t > 1, то ряд содержит сезонные компоненты
с периодом t, тренд и случайную компоненту; если t = 1, то ряд содержит только тренд и случайную компоненту.
Коэффициент автокорреляции первого порядка равен 0,165 (рисунок 19), он незначим, так как 0,6 < 2,1. Аналогично определяется незначимость коэффициента автокорреляции третьего порядка. Это свидетельствует о слабой зависимости текущих уровней ряда уt от уровней уt-1 и уt-3. Наблюдается заметная зависимость текущих уровней ряда уt от уровней уt-2.
Наибольшим по значению является коэффициент автокорреляции четвертого порядка, он равен 0,98, поэтому ряд содержит сезонную компоненту с периодом 4 квартала. Так как значение коэффициента близко к единице, то можно предположить наличие линейного тренда во временном ряде (рисунок 19).
|
|
|

Рисунок 19 – Коэффициенты автокорреляции и проверка их значимости
Таким образом, анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в 4 квартала, что также видно на коррелограмме (рисунок 20).
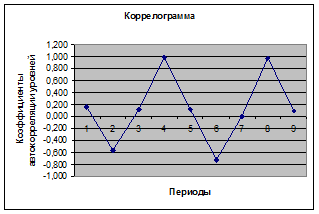
Рисунок 20 – График а втокорреляционной функции
Данный вывод подтверждается и графическим анализом структуры ряда на рисунке 17, так как корреляционное поле имеет «пилообразную» структуру.
|
|
|


