 |
Нормальность распределения остатков
|
|
|
|
Проанализируем нормальность распределения остатков для возможности использования критерия Стьюдента при проверке статистических гипотез. Сделать вывод о нормальности распределения остатков можно следующим образом:
· по гистограмме остатков;
· по числовым характеристикам асимметрии и эксцессу;
· по критерию Пирсона.
 Остатки (отклонения наблюдаемых значений от теоретических) являются оценками случайного члена e уравнения регрессии.
Остатки (отклонения наблюдаемых значений от теоретических) являются оценками случайного члена e уравнения регрессии.
Анализируя качество модели, необходимо проверить ряд статистических гипотез, использующих критерий Стьюдента, которым можно воспользоваться в случае, когда остатки распределены по нормальному закону.
Кривая плотности нормального распределения задается функцией
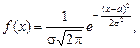
где a – математическое ожидание;
s – среднее квадратическое отклонение.
Например, при а = 0 и s = 1 кривая имеет вид, приведенный на рисунке 3.
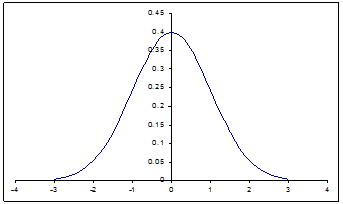
Рисунок 3 – Кривая нормального распределения
Визуально нормальность распределения остатков можно определить, сравнивая кривую плотности нормального распределения с гистограммой частот (частостей) остатков, т. е. со ступенчатой фигурой, состоящей из прямоугольников, основаниями которых служат интервалы одинаковой длины на оси Ох,
а высоты равны сумме частот значений остатков, попадающих в интервал. Если линия, соединяющая середины верхних сторон прямоугольников, близка к кривой плотности нормального распределения, то предполагают, что распределение остатков приближено к нормальному.

 Асимметрия и эксцесс как числовые характеристики нормально распределенной случайной величины равны 0. При асимметричном распределении вершина кривой сдвинута относительно ординаты выборочной средней. Если асимметрия больше 0, то вершина сдвинута вправо (положительная асимметрия), если меньше 0, то – влево (отрицательная асимметрия) (рисунок 4).
Асимметрия и эксцесс как числовые характеристики нормально распределенной случайной величины равны 0. При асимметричном распределении вершина кривой сдвинута относительно ординаты выборочной средней. Если асимметрия больше 0, то вершина сдвинута вправо (положительная асимметрия), если меньше 0, то – влево (отрицательная асимметрия) (рисунок 4).
|
|
|
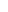
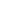

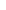








|
|
|
|
|
|
а б
Рисунок 4 – Правосторонняя (а) и левосторонняя (б)
асимметрии распределения
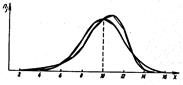
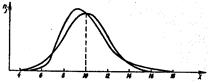
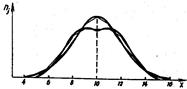
Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение, отрицательный эксцесс – относительно сглаженное распределение (рисунок 5).
 | |||
 | |||



|




|
|
|
|
|

а б
Рисунок 5 – Положительный (а) и отрицательный (б)
эксцессы распределения
Оценки вида кривой Гаусса и значений асимметрии и эксцесса являются качественными характеристиками распределения. Для надежности вывода (с вероятностью 0,95) проверяется статистическая гипотеза о нормальности распределения
с помощью критерия согласия Пирсона. Выдвигается гипотеза о нормальном законе распределения остатков. Для проверки данной гипотезы используется статистика c2 = 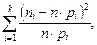 имеющая распределение c2 с (k – r – 1) степенями свободы, где r – число параметров распределения F (x), которые оцениваются по выборке, n – объем выборки; k – число непересекающихся интервалов выборочных значений, ni – число значений выборки, принадлежащих i -му интервалу, i = 0,1,¼, k – 1; pi – вероятности попадания значений случайной величины в каждый из этих интервалов. По выборке вычисляется наблюдаемое значение статистики
имеющая распределение c2 с (k – r – 1) степенями свободы, где r – число параметров распределения F (x), которые оцениваются по выборке, n – объем выборки; k – число непересекающихся интервалов выборочных значений, ni – число значений выборки, принадлежащих i -му интервалу, i = 0,1,¼, k – 1; pi – вероятности попадания значений случайной величины в каждый из этих интервалов. По выборке вычисляется наблюдаемое значение статистики 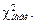 Для выбранного уровня значимости a по распределению c2 находится число
Для выбранного уровня значимости a по распределению c2 находится число  = c2(a; k – r – 1). Гипотеза о нормальном распределении случайного члена принимается на заданном уровне значимости, если
= c2(a; k – r – 1). Гипотеза о нормальном распределении случайного члена принимается на заданном уровне значимости, если 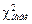 <
<  Если же
Если же 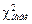 ³
³  то гипотеза отвергается.
то гипотеза отвергается.
|
|
|

· Построим гистограмму остатков. Соединим середины верхних сторон прямоугольников гистограммы и получим полигон распределения, по которому визуально можно предположить закон распределения (рисунок 6).

|


|

Рисунок 6 – Гистограмма
Поскольку ломаная линия на рисунке 6 близка к кривой нормального распределения, заданной уравнением 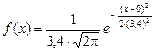 (сравните с рисунком 3), то остатки распределены по нормальному закону. Следовательно, по визуальному анализу гистограммы можно предположить нормальность распределения остатков.
(сравните с рисунком 3), то остатки распределены по нормальному закону. Следовательно, по визуальному анализу гистограммы можно предположить нормальность распределения остатков.
· Асимметричность равна –0,36 (левосторонняя асимметричность эмпирической кривой относительно теоретической), эксцесс равен 0,1 («островершинность» эмпирической кривой), т. е. характеристики плотности распределения (асимметричность и эксцесс) незначительно отличаются от нуля, поэтому можно считать распределение нормальным.
· Подтвердим нормальность распределения с помощью критерия Пирсона.
На листе «Регрессия»найдены наблюдаемое и критическое значения статистики хи-квадрат (таблица 8).
Таблица 8 – Проверка критерия Пирсона
| хи-кв набл | 3,16 |
| хи-кв кр | 7,81 |
Наблюдаемое значение, равное 3,16, меньше хи-квадрат критического, равного 7,81, поэтому остатки распределеныпо нормальному закону.
4.3. Значимость коэффициентов регрессии: проверка значимости коэффициентов регрессии
Проверка значимости коэффициентов регрессии осуществляется с помощью t - статистики Стьюдента. Вычисляются наблюдаемые значения 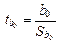 и и 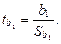 По таблице критических точек распределения Стьюдента по заданному уровню значимости a и числу степеней свободы v = n – 2 находится критическая точка По таблице критических точек распределения Стьюдента по заданному уровню значимости a и числу степеней свободы v = n – 2 находится критическая точка 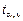 = tкр. Если = tкр. Если 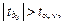 то коэффициент регрессии b 0 значим. Если то коэффициент регрессии b 0 значим. Если 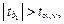 то коэффициент регрессии b 1 значим. Значимость коэффициентов подтверждает правильность выбора модели на этапе спецификации. Если хотя бы один из коэффициентов не значим, то необходимо вернуться на этап спецификации. то коэффициент регрессии b 1 значим. Значимость коэффициентов подтверждает правильность выбора модели на этапе спецификации. Если хотя бы один из коэффициентов не значим, то необходимо вернуться на этап спецификации.
|
Значимость коэффициентов регрессии оценивается с помощью
t -статистики, значения которой получены на листе «Регрессия»
(см. таблицу 5).
Наблюдаемое значение статистики tнабл для коэффициента b 0 равно 115,59 (оно равно отношению точечной оценки коэффициента b 0 к его стандартной ошибке). Критическое значение tкр равно 2,1. Поскольку |tнабл| = 115,59 > tкр = 2,1, то коэффициент b 0 значим.
|
|
|
Аналогично для коэффициента b 1 имеем следующее: tнабл = 5,26, tкр = 2,1. Поскольку |tнабл| = 5,26 > tкр = 2,1, поэтому коэффициент b 1 значим. Для коэффициента b 2 имеем: |tнабл| = 41,85 > tкр = 2,1, поэтому коэффициент b 2 значим.
Значимость коэффициентов регрессии подтверждает выдвинутое на этапе спецификации предположение о линейной форме зависимости факторов.
|
|
|


