Угловая скорость. Угловое ускорение.

Пространство и время. Система отсчета

 

Механическое движение происходит в пространстве и времени. Положение тела в пространстве может быть определено только по отноше­нию к другим телам. Для описания механического движения необходимо указать тело (или систему неподвижных друг относительно друга тел), относительно которого рассматривается движение. Это тело называют телом отсчета.

С телом отсчета связывается система коор­динат. Простейшей системой координат является прямоугольная декартова система x, y, z (рис. 1.1). Координаты тела позволяют установить его положение в пространстве. Движение происхо­дит не только в пространстве, но и во времени; следовательно, для определения моментов вре­мени, которым соответствуют различные поло­жения движущегося тела, необходимо иметь часы отсчитывающие промежутки времени от произвольно выбираемого начального момента.

Тело отсчета, связанные с ним система координат и часы образу­ют систему отсчета. Пространственно-временное описание движе­ния возможно только тогда, когда выбрана определенная система от­счета.

В классической механике пространству и времени приписывают аб­солютный характер, линейные масштабы и промежутки времени остают­ся неизменными при переходе от одной системы отсчета к другой, т. е. не зависят от выбора системы отсчета.

В релятивистской механике линейные масштабы и промежутки вре­мени зависят от выбора системы отсчета и в разных системах отсчета будут разными.

Материальная точка. Абсолютно твердое тело

 

При изучении реальных движений тел часто бывает целесообразно абстрагироваться от их размеров. В этих случаях говорят о движении материальной точки.

Материальная точка — тело, размерами которого в данной задаче можно пренебречь.

Материальной точкой считают, например, Землю при рассмотрении ее движения вокруг Солнца.

Любое тело можно считать совокупностью (системой) материаль­ных точек.

Абсолютно твердое тело — система материальных точек, рас­стояние между которыми не изменяется в процессе движения.

 

Рене Декарт (1596—1650) — французский философ, физик, математик, физиолог.

Физические исследования относятся главным образом к механике, оптике, строению Вселенной. Декарт математически вывел закон пре­ломления света, дал теорию магнетизма. В математике первым ввел понятие переменной величины и функции, заложил основы аналитиче­ской геометрии.

 

Любое движение твердого тела можно представить как результат сложения поступательного и вращательного движений.

Движение тела называют поступательным, если любая прямая, соединяющая две любые его тонки, остается все время параллельной самой себе.

При вращательном движении твердого тела все его тонки описы­вают окружности, центры которых лежат на одной прямой — оси вращения.

 

Скорость и ускорение

 

Траектория. Уравнение движения точки.

 

Положение материальной точки А в декартовой системе координат определяется тремя координатами: х, у, z. Иначе: положение точки может быть задано радиусом-вектором r, проведенным из начала системы коор­динат до точки А (рис. 1.1).

При движении материальной точки А конец радиуса-вектора описы­вает в пространстве некоторую линию, называемую траекторией. При движении точки ее радиус-вектор в общем случае изменяется как по мо­дулю, так и по направлению, т. е. радиус-вектор зависит от времени:

 

r = r (t) (1.1а)

 

Векторному уравнению (1.1а) эквивалентна система скалярных уравнений:

 

x = x(t), y =y(t), z = z(t) (1.1б)

 

Уравнения (1.1а) или соответственно (1.16) называют уравнениями движения материальной точки.

Исключая время из уравнений движения, получим уравнение траек­тории движения материальной точки. По форме траектории механиче­ское движение классифицируется на прямолинейное и криволинейное. Траектория данного механического движения в различных системах от­счета может иметь разную форму.

 

Скорость. Ускорение

 

Рассмотрим движение материальной точки на участке криволиней­ной траектории (рис. 1.2). Отсчет времени начнем с момента, когда точка находилась в положении А. Перемещение точки от А до В за промежуток времени ∆ t изображается вектором ∆r. Длина участка траектории АВ, пройденного материальной точкой за промежуток времени ∆ t, называется длиной пути ∆s и является скалярной функцией времени.

 

На участке траектории АВ вектор средней скорости равен и направлен

вдоль хорды АВ в ту же сторону, что и вектор перемещения ∆r (рис. 1.3). Скорость в точке А (мгновенная скорость).

 

 

При ∆ t →0 хорда АВ в пределе совпадает с касательной, поэтому вектор мгновенной скорости v направлен по касательной к траектории в сторону движения (рис. 1.3). Так как модуль вектора ∆r равен длине ds малого участка траектории (пути ds), то

 

(1.2)

 

т.е. модуль скорости равен первой производной пути по времени.

v Единица скорости —-метр в секунду (м/с).

Скорость движения может изменяться как по модулю, так и по на­правлению. Быстрота изменения скорости характеризуется вектором ус­корения а. Изменение скорости на участке АВ траектории за время ∆ t равно ∆v = v - v, где v — скорость в точке A, v₁ — скорость в точке В.

Среднее ускорение — отношение изменения скорости ∆ν к проме­жутку времени ∆t, в течение которого произошло это изменение:

 

 

Вектор среднего ускорения совпадает по направлению с вектором изменения скорости.

Выражение для ускорения в точке А (мгновенного ускорения) можно получить как предел вектора (а) при ∆ t →0:

 

(1.3)

Ускорение — векторная величина, равная первой производной ско­рости по времени.

v Единица ускорения — метр на секунду в квадрате (м/с²).

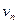Вектор ∆v можно разложить на две составляющие: ∆ — вдоль каса­тельной, ∆ — вдоль нормали. Для этого из точки А по направлению скорости v отложим вектор AD, равный по модулю ∆ . Из рис. 1.4 видно, что ∆ = CD определяет изменение скорости по модулю, вторая состав­ляющая ∆ 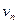характеризует изменение скорости по направлению за промежуток времени ∆ t:

 

 

Полное ускорение а имеет две взаимно перпендикулярные состав­ляющие: — тангенциальное, a_n — нормальное или центростремитель­ное (рис. 1.5).

Тангенциальное ускорение , направленное по касательной, опреде­ляет быстроту изменения модуля скорости.

Модуль тангенциального ускорения равен производной модуля ско­рости по времени:

 

(1.4)

 

Нормальное ускорение характеризует изменение скорости по направле­нию и совпадает с нормалью к траектории к центру ее кривизны. Расчеты показывают, что модуль нормального ускорения

 

(1.5)

 

[ R – радиус кривизны траектории]

 

 

Угловая скорость. Угловое ускорение.

 

При вращательном движении твердого тела его точки, находящиеся на разном расстоянии r от оси вращения, за равные промежутки времени проходят разные пути. Следовательно, они имеют разную скорость и ус­корение (рис. 1.6). Пусть радиус окружности, описываемой некоторой точкой, равен r, а ее линейное перемещение — ds. Тогда угловое пере­мещение (угол поворота радиуса-вектора)

 

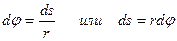(1.6)

 

Кинематическими характеристиками вращательного движения кроме угла поворота являются угловая скорость со и угловое ускорение .

Если за промежуток времени ∆r тело поворачивается на угол , то быстрота его вращения характеризуется угловой скоростью.

Угловая скорость равна первой производной от угла поворота ра­диуса-вектора по времени:

(1.7)

 

Вектор направлен вдоль оси вращения, его направление можно определить, пользуясь правилом правого винта (рис. 1.7).

Если направление вращения винта совпадает с вращением тела, то конец винта укажет направление вектора .

Если = const, то вращательное движение называют равномерным.

Время одного полного поворота тела вокруг оси вращения называ­ют периодом обращения Т, а величину v, обратную периоду, — частотой:

 

 

(1.8)

 

За один период угол поворота радиуса-вектора точки равен 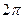рад, поэтому 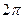= , или

 

 

v Единица угловой скорости — радиан в секунду (рад/с).

Быстрота изменения угловой скорости характеризуется угловым ус­корением. Если за промежуток времени 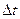угловая скорость получает приращение .

Угловое ускорение равно первой производной от угловой скоро­сти по времени или второй производной от угла поворота радиуса-вектора по времени:

(1.9)

 

Угловое ускорение также является векторной величиной. При уско­ренном вращении совпадает с вектором 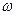, при замедленном вращении противоположно .

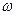v Единица углового ускорения — радиан в секунду в квадрате (рад/с²).

Если угловое перемещение всех точек абсолютно твердого тела оди­наково, то все точки тела имеют одинаковую угловую скорость и одина­ковое угловое ускорение в данный момент времени.

Линейные характеристики — перемещение, скорость, ускорение — различны для разных точек твердого тела. Связь между линейными и угловыми характеристиками движущейся точки можно получить, ис­пользуя равенство (1.6).

Дифференцируя это равенство по времени, получаем

 

(1.10)

 

Дифференцируя равенство (1.6) по времени дважды, получаем соот­ношение между тангенциальным и угловым ускорениями:

 

(1.11)

 

 

12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: