Удар абсолютно упругих и неупругих тел

Рассмотрим процессы столкновения тел. При столкновении проис­ходит их кратковременное взаимодействие, сопровождающееся как де­формацией, так и изменением направления их движения. Примерами яв­ляются упругое и неупругое соударения.

При рассмотрении столкновений необходимо знать форму тел, мас­сы покоя, скорости движения и их упругие свойства. Простейшим видом соударения является центральный удар тел. При этом ударе тела движутся только поступательно, их скорость направлена по прямой, соединяющей центры масс (рис. 1.12). Если удар аб­солютно неупругий, т. е. такой удар, после которого скорость соударяю­щихся тел оказывается одинаковой, то рассматриваемая механическая система является диссипативной[1] и для нее неприменим закон сохранения механической энергии, а применим лишь закон сохранения импульса:

 

p₁+p₂=p

 

Для центрального неупругого удара это соотношение можно переписать в виде

 

(1.40)

 

[v₁ и v₂ — скорость тел, масса которых до взаимодействия m₁ и m₂].

Из формулы (1.40) следует, что после взаимодействия тела будут двигаться как единое целое со скоростью

 

(1.41)

 

Частным случаем рассматриваемого взаимодействия будет такой, когда первоначальные импульсы p₁ и р₂ тел будут равны по модулю, но противоположны по направлению. Тогда результирующая скорость и равна нулю. В этом случае кинетическая энергия взаимодействующих тел полностью переходит во внутреннюю энергию, так как при этом совер­шается работа по деформации тел. В общем случае во внутреннюю энер­гию (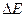) переходит лишь часть кинетических энергий взаимодействую­щих тел:

 

(1.42)

 

Для неупругого удара не выполняется закон сохранения механиче­ской энергии, но справедлив закон сохранения энергии, т. е. полная энер­гия рассматриваемой изолированной системы (сумма всех видов энергии, включая и собственную энергию масс покоя всех частиц) до и после столкновения остается неизменной. При абсолютно упругом столкнове­нии не происходит потеря кинетической энергии, так как в этом случае нет деформации, на которую расходуется часть энергии. Следовательно, для абсолютно упругого удара выполняется закон сохранения механиче­ской энергии и импульса:

 

(1.43)

 

[v₁ и v₂ — скорости соответственно первого и второго тел до удара, а u₁ и u₂ — после удара]. Тогда

 

(1.44)

 

Решая совместно уравнения (1.43) и (1.44), находим скорость перво­го и второго тел после удара:

 

(1.45)

 

Если массы соударяющихся тел равны (m₁=m₂), то, как следует из формул (1.45), u₁= v₂, v₂ = u₁. Тела как бы обмениваются скоростью.

Если масса одного из соударяющихся тел больше другого (m₁>>m₂), а его скорость u₁ = 0, то v₂ = -v₂.

 

Задачи

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

15 ело массой 1 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени задана уравнением s=2t²+4t+1. Определите:

a. работу силы за 10 с с начала ее действия

b. зависимость кинетической энергии от времени

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Дано: m=1кг s=2t²+4t+1

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Найти: а. А b. Е_к=f(t)

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Решение:

 

→→→ Работа, совершаемая силой, выражается через криволинейный интеграл:

 

(1)

 

Сила, действующая на тело, по второму закону Ньютона равна

 

или (2)

 

Мгновенное значение ускорения определяется первой производной от скорости по времени или от второй производной пути по времени. В соответствии с этим находим

 

(3)

 

(4)

 

тогда

 

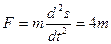(5)

 

из выражения (3) определим

 

(6)

 

подставим (5) и (6) в уравнение (1) и получим

 

 

По этой формуле определим работу, совершаемую силой за 10 с с начала её действия:

 

 

Кинетическая энергия определяется по формуле

 

 

Вычисления:

 

Дж=960 Дж

Ответ: a. A=960 Дж b. T=m(8t²+16t+8)

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

16. На двух шнурах одинаковой длинны, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг (рис.1.13). Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол , и отпустили. На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и не упругим. Определите энергию, израсходованную на деформацию шаров при ударе.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Дано: m₁=0,5 кг m₂=1кг l=0,8 м

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Найти: a. h₁ b.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Решение:

 

→→→ Так как удар шаров неупругий, то после удара шары будут двигаться с общей скоростью v. Закон сохранения количества движения при этом ударе имеет вид

 

(1)

 

[v1 и v2 – это скорость шаров до удара].

 

Скорость большего шара до удара равна нулю (v2=0). Скорость меньшего шара найдем, используя закон сохранения энергии. При отклонении меньшего шара на угол (см. рис.1.13) ему сообщается потенциальная энергия, которая затем переходит в кинетическую:

 

 

Из рисунка видно что

 

поэтому

 

(2)

 

Из уравнений (1)и (2) находим скорость шаров после удара:

 

(3)

 

Кинетическая энергия которой обладают шары послу удара, переходят в потенциальную:

 

(4)

 

[h – это высота падения шаров после столкновения]

Из формулы (4) находим h=v²/(2g), или с учетом (3)

 

 

Вычисления:

 

Ответ: a. h=0,044м b.

 

 

Задачи для самоподготовки

 

17. Тело массой 1 кг под действием постоянной силы движется прямолиней­но. Зависимость пути, пройденного телом, от времени выражается уравнением s = t² + 2t + 2. Определите работу силы за 5 с после начала ее действия.

18. Для того чтобы растянуть пружину на длину х, требуется приложить си­лу F = kх. Какая работа совершается при растяжении пружины на длину x₁? По­тенциальная энергия деформированной пружины . Найдите силу, дейст­вующую на пружину.

19. Тепловоз массой 40 т, двигаясь со скоростью 1 м/с, ударяется в два неподвижных пружинных буфера вагона. Найдите: a. наибольшее сжатие буферов вагона, если коэффициент упругости пружины 5 - 10⁶ Н/м; b. про­должительность удара.

20. На тело действует сила F = kх². На сколько увеличится потенциальная энергия тела при его перемещении из точки х = 0 в точку х - х₁?

21. Стальная цепочка длиной 1 м, лежащая на столе, начинает скользить, ес­ли 0,15 м этой цепочки спущены со стола. Масса цепочки 3 кг, коэффициент тре­ния между столом и цепочкой 0,1. Какая работа против сил трения совершается при соскальзывании всей цепочки?

22. По условию задачи 17 найдите зависимость кинетической энергии от времени и пути.

23. Выведите формулу, по которой вычисляется кинетическая энергия тела массой т, движущегося под действием постоянной силы F, если t = 0, v₀ = 0.

24. Скорость двух центрально соударяющихся шаров до их взаимодействия равна 0,1 и 0,05 м/с, их масса соответственно равна 4 и 3 кг. Определите скорость шаров после удара при упругом соударении.

25. В каком случае двигатель автомобиля совершит большую работу (во сколько раз): для разгона с места до скорости 36 км/ч или при увеличении скоро­сти от 36 до 72 км/ч. Силу сопротивления и время движения в обоих случаях счи­тать одинаковыми.

26. Шар массой 4 кг движется со скоростью 2 м/с и сталкивается с покоя­щимся шаром массой 1 кг. Вычислите работу, совершенную вследствие деформа­ции шаров при прямом центральном ударе. Шары считать неупругими.

 

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: