Формулы поступательного и вращательного движения твердого тела вокруг неподвижной оси

 

Равномерное движение

 

ü Поступательное:

 

(1.12)

ü Вращательное:

 

(1.13)

 

Равнопеременное движение

 

ü Поступательное:

 

(1.14)

 

(1.15)

 

ü Вращательное:

 

(1.16)

 

(1.17)

 

 

ГЛАВА 2 ДИНАМИКА

 

Первый закон Ньютона

 

Динамика

 

Динамика – раздел механики, посвященный изучению движения материальных тел под действием приложенных к ним сил.

В основе классической динамики лежат три закона, сформулирован­ные Ньютоном в труде «Математические начала натуральной филосо­фии» на основании обобщения многочисленных опытных данных.

 

Первый закон Ньютона (закон инерция)

 

Всякое тело сохраняет состояние относительного покоя или рав­номерного прямолинейного движения до тех пор, пока внешнее воз­действие не изменит это состояние.

При отсутствии внешнего воздействия тело, находившееся в движе­нии, продолжает равномерно двигаться по прямой без изменения скорости.

Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными.

К таким системам относится, например, гелиоцентрическая система отсчета, в которой за начало координат принимают Солнце, а оси прово­дят в направлении звезд, которые считаются неподвижными.. Инерциальной будет и другая система (группа систем), которая движется относи­тельно выбранной инерциальной системы равномерно и прямолинейно-поступательно.

Если система отсчета движется по отношению к инерциальной сис­теме с ускорением, то она относится к неинерциальным системам от­счета. В них первый закон Ньютона не выполняется. Система отсчета, связанная с Землей, движется с ускорением, т. е. вращается вокруг Солн­ца и собственной оси. Однако при решении многих задач в земных усло­виях инерциальную систему отсчета связывают с Землей, так как эффек­тами, обусловленными ее неинерциальностью, можно пренебречь.

 

 

Второй закон Ньютона

 

Сила

 

Сила – векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел.

Исаак Ньютон (1643 — 1727) — выдающийся английский ученый, зало­жил основы современного естествознания.

Работы относятся к механике, оптике, астрономии, математике. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал (независимо от Г. Лейбница) дифференциальное и ин­тегральное исчисление. Создал физическую картину мира — ньютоновская теория пространства и времени. Научное творчество Ньютона сыгра­ло исключительно важную роль в истории развития физики.

 

 

Это воздействие проявляется в изменении скорости движущегося те­па или изменении формы и размеров тела.

Сила, как и любая векторная величина, считается заданной, если из­вестны ее числовое значение, направление и точка приложения.

Инертность — свойство тела сохранять состояние покоя или рав­номерного прямолинейного движения. Физическая величина, являющаяся мерой инертности тела при поступательном движении, называется мас­сой. В классической механике () масса тела считается постоянной и равной массе покоя: . Масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит.

При поступательном движении все точки твердого тела за один и тот же промежуток времени совершают равное по величине и направлению перемещение, поэтому скорость и ускорение в данный момент времени всех точек тела одинаковы, следовательно, поступательное движение твердого тела может быть охарактеризовано движением одной точки — центром масс (центром инерции).

Центр масс системы материальных точек — точка, координаты которой определяются следующими соотношениями:

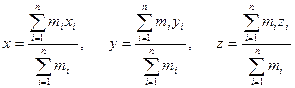(1.18)

 

[ n — число материальных точек; m_i — масса i-й материальной точки сис­темы; х_i, y_i, z_i — координаты i-й материальной точки].

 

 

Второй закон устанавливает связь между динамическими и кинемати­ческими величинами и является основным законом динамики.

Ускорение, приобретаемое материальной точкой (телом) в инер­циальной системе отсчета, пропорционально действующей на точку силе, обратно пропорционально массе материальной точки и по на­правлению совпадает с силой:

(1.19)

 

Если на материальную точку (тело) одновременно действует не­сколько сил, то каждая из этих сил действует независимо от других сил и сообщает точке ускорение, определяемое вторым законом Ньютона.

Ускорение центра масс системы определяется результирующей силой:

 

 

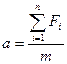
[m – суммарная масса всех точек системы].

Ньютоном второй закон механики был сформулирован не через ус­корение, а через импульс тела (количество движения).

Изменение количества движения (импульса тела) пропорцио­нально приложенной движущей силе и происходит по направлению прямой, по которой эта сила действует.

Импульсом тела называют произведение массы тела на скорость его движения:

(1.20)

 

v Единица импульса — килограмм-метр в секунду (кг * м/с).

Так как , то формулу (1.19) можно записать в виде:

 

(1.21)

 

Формула (1.21) выражает второй закон Ньютона в более общей форме, т.е. когда масса движущегося тела конечных размеров изменяется с течением времени.

v Единицы силы – ньютон (H).

Ньютон – сила, которая телу массой 1 кг сообщает ускорение 1 м/с² в направлении действия силы.

 

Третий закон Ньютона

 

Этот закон утверждает, что силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти тела:

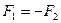(1.22)

Следует отметить, что сила F₁ — это сила, с которой второе тело действует на первое, она приложена к первому телу. F₂ — сила, с которой первое тело действует на второе. Эта сила приложена ко второму телу, поэтому эти силы не уравновешивают друг друга.

При взаимодействии тел наблюдается как прямое действие, так и действие на расстоянии. При прямом действии, например при ударе мо­лота о наковальню, сила, с которой действует молот на наковальню, равна по модулю и противоположна по направлению силе, с которой нако­вальня действует на молот. Примером действия на расстоянии является взаимное притяжение Земли и Солнца. И в этом случае силы равны и противоположно направлены.

 

Закон сохранения импульса

 

Силы взаимодействия между частицами (частями) некоторой рас­сматриваемой системы тел называют внутренними.

Силы, действующие на тела данной системы со стороны тел, не включенных в эту систему, называют внешними.

Если система состоит из n материальных точек, то уравнение (1.21) можно записать в виде

 

[p= -импульс всей системы, - импульс силы].

Перепишем это равенство в виде

 

 

В замкнутой системе силы отсутствуют, т.е. ; следовательно,

 

(1.23)

 

Это равенство выражает закон сохранения импульса: полный вектор импульса замкнутой системы тел с течением времени не изменяется.

Следовательно, если у одного из тел в изолированной системе изме­нился импульс, то это могло произойти только за счет изменения им­пульсов других тел этой же системы.

В неинерциальных системах отсчета закон сохранения импульса не выполняется, так как силы инерции являются внешними некомпенсированными силами по отношению к неинерциальной системе. Однако вто­рой закон Ньютона остается справедливым в данной системе, если в сумму внешних сил включить и силы инерции:

 

 

[ F — сумма внешних сил, F_m — сила инерции].

 

Силы в механике

 

Чтобы предсказать характер движения тела в каждом конкретном случае, необходимо знать законы действующих на тело сил, т. е. зависи­мость сил от различных величин.

ü Силы тяготения (гравитационные силы) — это силы притяжения, которые подчиняются закону всемирного тяготения.

ü Сила тяжести — сипа, с которой тело притягивается Землей.

Под действием силы притяжения к Земле все тела падают в данном месте земного шара с одинаковым ускорением g, называемый ускорением свободного падения. Тогда на основании второго закона Ньютона можно утверждать, что это ускорение вызывается силой тяжести:

 

P = mg. (1.24)

 

ü Вес — сила, с которой тело, притягиваясь к Земле, действует на опору или натягивает нить подвеса.

Сила тяжести равна весу только в том случае, когда ускорение тела относительно Земли равно нулю, т. е. когда тело относительно Земли не­подвижно или движется с постоянной скоростью. В противном случае Р = m(g - а), где а — ускорение тела с опорой относительно Земли.

При свободном падении тела вес этого тела равен нулю, т. е. оно на­ходится в состоянии невесомости.

ü Силы упругости возникают в результате взаимодействия тел, сопро­вождающегося их деформацией.

Упругая (квазиупругая) сила пропорциональна смещению частицы из положения равновесия и направлена к положению равновесия:

 

F = -kr (1.25)

 

[ r — радиус-вектор, характеризующий смещение частицы из положения равновесия, к — упругость].

Примером такой силы является сила упругости деформации пружи­ны при растяжении или сжатии:

 

F=-kx (1.26)

 

[ k —жесткость пружины, х — упругая деформация].

ü Сила трения скольжения возникает при скольжении одного тела

поверхности другого:

 

F_тр=kN (1.27)

 

[ k — коэффициент трения скольжения, зависящий от природы и состоя­ния соприкасающихся поверхностей; N — сила нормального давления, прижимающая трущиеся поверхности друг к другу].

Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению тела относительно другого.

 

Задачи

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

1. Тело брошенное вверх с высоты 12 м под углом 30° к горизонту с начальной скоростью 12 м/с. Определите:
1. продолжительность полета тела до точек А и В (рис. 1.8);
2. максимальную высоту, на которую поднимается тело;
3. дальность полета тела. Сопротивление воздуха не учитывать.

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

дано: Н=12 м.; °; ;

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

найти: a. ;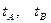

b. y_max;

с. х_max;

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

решение:

 

→→→ В обозначении на рисунке 1.8 системе координат проекции начальной скорости

 

v_0x = v₀ cos (1)

 

v_0y = v₀ sin (2)

 

Координаты тела с течением времени изменяются в соответствии с уравнение для равнопеременного движения:

 

y = H + v₀ t sin -gt²/2 (3)

 

x = v₀ tcos (4)

 

Время подъема тела найдем из условия, что в наивысшей точке подъема тела его скорость

 

v_y = v₀ sin -gt = 0 (2)

 

тогда

 

t_под = v₀ sin /g (5)

 

Время спуска тела от С до точки А равно времени подъема, поэтому продолжительность полета тела от точки О₁ до точки А равна

 

t_A = 2t _под = 2v₀sin /g (6)

 

Максимальную высоту подъема найдем из уравнения (3), подставив в него время подъема из уравнения (5)

 

y_max = H + sin² /(2g) (7)

 

Время полета тела до точки В найдем из уравнения (3), приравняв координату у нулю (y = 0)

 

(8)

 

 

Дальность полета найдем из уравнения (4), подставив в него время движения из уравнения (8)

 

x_max = v₀ t_B cos

 

вычисления

 

;

 

;

 

;

 

;

 

Ответ: a. t_А=1,22 с; t_B = 2,29 с;

b. y_max = 13,84 м;

с. x_max = 23,8 м

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

1. По условию задачи 1 найдите в момент приземления тела следующие величины:
1. Скорость падения
2. Угол падения тела
3. Тангенциальное и нормальное ускорение тела
4. Радиус кривизны траектории

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

дано: Н =12м, 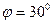, v₀=12 м/с

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

найти: a. v_B

b.

c. ,

d. R

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

решение:

→→→ Результирующая или мгновенная скорость в точке B (рис. 1.9) . Проекцию скорости v_y в точке B найдем из уравнения (2`) задачи (1), подставив в него время движения t_B [см. (8)]:

 

;

 

;

 

;

Из рис 1.8 определим угол , образуемый вектором скорости v_B с осью Ox:

;

 

; ;

 

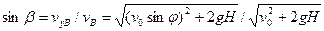Построим в точке B «треугольник ускорений». Вектор тангенциального ускорения направлен вдоль вектора мгновенной скорости в данной точке, т.е. по касательной к траектории; вектор нормального ускорения перпендикулярен вектору мгновенной скорости v_B. Из рис. 1.9 \видно, что

 

;

 

;

 

Радиус кривизны траектории в точке приземления определяем из уравнения

 

.

 

вычисления:

 

Ответ: a. v_B =19,5м/с

b.

c.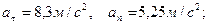

d. R =72,5 м/с²

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

1. Движение тела массой 1 кг задано уравнением s=6t²+3t+2. Найдите зависимость от времени:
1. Скорости
2. Ускорения

Вычислите силу действующую на тело в конце второй секунды.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

→→→ Мгновенную скорость находим как производную от пути по времени:

 

v=ds/dt; v=18t²+3

 

Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени:

 

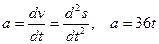
Сила, действующая на тело, определяется по второму закону Ньютона: F= ma, где согласно условию задачи a – ускорение в конце второй секунды. Тогда

 

вычисления:

Ответ: a. v=18t²+3

b. a=36t

c. F=72Н

Задачи для самоподготовки

1. От самолета, летящего горизонтально со скоростью 500 м/с, сброшен предмет. Чему равны нормальное и тангенциальное ускорения предмета через 50 с после начала падения? Сопротивление воздуха не учитывать
2. Тело брошено со скоростью 15 м/с под углом 30⁰ к горизонту. Определите:
1. Наибольшую высоту подъема
2. Дальность полета
3. Радиус кривизны траектории в наивысшей точки
3. По условию предыдущей задачи определите скорость тела, а так же его нормальное и тангенциальное ускорение через 2 с после начала движения
4. Зависимость пройденного телом пути от времени имеет вид s=2t-3t²+t³. Найдите зависимость скорости от времени и силу действующую на тело в конце второй секунды. Масса тела 1 кг
5. Материальная точка массой 1г движется по окружности радиусом 2м согласно уравнению s=8t-0,2t³. Найдите:
1. Скорость
2. Тангенциальное, нормальное и полное ускорение в момент времени 3с
6. Тело вращения равноускоренно с начальной угловой скоростью 5 с^-1 и угловым ускорением 1с^-2. Сколько оборотов сделает тело за 10 с.
7. Тело массой 2кг движется прямолинейно со скоростью, зависимость которой от времени выражается уравнением v=2,5t²+10t. Определите:
1. Пут пройденный телом за 5 с.
2. Силу, действующую на тело в конце 5 секунды
8. Найдите закон движения тела массой m под действием постоянной силы F, если в момент t=0 начальная координата x=0 и v=v₀
9. Тело массой 2кг движется с ускорением, изменяющемся по закону a=5t-10. Определите:
1. Силу, действующую на тело через 5 с после начала действия
2. Скорость в конце пятой секунды
10. Под действием постоянной силы 10 Н тело движется прямолинейно и зависимость пройденного пути от времени имеет вид s=10-5t+2t². Найдите массу тела.
11. Найдите закон движения тела массой m под действием постоянной силы F, если в момент t=0 имеем x=x₀ и v=v₀.

ГЛАВА 3 РАБОТА И ЭНЕРГИЯ

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: