Глава 4 механика твердого тела

 

Момент силы. Момент инерции

 

Момент силы

 

В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические вели­чины — момент сил и момент инерции, физический смысл которых рас­крыт ниже.

Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси 00' (рис. 1.14).

Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, назы­вают плечом силы. Произведение силы на плечо определяет модуль мо­мента силы относительно точки О:

 

 

Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:

 

(1.46)

 

v Единица момента силы — ньютон-метр (Н • м).

 

Направление М можно найти с помощью пра­вила правого винта

 

Момент инерции

 

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, назы­ваемая моментом инерции тела относительно оси вращения.

ü Момент инерции материальной точки относительно оси вращения – произведение массы этой точки на квадрат расстояния от оси:

 

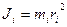(1.47)

 

ü Момент инерции тела относительно оси вращения — сумма мо­ментов инерции материальных точек, из которых состоит это тел:

 

(1.48)

 

В общем случае, если тело сплошное и представляет собой совокуп­ность точек с малыми массами dm, момент инерции определяется интег­рированием:

 

(1.49)

 

[r – расстояние от оси вращения до элемента массой dm]

Если тело однородно и его плотность , то момент инерции тела, то момент инерции тела

 

(1.50)

ü Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Наиболее просто определяется момент инерции тел, имеющих пра­вильную геометрическую форму и равномерное распределение массы по объему.

ü Момент инерции однородного стержня относительно оси, прохо­дящей через центр инерции и перпендикулярной стержню,

 

(1.51)

 

ü Момент инерции однородного цилиндра относительно оси, перпен­дикулярной его основанию и проходящей через центр инерции,

 

(1.52)

 

ü Момент инерции тонкостенного цилиндраили обруча относи­тельно оси, перпендикулярной плоскости его основания и проходящей через его центр,

 

(1.53)

ü Момент инерции шара относительно диаметра

 

(1.54)

Рассмотрим пример. Определим момент инерции диска относительно оси, проходящей че­рез центр инерции и перпендикулярной плоско­сти вращения. Масса диска — m, радиус — R.

Площадь кольца (рис. 1.15), заключенного между r и r + dr, равна 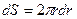. Площадь диска . Следовательно, . Тогда

или

Согласно (1.49)

 

 

Теорема Штейнера

 

Приведенные формулы для моментов инерции тел даны при усло­вии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует восполь­зоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J₀ отно­сительно оси, параллельной данной и проходящей через центр инер­ции тела, и величины md²:

 

(1.55)

 

[ m — масса тела, d — расстояние от центра масс до выбранной оси вра­щения].

 

v Единица момента инерции — килограмм-метр в квадрате (кг • м²).

 

Так, момент инерции однородного стержня относительно оси, про­ходящей через его конец, по теореме Штейнера равен

 

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: