Связь между потенциальной энергией

 

Потенциальная энергия — это функция, определяемая с точностью до некоторой произвольной постоянной. Эта произвольная постоянная одинакова для всех точек поля, а так как при всех вычислениях играет роль разность потенциальных энергий, то значение произвольной посто­янной несущественно, поэтому в приведенных выше выражениях она отсутствует. В классической механике взаимодействие частицы с окру­жающими телами описывают с помощью сил или с помощью потенци­альной энергии. Согласно (1.69), имеем

 

 

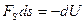
Из этой формулы следует, что связь между потенциальной энергией и силой поля имеет вид

 

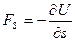(1.70)

 

Символ частной производной 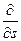свидетельствует о том, что производ­итная берется по определенному направлению. В общем случае потенци­альная энергия является функцией аргументов х, у, z, т. е. U(x, у, х). В этом случае в декартовой системе координат определяют проекции вектора F на оси X, Y, Z, тогда

 

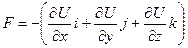(1.71)

 

[i, j, k — единичные ортогональные векторы].

Величина, стоящая в скобках, является градиентом скалярной функции.

Выражение (1.71) можно переписать в виде

 

(1.71`)

 

т.е. сила F поля равна минус градиенту потенциальной энергии.

 

 

Характеристики поля – напряженность и потенциал

 

Напряженность поля

 

Основными характеристиками любого потенциального поля в каж­дой его точке являются напряженность Е и потенциал .

Напряженность — силовая характеристика поля, величина вектор­ная. Например, под напряженностью гравитационного поля понимают силу, действующую в данной точке поля на тело единичной массы:

 

(1.72)

 

Векторы напряженности и силы совпадают по направлению.

В гравитационном поле на тела действуют силы, пропорциональные массе тел:

 

F = 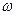g

 

или в скалярной форме

F = mg

откуда

 

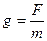(1.73)

 

т. е. отношение силы, действующей на тело массой т в какой-либо точке поля, к массе тела определяет ускорение свободного падения в данной точке поля. Сравнивая формулы (1.68) и (1.73), получаем

 

(1.74)

 

[Rз — радиус поверхности Земли, масса которой М; h — расстояние от центра тяжести тела до поверхности Земли].

Из этой формулы вытекает, что, во-первых, ускорение свободного падения не зависит от массы и размеров тела и, во-вторых, изменяется с высотой h поднятия тела над поверхностью Земли.

 

Потенциал поля

 

Это его энергетическая характеристика, величина скалярная. Потен­циал поля, например гравитационного, определяется потенциальной энергией тела единичной массы в данной точке поля:

 

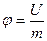(1.75)

или потенциал определяется работой по перемещению единичной массы из данной точки поля в бесконечность.

Вычислим работу, совершаемую силами поля тяготения при удале­нии тела массой т от Земли.

При перемещении этого тела на расстоянии 6R совершается работа

 

, но

 

поэтому

 

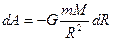(1.76)

 

[ M – масса земли]

Сила и перемещение в данном случае противоположны по направлению, поэтому в формуле (1.76) появляется знак минус.

При перемещении тела от R₁ до R₂ совершается работа

 

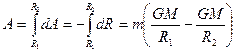(1.77)

 

Сравнивая (1.69) и (1.77), получаем

 

,

 

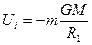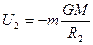
Если точка поля находится в бесконечности 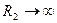, то

 

 

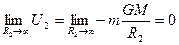
тогда (1.77) можно записать в виде

 

 

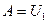
Так как первая точка была выбрана произвольно, то потенциальная энер­гия тела массой т в любой точке

 

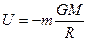(1.78)

 

Следовательно, потенциал поля тяготения

 

(1.79)

 

[ R — расстояние от центра Земли до рассматриваемой точки поля].

Геометрическое место точек с одинаковым потенциалом называ­ют эквипотенциальной поверхностью.

Из (1.79) следует, что такой поверхностью является сфера (R = = const).

Между силовой (Е) и энергетической () характеристиками потен­циального поля существует связь:

 

или

 

[s — расстояние от источника центральной силы до рассматриваемой точки поля].

 

Таким образом, напряженность поля в данной точке равна минус градиенту потенциала:

 

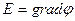(1.80)

 

Знак минус указывает, что вектор напряженности направлен в сто­рону убывания потенциала. Формула (1.80) является следствием форму­лы (1.71).

Из потенциальности поля следует, что циркуляция вектора напря­женности по любому замкнутому контуру всегда равна нулю (рис. 1.18):

 

 

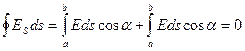
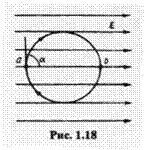т.к.

 

 

 

 

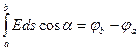
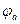[ и 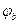- потенциал точек A и B, т.е. ]

 

 

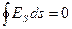Принцип суперпозиции

 

Если поле создано несколькими источниками, то результирующая напряженность поля в любой его точке определяется по принципу супер­позиции (наложения) полей:

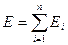(1.82)

 

Так как потенциал поля — величина скалярная, то результирующее значение потенциала определяется простым сложением:

 

(1.83)

Потенциальная энергия и работа сил поля могут быть определены через потенциал точек поля:

 

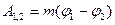, (1.84)

 

⇐ Предыдущая12345678

Поделиться:

Воспользуйтесь поиском по сайту: