Закон сохранения момента импульса

 

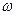При вращательном движении тела каждая его частица движется с линейной скоростью [r_i — радиус окружности, которую описыва­ет частица массой m_i, — угловая скорость, одинаковая для всех точек тела]. Момент импульса частицы .

Момент импульса вращающегося тела равен сумме моментов импульсов отдельных его частиц:

 

(1.65)

 

v Единица момента силы - -метр в квадрате (кг • м²/с).

 

Момент импульса — вектор, совпадающий по направлению с век­тором угловой скорости.

Изменение момента импульса равно импульсу момента сил:

 

 

Если суммарный момент всех внешних сил, действующих на систе­му тела относительно произвольной неподвижной оси, равен нулю, т. е. M=0, то dL=0 и векторная сумма моментов импульсов тел системы не изменяется с течением времени.

Сумма моментов импульсов всех тел изолированной системы сохраняется неизменной {закон сохранения момента импульса):

 

, (1.66)

 

Допустим, что у вращающегося тела вследствие каких-либо причин происходит увеличение момента инерции, что приводит к уменьшению угловой скорости.

Согласно выражению (1.66), можно записать 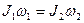где J₁ и 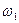— момент инерции и угловая скорость в начальный момент времени, J₂ и — в момент времени t.

Закон сохранения момента импульса связан с однородностью и изо­тропностью пространства, т. е. этот закон можно получить из второго закона Ньютона, если к нему добавить соответствующие свойства сим­метрии пространства. Под однородностью пространства понимают рав­ноправность всех точек пространства. Под изотропностью пространст­ва понимают равноправность всех направлений в пространстве. Про­странство как таковое не может изменить импульс из-за отсутствия вы­деленных в пространстве точек в силу их равноправия. Изменение им­пульса (и момента импульса) всегда связано с силой, т. е. с взаимодейст­вием тел.

 

Задачи

 

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

27. Тонкий стержень массой 300 г и длиной 50 см вращается с угловой ско­ростью 10 с^-1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Найдите угловую скорость, если в процессе вращения в той же плоскости стержень переместится так, что ось вращения пройдет через конец стержня.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Дано: m = 300 г = 0,3 кг; l = 50 см = 0,5 м; 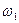= 10 с^-1

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Найти:

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

решение:

→→→ Используем закон сохранения момента импульса

 

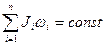(1)

 

[J₁ — момент инерции стержня относительно оси вращения].

 

Для изолированной системы тел векторная сумма моментов импульса оста­ется постоянной. Вследствие того, что распределение массы стержня относитель­но оси вращения изменяется, момент инерции стержня также изменится в соот­ветствии с (1):

 

(2)

 

Известно, что момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню, равен

 

(3)

 

По теореме Штейнера

 

 

[ J — момент инерции тела относительно произвольной оси вращения; J₀ — мо­мент инерции относительно параллельной оси, проходящей через центр масс; d — расстояние от центра масс до выбранной оси вращения].

Найдем момент инерции относительно оси, проходящей через его конец и перпендикулярной стержню:

 

, (4)

 

Подставим формулы (3) и (4) в (2):

 

 

откуда

 

 

вычисления:

 

 

Ответ: =

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

28. Маховик массой 4 кг свободно вращается с частотой 720 мин^-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика можно считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с под дейст­вием тормозящего момента маховик остановился. Найдите:

a. тормозящий мо­мент;

b. число оборотов, которое сделает маховик до полной остановки.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Дано: 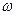=0; m = 4 кг; n = 720 мин~' = 12; 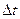= 30 с; R = 0,4 м.

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

Найти: a. M

b. N

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

решение:

→→→ Для определения тормозящего момента М сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения:

 

(1)

 

[J— момент инерции маховика относительно оси, проходящей через центр масс; — изменение угловой скорости за промежуток времени 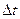]. По условию задачи

 

 

[ — начальная угловая скорость, так как конечная угловая скорость 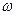= 0].

 

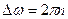Выразим начальную угловую скорость через частоту вращения маховика, тогда и . Момент инерции маховика

 

 

[m — масса маховика; R — его радиус].

 

 

Тогда формула (1) примет вид , откуда

 

 

Угол поворота, т. е. угловой путь <р, за время вращения маховика до оста­новки может быть определен по формуле для равнозамедленного вращения:

 

(2)

 

[ — угловое ускорение].

 

По условию задачи, Тогда [см.(2)]

 

т.к. 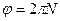, , то число полных оборотов

 

 

Вычисления:

 

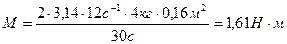
Ответ: a. M=1,61 Hм

b. N=180

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

 

Задачи для самоподготовки

29. Сплошной цилиндр массой 10 кг катится без скольжения с постоянной скоростью 10 м/с. Определите:

a. кинетическую энергию цилиндра;

b. время до его остановки, если на него действует сила трения 50 Н.

30. Сплошной шар скатывается по наклонной плоскости, длина которой 10 м и угол наклона 30° Определите скорость шара в конце наклонной плоскости. Трение шара о плоскость не учитывать.

31. Полый цилиндр массой 2 кг катится по горизонтальной поверхности со скоростью 20 м/с. Определите силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6 м.

32. Маховик, имеющий форму диска массой 30 кг и радиусом 10 см, был раскручен до частоты 300 мин^-1. Под действием силы трения диск остановился через 20 с. Найдите момент сил трения, считая его постоянным.

33. Шар и сплошной цилиндр имеют одинаковую массу 5 кг каждый и ка­тятся с одинаковой скоростью 10 м/с. Найдите кинетическую энергию этих тел.

 

 

34. Сплошной шар массой 1 кг и радиусом 5 см вращается вокруг оси, про­ходящей через его центр. Закон вращения шара выражается уравнением . В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Определите:

a. эту силу;

b. тормозящий мо­мент.

35. Какой скоростью должен обладать шар, катящийся без скольжения, что­бы подняться по наклонной плоскости, составляющей с горизонтом угол 30°, на высоту 2 м, если сила трения равна 0,2 силы давления шара на плоскость? Чему равно время подъема?

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: