Основные положения теории случайных погрешностей. Распределение Гаусса

В основе теории случайных погрешностей лежит теория вероятностей и методы математической статистики. Из этого следует, что точный расчет погрешностей невозможен. Оценку случайной погрешности и определение интервала, внутри которого с заданной вероятностью лежит истинное значение физической величины, проводят по результатам ее многократных измерений.

В дальнейшем будем предполагать, что:

– грубые погрешности исключены;

– поправки, которые следовало определить (например, смещение нулевого деления шкалы), вычислены и внесены в окончательные результаты;

– все систематические погрешности известны (с точностью до знака).

В этом случае результаты измерений все же оказываются не свободными от случайных погрешностей. Если случайная погрешность окажется меньше систематической, то очевидно, нет смысла пытаться уменьшить величину случайной погрешности. На практике обычно уменьшают случайную погрешность до тех пор, пока она не станет сравнимой по величине с систематической погрешностью.

Случайные погрешности результатов эксперимента можно рассматривать как разновидность случайных величин (событий), т.е. переменных величин, значения которых зависят от случая. Свойства большого количества случайных величин изучаются теорией вероятности, основным понятием которой является вероятность –числовая характеристика возможности появления некоторого определенного события в цепи событий, которые могут повторяться неограниченное число раз. Приближенной характеристикой вероятности случайного события является относительная частота – отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события определяется формулой

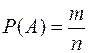, (2.1)

где – число появлений события, 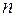– общее число испытаний.

Если число испытаний достаточно велико, то относительная частота изменяется мало, колеблясь около некоторого постоянного числа, являющегося вероятностью появления события. Т.е. вероятность события есть предельное значение частоты его появления при бесконечном числе испытаний.

Допустим, что сделано 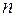повторных измерений одной и той же величины. Если они выполнены одним и тем же методом, в одинаковых условиях и с одинаковой степенью тщательности, то такие измерения называются равноточными.

Пусть минимальный интервал значений измеряемой величины, через который ведутся отсчеты (цена деления прибора), будет , а среднее значение всех результатов измерений пусть будет . Обозначим через число тех результатов, которые отклонились от среднего на величину . Отложив по оси абсцисс величину абсолютных погрешностей , а по оси ординат значения 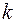, получим ступенчатый график, называемый гистограммой (рис. 1).

Если устремить число измерений к бесконечности, а интервал – к нулю, то гистограмма переходит в пределе в непрерывную функцию, которая является кривой распределения погрешностей. При некоторых условиях, которые обычно выполняются при проведении измерений, эта кривая представляет собой график функции Гаусса, имеющий следующий вид

, (2.2)

где параметр 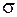определяет ширину распределения. Несколько кривых Гаусса для разных значений параметра 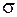показаны на рис. 2.

Максимум кривой распределения называется математическим ожиданием и соответствует истинному значению измеряемой величины , которое можно получить, произведя усреднение по функции распределения

. (2.3)

При большом числе измерений () среднее значение будет с стремиться к величине математического ожидания.