Точность записи результатов измерений и правила округлений

Когда все измерения, необходимые для данного физического эксперимента закончены, предстоит сделать на основании их значений вычисления искомой величины. При вычислениях на микрокалькуляторе в ответе автоматически получается столько цифр, сколько их вмещается на индикаторе микрокалькулятора. При этом создается впечатление от избыточной точности результата. В то же время результаты измерений являются приближенными числами. Напомним, что для приближенных чисел отличают запись 2,4 от 2,40 или 0,02 от 0,0200 и т.д. Запись 2,4 означает, что верны только цифры целых и десятых истинное же значение числа может быть, например, 2,43 или 2,38. То же отличие проводится и для целых чисел. Запись 382 означает, что все цифры верны. Если же за последнюю цифру ручаться нельзя, то число округляется, но записывается не в виде 380, в виде 38·10. Запись же 380 означает, что последняя цифра (ноль) верна. Если в числе 1730 верны лишь первые две цифры, его нужно записать в виде 17·10² или 1,7·10³. В тех случаях, когда численные значения физических величин много меньше либо много больше единицы, их принято записывать в виде числа между 1 и 10, умноженного на соответствующую степень десяти, например: 1,6·10^–19 или 3·10⁸.

Пример 1. 0,00508 – в этом числе имеются три значащих цифры: 5, ноль между 5 и 8, и 8, первые три нуля незначащие.

В числе 7,13·10³ – три значащих цифры – 7, 1, 3.

Пример 2. Записи 12,7 и 12,700 различны! Запись 12,700 означает, что верны десятые, сотые и тысячные доли. В записи 12,7 – верны целые и десятые доли.

Число знаков в окончательном результате устанавливается по следующим правилам:

1. Сначала ограничивается число значащих цифр погрешности. Значащими цифрами называются все верные цифры кроме нулей, стоящих впереди числа.

2. Погрешность записывается всегда с одной или двумя значащими цифрами (запись двух значащих цифр предполагает высокую точность измерений).

3. Число цифр в результатах промежуточных расчетов обычно должно быть на одну больше, чем в окончательном результате. Погрешности при промежуточных вычислениях должны быть выражены не более чем тремя значащими цифрами.

После того, как погрешность записана, значение результата должно быть округлено таким образом, чтобы его последняя значащая цифра была того же разряда, что и у погрешности.

Пример 3. Правильное представление окончательного результата: 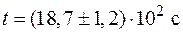, , 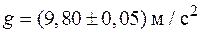при этом необходимо указывать единицы измерений физической величины.

Округление погрешностей и результаты измерений самой физической величины производят по следующим общепринятым правилам:

1. Округление результата измерения достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше пяти.

Пример 4. 4,32 (округлить до десятых) ≈ 4,3

5,331 (округлить до сотых) ≈ 5,33

6,432 (округлить до целых) ≈ 6

2. Если первая из отбрасываемых цифр больше 5, то последняя оставляемая цифра увеличивается на единицу.

Пример 5. различные округления числа 39,867 будут: 39,87; 39,9 и 40.

3. Если отбрасываемая цифра равна 5, то стоящая перед ней нечетная цифра увеличивается на единицу, а четная остается неизменной.

Пример 6. 0,435 (округлить до сотых) ≈ 0,44

0,5450 (округлить до сотых) ≈ 0,54

345,521 (округлить до целых) ≈ 346

346,521 (округлить до целых) ≈ 346

4. При сложении и вычитании округление всех чисел производится по вышеуказанным правилам. В окончательном результате следует сохранить столько знаков, сколько их в том из рабочих чисел, в котором наименьшее число десятичных знаков, причем, в промежуточном вычислении желательно оставлять запасной знак.

Пример 7.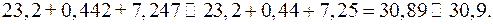

При умножении и делении соблюдаются те же правила . При возведении в степень или извлечения корня в конечном результате следует сохранить столько значащих цифр, сколько их имеет возводимое в степень или подкоренное приближенное число.

Пример 8.

.

 

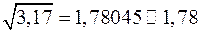Построение графиков

В лабораторном практикуме и при выполнении расчетно-графических (семестровых) работ по физике часто возникает необходимость построения графических зависимостей. При оформлении графиков нужно следовать нижеперечисленным правилам.

1. Графики строят на миллиметровой бумаге форматом не менее чем 14´16 мм (страница стандартной тетради). Готовый график должен быть подклеен к отчету по лабораторной работе. В виде исключения допускается построение зависимостей с помощью стандартных компьютерных программ – но и в этом случае графики должны соответствовать всем изложенным здесь требованиям (в частности, иметь масштабно-координатную сетку).

2. На координатных осях должны быть указаны обозначения откладываемых величин и единицы их измерения.

3. Начало координат, если это не оговорено особо, может не совпадать с нулевыми значениями величин. Его выбирают таким образом, чтобы площадь чертежа была использована максимально.

4. Экспериментальные точки изображаются четко и крупно: в виде кружков, крестиков и т.п.

5. Масштабные деления на координатных осях следует наносить равномерно. Координаты экспериментальных точек на осях не указывают, а линии, определяющие эти координаты, не проводят.

6. Масштаб выбирают таким образом, чтобы:

а) кривая была равномерно растянута вдоль обеих осей (если график представляет собой прямую, то угол ее наклона к осям должен быть близок к 45°);

б) положение любой точки можно было определить легко и быстро (масштаб, при котором чтение графика затруднено, считается неприемлемым*).

7. Если наблюдается значительный разброс экспериментальных точек, то кривую (прямую) следует проводить не по точкам, а между ними – так, чтобы количество точек по обе стороны от нее было одинаковым. Кривая должна быть плавной.

 

Пример 1. Пусть требуется построить график зависимости пути S от времени t при равномерном движении тела. Экспериментальные данные приведены в табл. 6. Два варианта графика зависимости S (t) – оформленный с ошибками и правильный – изображены на рис. 4 и 5.

 

Таблица 6

 

t, c
S, м

 

Основные, наиболее типичные ошибки, допускаемые студентами при построении графиков (рис. 4):

– неправильно выбраны направления осей координат: время t является независимой переменной (аргументом) и должно быть отложено по оси абсцисс (горизонтальной), а зависимая переменная (функция) – путь S – по оси ординат (вертикальной);

– на оси ординат не указаны отложенная величина (время t) и единицы ее измерения (с), а на оси абсцисс – единицы измерения пути S (м) – см. п. 2;

*Масштаб является удобным для чтения графика, если в единице, отложенной по оси величины содержится одна (или две, пять, десять, двадцать, пятьдесят и т.д.) линейная единица – миллиметр или сантиметр. Следует избегать неудобного, но часто используемого студентами масштаба – 15 или 30 мм на единицу величины.

– площадь чертежа использована не полностью (поскольку из условия примера не следует, что оси координат должны начинаться с нулевых значений, то начало координат следует сместить и за счет этого увеличить масштаб графика) – см. п. 3;

– не выделены экспериментальные точки – п. 4;

– масштабные деления на оси времени нанесены неравномерно (если есть деления 0 и 5, то следующим должно быть 10 и т.д.) – п. 5;

– на оси пути нанесены не масштабные деления, а координаты экспериментальных точек; проведены лишние пунктирные линии – см. также п. 5;

– график сжат по оси абсцисс за счет двух причин: неправильно выбранного начала координат (п. 3) и неудачного (слишком мелкого) масштаба – п. 6, а;

– выбран крайне неудобный масштаб по времени, в связи с чем чтение графика затруднено – п. 6, б;

– неправильно соединены экспериментальные точки: зависимость пути от времени при равномерном движении заведомо линейна, и график должен представлять собой прямую – п. 7.

 

Правильно оформленный график представлен на рис. 5.

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: