Оценка случайных погрешностей косвенных измерений

В большинстве случаев искомая физическая величина является функцией одной или нескольких измеряемых величин. Для определения такой величины необходимо провести ряд непосредственных (прямых) измерений вспомогательных величин, а затем, используя функциональную зависимость, вычислить искомую величину. Зная ошибки, допущенные при прямых измерениях, и точность, с которой взяты табличные значения физических постоянных, можно найти возможную ошибку косвенных измерений. В таблице 5 приведены формулы для вычисления погрешностей результатов алгебраических действий. Формулы для нахождения ошибок выведены в предложении, что ошибки всех исходных данных малы по сравнению с самими величинами, и поэтому произведениями, квадратами и более высокими степенями ошибок можно пренебречь, как величинами более высоких порядков малости. Кроме того, при расчетах ошибок предполагается самое неблагоприятное сочетание знаков ошибок исходных данных, т.е. определяют величину предельной ошибки измерения (погрешности только складываются!).

Однако при сложной зависимости между физическими величинами можно пользоваться не готовыми формулами таблицы, а дифференциальным или логарифмическим методом нахождения ошибок.

Какому из методов отдать предпочтение – зависит от вида функциональной зависимости измеряемых величин. Если зависимость измеряемых величин представлена в виде слагаемых (или разности), то применяют дифференциальный метод, а если – произведение (или частное) измеряемых величин, то применяют логарифмический метод.

Таблица 5

Формулы для вычисления погрешностей

результатов алгебраических действий и некоторых функций

№	Математи-ческая операция	Абсолютная ошибка	Относительная ошибка
1.
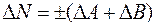
2.
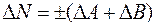
3.
4.
5.
6.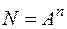
7.
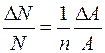
8.
9.
10.
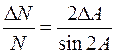
11.
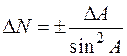
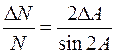
12.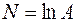
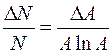
13.

Дифференциальный метод

Известно, что дифференциал функции есть ее малое приращение при малом приращении аргумента, и он мал по сравнению с самой функцией. Приближенно можно считать, что функция и ее дифференциал находятся в том же отношении, как и измеряемая величина с абсолютной ошибкой. Это позволяет использовать дифференциальное исчисление для расчета абсолютной и относительной ошибок.

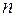Рассмотрим, каким образом оценить случайную погрешность косвенно измеряемой величины , которая является функцией некоторого числа непосредственно измеряемых величин 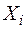, т.е.

. (4.1)

Среднее значение можно найти из известной функциональной зависимости (4.1), подставляя в качестве аргументов усредненное по всем проведенным опытам значения непосредственно измеряемых величин 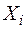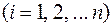. Согласно правилам дифференцирования дифференциал функции имеет вид

. (4.2)

где 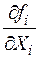– частная производная функции по переменной .

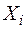Таким образом, приращение функции равно сумме частных производных этой функции на приращение аргумента. Тогда абсолютную ошибку можно находить с помощью полного дифференциала функции .

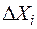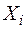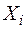Каждый из частных дифференциалов определяет ту часть ошибки в величине функции, которая возникает из-за ошибки одной из переменных . При вычислении частной производной все аргументы, кроме , считаются постоянными, а дифференцирование по переменной 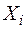производят по правилам функции одного переменного. Для того, чтобы быть уверенным, что при самом неблагоприятном сочетании знаков ошибок аргумента 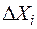, ошибка функции не выходит за пределы , необходимо найти максимальное значение . Такое максимальное (предельное) значение ошибки получится в том случае, когда все слагаемые суммы

(4.3)

положительны, т.е.

. (4.4)

Таким образом, предельная ошибка функции нескольких независимых переменных равна сумме абсолютных величин всех частных дифференциалов этой функции, причем знак дифференциала аргумента заменяется знаком абсолютной ошибки 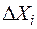. Соответствующие вычисления показывают, что абсолютная погрешность определяется по формуле

. (4.5)

Чтобы найти относительную погрешность физической величины , необходимо поделить выражение (4.5) на среднее значение .

Рассмотрим применение формул (4.4) и (4.5) на примерах.