 |
Линеаризация нелинейных зависимостей
|
|
|
|
Описанный выше графический способ, а также полученные методом наименьших квадратов формулы (7.10)-(7.12) для расчета коэффициентов в ряде случаев могут быть использованы и при обработке нелинейных зависимостей. В первую очередь это относится к зависимостям, описываемым степенными и показательными (экспоненциальными) функциями. Для их линеаризации (приведения к линейному виду) применяется операция логарифмирования.
Степенная зависимость. Пусть измеряемые величины Х и Y теоретически связаны зависимостью вида
,
где С и k – неизвестные коэффициенты. Логарифмируя данное выражение, получим
Приняв обозначения
придем к зависимости вида (7.2). После определения коэффициентов K и b одним из описанных выше способов, найдем параметры исходной зависимости:
Экспоненциальная зависимость. Многие физические явления и процессы (движение тела в вязкой среде, затухающие колебания, радиоактивный распад, поглощение излучения веществом и др.) описываются дифференциальными уравнениями, решение которых приводит к экспоненциальной (показательной) зависимости между физическими величинами х и Y
. (7.13)
Если коэффициенты 
и K неизвестны, но имеется экспериментально полученная зависимость Y (x), то для определения С и K ее приводят к линейному виду путем логарифмирования:
.
Положив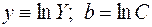 
, опять придем к зависимости вида (7.2), коэффициенты которой K и b можно найти как графическим способом, так и методом наименьших квадратов. После этого предэкспоненциальный множитель, т.е. коэффициент С исходной зависимости (7.13), определится как
С = ехр(b).
Пример 2. Зависимость сопротивления R полупроводника от его абсолютной температуры Т (лабораторная работа № 80) имеет вид
|
|
|
, (7.14)
где R 0 – константа, характеризующая сопротивление данного полупроводника при 0o C; D E – энергия активации; k – постоянная Больцмана. Путем замены переменных
и введения обозначений
,
после логарифмирования выражения (7.14) придем к линейной зависимости (7.2). Измеряя сопротивление R при различной температуре Т, одним из описанных выше способов можно найти коэффициенты K и b, а затем перейти к параметрам исходной зависимости:
.
Пример 3. При изучении явления термоэлектронной эмиссии с помощью вакуумного (лампового) диода получена зависимость плотности тока насыщения j н от температуры катода Т. Теоретически связь между этими величинами устанавливает закон Ричардсона-Дэшмена
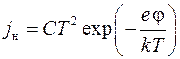, (7.15)
где С – постоянный множитель; е – элементарный заряд; j – потенциал выхода; k – постоянная Больцмана.
Для линеаризации выражения (7.15) разделим обе его части на Т 2 и прологарифмируем, в результате чего получим линейную зависимость вида (7.2) с переменными
и коэффициентами
.
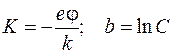После определения коэффициентов K и b неизвестные параметры исходной зависимости (7.15) можно найти как
.
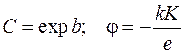Пример 4. При изучении затухающих колебаний снималась зависимость их амплитуды А от числа колебаний N. Теоретически эти величины связаны экспоненциальным законом
, (7.16)
где А 0 – начальная амплитуда; l – логарифмический декремент затухания. Для определения неизвестных параметров А 0 и l зависимости (7.16) линеаризуем последнюю по аналогии с (7.13), логарифмируя ее
и вводя обозначения
.
Коэффициенты K и b линеаризованной зависимости будем искать методом наименьших квадратов. Составим таблицу по образцу табл. 9; занесем в нее результаты измерений и соответствующих вычислений. Затем проведем расчеты по формулам (7.10)-(7.12), учитывая принятые обозначения:
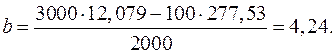
Таблица 10
| Номер опыта | N | A, мм | ln A | N 2 | N ×ln A |
| 3,784 | 37,84 | ||||
| 3,219 | 64,38 | ||||
| 2,773 | 83,19 | ||||
| 2,303 | 92,12 | ||||
| S = | 12,079 | 277,53 |
Параметры исходной зависимости (7.16):
|
|
|
На рис. 14 для наглядности изображены графики исходной (а) и линеаризованной (б) зависимостей амплитуды от числа колебаний. Кружками на графиках обозначены экспериментальные данные, сплошными линиями – результаты расчетов по найденным значениям параметров А 0 и l.
|
|
|
