 |
Пример расчета погрешности косвенного измерения дифференциальным методом
|
|
|
|
Пример 1. Пусть функциональная зависимость косвенно измеряемой величины 
от непосредственно измеряемых величин 
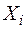имеет следующий простой вид
,
где 
– коэффициенты, 
– непосредственно измеряемые величины.
Поскольку функция представляет сумму двух слагаемых, находим частные производные:
; 
и подставляем их в формулу (4.5)
,
причем абсолютные погрешности 
и 
должны быть предварительно определены методами оценки погрешности прямых измерений. Относительную погрешность определим как
.
Пример 2. При определении ускорения движения тела без начальной скорости результаты прямых измерений и оценки их погрешностей имеют следующие значения:
расстояние, пройденное телом 
, а время 
и среднее значение ускорения найдем из функциональной зависимости 
.
Найдем частные производные из расчетной формулы
; 
.
Тогда выражение для расчета абсолютной погрешности ускорения имеет вид
.
Вместо 
и 
в формулу подставляем среднее значение этих величин.
.
Окончательно результат выглядит следующим образом
; 
.
Логарифмический метод
Если формула, по которой рассчитывается физическая величина, представляет собой функцию произведений, или комбинацию произведения и частного нескольких независимых переменных, то для оценки погрешности лучше применить логарифмический метод.
Применение логарифмического метода для определения погрешности косвенных измерений логически следует из дифференциального метода. Во-первых, при логарифмировании любой функции, содержащей сомножители различных степеней, она распадается на сумму логарифмов отдельных переменных. Во-вторых, дифференциал натурального логарифма любой переменной сразу дает относительную погрешность измеряемой величины. Действительно, для функции одного переменного известно, что
|
|
|
. (4.6)
Правая часть выражения (4.6) приближенно равна относительной ошибке 
. Это позволяет достаточно просто определить величину относительной ошибки по формуле (заменив 
на 
)
. (4.7)
Для вычисления относительной ошибки функции нескольких переменных, как и в случае одного переменного, воспользуемся формулой
. (4.8)
Откуда предельная относительная ошибка функции нескольких переменных равна сумме абсолютных величин частных дифференциалов натурального логарифма этой функции:
, (4.9)
(4.10)
более строго выражение (4.10) можно записать как
, (4.11)
где вместо необходимо подставить среднее значение 
, вычисленное их функциональной зависимости физической величины от непосредственных переменных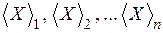 
. Учитывая простую связь между абсолютной и относительной погрешностями 
, легко по известной величине 
вычислить 
, и наоборот.
Таким образом, последовательность действий при расчетах погрешности логарифмическим методом состоит в следующем:
1. Функция 
, используемая для вычисления изучаемой величины, сначала логарифмируется.
2. Выражение, полученное после логарифмирования, дифференцируется (берется производная).
3. Знак «
» следует заменить на знак «
», и каждый дифференциал берется по абсолютной величине, т.е. все «минусы» перед абсолютными ошибками непосредственно измеренных величин заменяются на «плюсы». Рассмотрим применение логарифмического метода на примерах.
Пример 1. Пусть функциональная зависимость косвенно измеряемой величины от непосредственно измеряемых величин 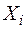имеет следующий вид
.
Найдем логарифм выражения
,
определим частные производные
; 
; 
,
подставляя в (4.10), и заменяя «минусы» на плюсы, получим
,
вместо , 
, 
подставляем их среднее значение. Зная относительную погрешность нетрудно вычислить и абсолютную ошибку
|
|
|
.
Пример 2. Момент инерции круглой платформы, подвешенной на трифилярном подвесе, рассчитывается по формуле
,
где 
– радиус платформы, 
– радиус верхнего диска подвеса,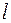 
– длина нитей подвеса, 
– масса платформы, 
– период малых колебаний платформы, 
– ускорение свободного падения, 
(отношение длины окружности к диаметру).
Найдем относительную ошибку, а затем абсолютную для момента инерции 
. Выражение для удобно для логарифмирования. Для нахождения ошибок выполним следующие операции:
1. Логарифмирование
.
2. Дифференцирование
.
3. Заменяем знак «» на знак «», и знаки «минусы» на «плюсы».
.
В эту формулу надо подставить численные значения относительных ошибок величин 
. Значения 
и их абсолютные ошибки 
даны как постоянные прибора. Период колебаний и 
определяются на опыте. Точность значений и 
следует брать из таблиц справочников физических величин, с числом значащих цифр, равным числу последних из экспериментальных данных. Зная относительную ошибку, легко рассчитать абсолютную ошибку измеряемой величины
.
|
|
|
