 |
Обработка экспериментальных зависимостей
|
|
|
|
Определение коэффициентов линейной зависимости
Часто в практике физического эксперимента искомую величину невозможно определить из опытов, проведенных в одних и тех же условиях. Например, в лабораторной работе № 3 требуется найти момент инерции J крестовины маятника Обербека. С этой целью измеряются момент М н силы натяжения нити и угловое ускорение e крестовины. Связь между этими величинами устанавливает основной закон динамики вращательного движения, уравнение которого в данном случае имеет вид
, (7.1)
где М тр – момент сил трения. Очевидно, что сколько бы опытов при одном и том же значении М н ни проводилось, из формулы (7.1) нельзя найти момент инерции J, так как величина момента сил трения также неизвестна.
Введем обозначения:
,
с учетом которых выражение (7.1) приводится к стандартному виду линейной зависимости
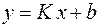, (7.2)
коэффициенты которой K и b неизвестны.
Формально для нахождения K и b достаточно измерить два значения функции y 1 и y 2 при различных значениях аргумента х 1 и х 2. Подстановка этих значений в (7.2) позволяет получить систему двух независимых уравнений для определения неизвестных коэффициентов:
Решая систему, находим:
; (7.3)
.
Этот метод дает возможность получить лишь грубую оценку коэффициентов, так как величины х и у измеряются с погрешностями.
Учесть наличие погрешностей и найти некоторые осредненные значения K и b можно только путем неоднократного измерения величины у при различных х. В дальнейшем допустим, что в результате опытов получено п значений независимой переменной х 1, х 2, …, хп и п соответствующих им значений функции у 1, у 2, …, уп.
Графический способ
При использовании графического способа определения коэффициентов K и b экспериментальные точки наносят на график зависимости у (х), а затем проводят сглаживающую прямую (см. п. 7 правил построения графиков на с. 26). При условии, что ось абсцисс начинается с нуля, отрезок, отсекаемый этой прямой на оси 0 у, численно – с учетом масштаба – равен коэффициенту b. Тангенс угла наклона прямой к оси 0 х (опять же с учетом масштаба) дает значение коэффициента K. Для нахождения тангенса угла наклона нужно на сглаживающей прямой выбрать две точки 1и2, расположенные достаточно далеко друг от друга и определить их координаты (значения аргумента х 1 и х 2 и функции у 1 и у 2). Коэффициент K вычисляется по формуле (7.3), которую для краткости записывают в виде
|
|
|
,
где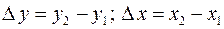 
.
Пример 1. Для определения ЭДС аккумулятора 
и его внутреннего сопротивления r были проведены измерения силы тока I в цепи источника и напряжения U на его зажимах при различной нагрузке. Экспериментальные результаты приведены в табл. 7.
Таблица 7
| I, A | 1,20 | 1,35 | 2,00 | 2,40 | 3,00 | 4,00 |
| U, B | 19,1 | 15,5 | 12,9 | 11,5 | 10,0 | 4,3 |
Теоретически, на основании закона Ома для замкнутой цепи, измеренные величины связаны соотношением
.
Сопоставляя с (7.2), имеем:
.
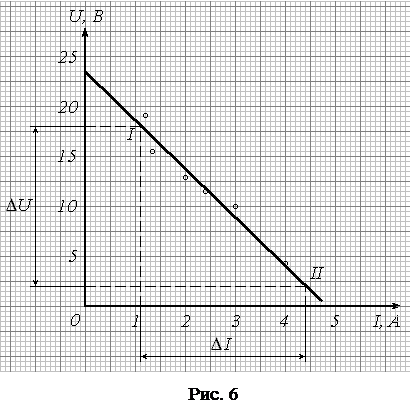
Построенный по данным табл. 7 график приведен на рис. 6. Обработка графической зависимости согласно вышеизложенным правилам дает следующие результаты:
;
.
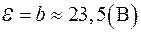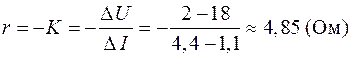На рис. 7-12 показаны наиболее распространенные ошибки, допускаемые студентами при графической обработке линейных зависимостей.
Рис. 7 иллюстрирует две типичные ошибки. Во-первых, неправильно определена величина = 22,5 В. Во-вторых, координаты точек I и II взяты не со сглаживающей прямой, а из таблицы экспериментальных данных. Поэтому величина
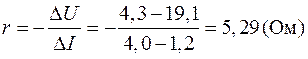
не является осредненной, и случайная погрешность ее определения может быть очень большой (при таком способе вычисления r построение графика вообще не имеет смысла).
|
|
|
На рис. 8 точки I и II выбраны слишком близко друг к другу. При малых длинах отрезков D U и D I растет относительная ошибка их измерения, а, следовательно, и погрешность определения углового коэффициента
.
На рис. 9 и 10 графики построены безукоризненно, и величина = 23,5 В найдена верно. Тем не менее, здесь допущена одна и та же грубейшая ошибка. Она заключается в том, что при определении тангенса угла наклона прямой не учтен масштаб откладываемых по осям переменных. В обоих случаях, получим результаты:
не имеющие ничего общего с искомой физической величиной и даже лишенные единиц измерения (только в том случае, когда отрезки D U и D I выражены соответственно в вольтах и амперах, их отношение будет иметь размерность Ом).Очевидно, что изменение масштаба графика приведет к изменению реального угла наклона прямой j, что при правильном определении углового коэффициента не должно влиять на получаемый результат.
Ошибки, показанные на рис. 11и 12, связаны с неудачным выбором масштаба (см. п. 6 правил построения графиков). Сжатие графика по оси ординат (рис. 11) приводит к большой погрешности измерения величин и D U; последнее отрицательно влияет на точность определения r:
= 21 B;
;
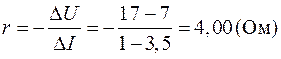сжатие по оси абсцисс (рис. 12) увеличивает ошибку измерения D I и также приводит к снижению точности нахождения обоих коэффициентов:
= 24,5B;
.
Приведенные примеры свидетельствуют о том, что графический способ определения коэффициентов линейной зависимости не свободен от недостатков. Главный из них заключается в том, что проведение сглаживающей прямой носит субъективный характер. Из этого следует, что при значительном разбросе экспериментальных данных результат осреднения коэффициентов будет неоднозначным. Как показано на рис. 13, через одни и те же точки можно провести разные прямые – например, 1, 2 и 3, – и тем самым получить различные значения искомых коэффициентов. Причем в ряде случаев полученный результат может противоречить физическому смыслу. Например, если величина х представляет собой момент силы натяжения нити М н, а у – угловое ускорение крестовины маятника Обербека (лабораторная работа № 3), то определенное по прямой 3 значение момента сил трения М тр, в соответствии с формулами (7.1) и (7.2), будет отрицательным (при этом крестовина должна начать вращение в сторону, противоположную приложенному моменту силы натяжения).
|
|
|
|
|
|
