 |
Среднеквадратичное отклонение.
|
|
|
|
Распределение Стьюдента
Для оценки случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или средней квадратичной погрешности. Средней квадратичной погрешностью называется величина
, (2.4)
где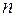 
– число измерений.
Если число измерений очень велико, то подверженная случайным колебаниям величина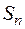 
стремится к постоянному значению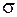 
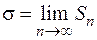. (2.5)
Именно этот предел и входит в качестве параметра 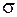в распределение Гаусса (2.2). Квадрат этой величины называется дисперсией измерений. Теория показывает, что средняя квадратичная погрешность среднего арифметического 
равна средней квадратичной погрешности отдельного результата измерений 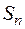деленной на корень квадратный из числа измерений 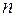, т.е.
. (2.6)
Это фундаментальный закон возрастания точности при росте числа наблюдений. Тогда
. (2.7)
средняя квадратичная ошибка 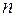– измерений. Из выражения (2.7) следует, что желая повысить точность в 2 раза, нужно вместо одного измерения сделать 4, а чтобы повысить точность в 3 раза, надо увеличить число измерений в 9 раз.
Рассмотрим некоторые операции над среднеквадратичными ошибками.
Пусть измеряемая величина 
является суммой или разностью двух величин 
и 
, результаты измерений которых независимы, т.е.
. Если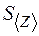 
, 
, 
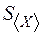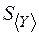– среднеквадратичные ошибки, то
. (2.8)
Это утверждение справедливо и для большого числа величин, входящих в сумму.
Если представляет собой функцию более сложную, то среднюю квадратичную ошибку результата следует находить как
, (2.9)
где 
– частная производная функции от переменных 
, 
, … 
.
Некоторые соотношения между среднеквадратичными ошибками приведены в таблице 1.
|
|
|
Таблица 1
Функциональная
связь между ,  и 
| Соотношение между среднеквадратичными ошибками |
| 
|
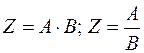
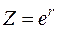
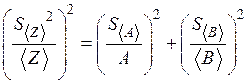
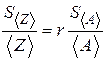
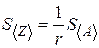
В учебных лабораториях число экспериментальных измерений ограничено 
, при этом распределение Гаусса для случайных погрешностей выполняется приближенно.
В 1908 году английским математиком Госсетом (псевдоним – Стьюдент) был предложен другой закон распределения случайных погрешностей измерений – распределение Стьюдента (используется при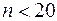 
). При 
распределение Стьюдента мало отличается от распределения Гаусса.
Распределение Стьюдента позволяет по заданной величине доверительной вероятности (надежности) 
найти границы доверительного интервала 
. Что понимают под доверительной вероятностью ?
Пусть означает вероятность того, что результат измерений отличается от истинного на величину, не большую, чем 
.
Вероятность в этом случае называется доверительной вероятностью, а интервал значений измерений величины от 
до 
называется доверительным интервалом. Определим доверительный интервал. Чем большим будет установлен этот интервал, тем с большей вероятностью истинное значение попадает в этот интервал. С другой стороны, более широкий интервал дает меньшую информацию относительного истинного значения измеряемой величины. На рис. 3 показано, что при прочих равных условиях для увеличения вероятности попадания истинного значения в доверительный интервал необходимо увеличить ширину последнего. С другой стороны, для уменьшения ширины доверительного интервала, необходимо увеличить число измерений .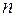
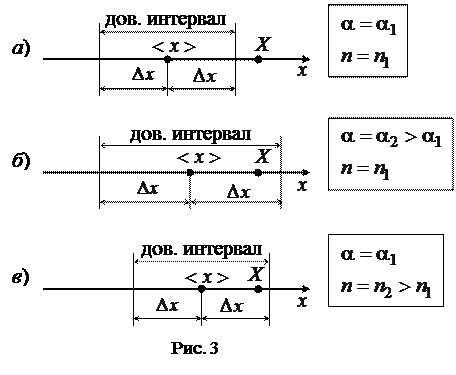
Ширина искомого доверительного интервала прямо пропорциональна среднеквадратичной ошибке
. (2.10)
Коэффициент пропорциональности 
называется коэффициентом Стьюдента: он зависит от числа опытов 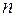и доверительной вероятности . С увеличением количества опытов среднее значение становится ближе к истинному, поэтому при той же вероятности доверительный интервал можно взять более узким (рис. 3, а, в). Таким образом, с увеличением числа измерений 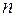коэффициент Стьюдента должен уменьшаться и при 
распределение Стьюдента переходит в распределение Гаусса.
|
|
|
Чтобы окончательно установить границы доверительного интервала необходимо расширить его с учетом систематической (приборной) погрешности 
. Обычно суммарная погрешность определяется как
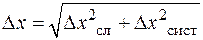. (2.11)
Истинное значение измеряемой величины заключено в интервале, определяемом средней квадратичной ошибкой 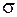с вероятностью (надежностью) 
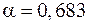(~70%). Для большинства измерений в учебных физических лабораториях выбирается: 
.
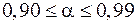В таблице приведены часто используемые значения коэффициентов Стьюдента.
Коэффициенты Стьюдента
Таблица 2
| Число измерений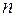
| Доверительная вероятность (надежность)
| ||
| 0,90 | 0,95 | 0,99 | |
| 6,314 2,920 2,353 2,132 2,015 1,943 1,895 1,860 1,833 | 12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 | 63,657 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 |
|
|
|
