Напряжения в наклонных сечениях при одно- и двухосном напряженных состояниях

Исследование напряженного состояния материала в точке сводится к нахождению напряжений, возникающих на наклон­ных площадках, при известных напряжениях на гранях выде­ленного элемента. Выделим элемент бруса (рис. 2.7). Пусть по двум противоположным граням возникают нормальные напря­жения σ, а остальные грани свободны от напряжений, т. е. рассмотрим случай одноосного напряженного состояния.

Найдем напряжения по некоторому наклонному сечению тп, внешняя нормаль к которому составляет с осью стержня угол а. За положительное направление отсчета угла примем направле­ние против хода часовой стрелки. Рассечем мысленно этим се­чением стержень на две части и рассмотрим равновесие одной из частей, например, нижней (рис. 2.7).

Действие отброшен­ной части стержня на оставшуюся заменим напряжениями Р, которые примем равномерно распределенными по проведенно­му сечению. Площадь наклонного сечения будет

где dA — площадь поперечного сечения элемента бруса.

Рис. 2.7

 

Для равновесия отсеченной части напряжения Р_а должны быть направлены параллельно оси стержня и уравновешивать нормаль­ную силу. Уравнение равновесия имеет вид

Отсюда

Напряжение Р_α, как известно, называется полным напряже­нием.

Раскладывая вектор Р_α в какой-либо точке наклонного сече­ния на нормальную и касательную составляющие (см. рис. 2.7), найдем составляющие полного напряжения, т. е. нормальное на­пряжение а и касательное напряжение . Подставляя в эти выражения вместо Р_α его значение по формуле (2.11), получим

Установим следующие правила знаков относительно напряже­ний  и . Растягивающие нормальные напряжения, т. е. совпа­дающие с направлением внешней нормали, будем считать положи­тельными. Касательное напряжение будем считать положительным, если при повороте вектора  против хода часовой стрелки на 90° его направление совпадает с направлением внешней нормали. Не­трудно видеть, что в рассмотренном нами случае напряжения  и  являются положительными.

Из формул (2.12) и (2.13) следует, что в элементарных пло­щадках, лежащих на некотором наклонном сечении, возника­ют как нормальные, так и касательные напряжения. Исследуем их изменение в зависимости от угла α. При α = 0°  = σ = σ_max, т. е. в поперечных сечениях, возникают максимальные нормаль­ные напряжения. При α = 90° (по площадкам, параллельным оси стержня)  = 0 и  = 0, т. е. продольные слои растянутого (или сжатого) стержня не имеют друг с другом силового взаи­модействия по боковым поверхностям. Поэтому растяжение стержня можно уподобить растяжению пучка не связанных меж­ду собой параллельных нитей. При α = 45° т. е.  максимальные касательные напряжения действуют по сечени­ям, наклоненным под углом 45° к оси стержня, причем величи­на максимального касательного напряжения равна половине нормального, возникающего в поперечных сечениях.

                           

 

 

Рис. 2.8.

Установим в заключение связь между касательными напря­жениями, возникающими на двух взаимно перпендикулярных площадках. Для этой цели рассмотрим две такие площадки, оп­ределяемые соответственно углами α и β, причем β = α + 90° (см. рис. 2.8). Для площадки, наклоненной под углом α по фор­муле (2.12) имеем 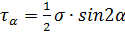. Для площадки, наклоненной под углом β = α + 90°, по той же формуле имеем

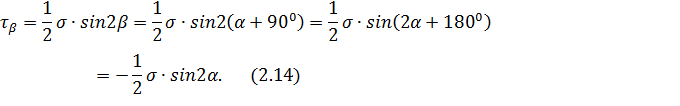
Сопоставляя выражения для  и , можем сделать следую­щий важный вывод:

т. е. касательные напряжения по двум взаимно перпендикулярным площадкам равны по величине и противоположны по зна­ку. Это положение является частным случаем закона парности касательных напряжений.

Рассмотрим теперь более общий слу­чай плоского (двухосного) напряженно­го состояния, когда отличны от нуля два главных напряжения σ₁, и σ₂ (рис. 2.9).

Положительный угол α между на­правлением σ₁, и нормалью к произвольной площадке будем по-прежнему отсчитывать против хода часовой стрел­ки. Между направлением напряжения σ₂ и площадкой угол равен (α + 90°).

Напряжения  и  в произвольном наклонном сечении вычисляют по фор­мулам (2.12), (2.13), суммируя напряже­ния от действия σ₁ с напряжением от действия σ₂ (при замене угла α на угол (α + 90°)). В результате получим

 

Рис. 2.9

  Легко убедиться в том, что напряжения  и  в наклонном сечении, перпендикулярном рассмотренному, могут быть подсчи­таны по формулам

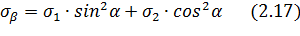
Сравнивая (2.14) и (2.18), мы видим, что закон парности касатель­ных напряжений сохраняет свою силу и для двухосного напря­женного состояния.

Рассмотрим важные частные случаи.

1-й случай, σ₁ = σ₂ = σ (рис. 2.10, а).

Рис. 2.10

Из формул (2.14) следует, что на всех площадках, проходящих через исследуемую точку, касательное напряжение  равно нулю, а нормальное напряжение имеет одно и то же значение . Такое напряженное состояние называется равномерным двухос­ным растяжением.

2-й случай. Напряженное состояние (рис. 2.10, б) характери­зуется главными напряжениями σ₁ = σ и σ₃ = —σ.

Здесь σ₂ = 0. Определяя по формулам (2.14) напряжения в сечениях, одинаково наклоненных к направлениям σ₁ и σ₃, полу­чим  = 0, a  = ±σ. Такое напряженное состояние называется чистым сдвигом.

Приведем без вывода результаты решения обратной задачи, когда требуется по значениям заданных нормальных ,  и касатель­ных ,  напряжений, действующих по граням элемента, опреде­лить значения главных напряжений и положение основных площадок. Формулы для определения главных напряжений σ_max, σ_mjn и угла наклона основных площадок α₀ имеют следующий вид:

                                                                                          

 

Обобщенный закон Гука

Определим деформации ε₁, ε₂ и ε₃ в направлениях главных на­пряжений для трехосного напряженного состояния. Для этого используем закон Гука для одноосного напряженного состоя­ния, зависимость между продольной и поперечной деформация­ми и принцип независимости действия сил (принцип сложения деформаций).

Относительное удлинение в направлении главного напряже­ния σ₁ складывается из составляющей σ₁/E, обусловленной дей­ствием главного напряжения σ₁, и составляющих 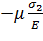, , обусловленных действием главных напряжений σ₂ и σ₃. Следовательно,

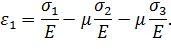
Такие же выражения получаются для ε₂ и ε₃. В итоге имеем:

Уравнения (2.18) представляют собой обобщенный закон Гука для объемного напряженного состояния. Деформации ε₁, ε₂ и ε₃ в направлениях главных напряжений называются главными де­формациями. Для плоского напряженного состояния (σ₃ = 0) оп­ределение главных напряжений σ₁, и σ₂ по известным главным деформациям ε₁ и ε₂ производится по формулам

                                                                     (2.21)

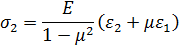
С учетомε₁, ε₂ и ε₃ можно вычислить изменение объема при деформации кубика размером 1x1x1 и объемом V ₀ = 1. После деформации его объем

(произведениями ε как величинами малыми по сравнению с са­мими ε пренебрегаем).

Относительное изменение объема, как объемная деформация,

Подставив значения ε₁, ε₂ и ε₃ из уравнений (2.7), получим

Из формулы (2.22) следует, что коэффициент Пуассона μ не может быть больше 0,5, поскольку при трехосном растяжении, очевидно, объем элемента не способен уменьшиться. При μ = 0,5 ε_V= 0, т. е. объем элемента при деформации не изменяется.

Лекция №3

3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ. СТАТИЧЕСКИЕ МОМЕНТЫ, МОМЕНТЫ ИНЕРЦИИ И МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЙ. ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ (ТЕОРЕМА ГЮЙГЕНСА).

Рис. 3.1

  Известно, что сила, которую может выдержать стержень на растяжение, пропорциональна площади поперечного сечения. Однако, площадь поперечного сечения не является исчерпывающей характеристикой. Сечения разной конфигурации могут иметь одинаковую площадь, но их поведение при различных способах нагружения будет различным. Простейший пример: полоса металла или бумаги, будучи согнутой (угловое сечение) приобретает способность сопротивляться изгибу в гораздо большей мере, чем такая же плоская полоса.

Для того, чтобы охарактеризовать геометрические свойства поперечных сечений стержней при различных способах нагружения, необходимо ввести более сложные характеристики – моменты площадей.

Предыдущая12345678910111213Следующая

Поделиться:

Воспользуйтесь поиском по сайту: