 |
Формула Эйлера для определения критической силы
|
|
|
|
Рассматриваем стержень с шарнирно закрепленными концами (рис. 7.4).
| Рис. 7.4. |

| Рис. 7.5 |
 Предположим, что он сжимается силой
Предположим, что он сжимается силой  , равной критической. По Эйлеру при этом возможны две формы равновесия: прямая и изогнутая. Потеря устойчивости всегда происходит в плоскости наименьшей жесткости (рис. 7.5), поэтому в расчет входит минимальные момент инерции сечения. Пусть известны:
, равной критической. По Эйлеру при этом возможны две формы равновесия: прямая и изогнутая. Потеря устойчивости всегда происходит в плоскости наименьшей жесткости (рис. 7.5), поэтому в расчет входит минимальные момент инерции сечения. Пусть известны:  -длина стержня,
-длина стержня,  -модуль упругости материала,
-модуль упругости материала,  -минимальный момент инерции.
-минимальный момент инерции.
Выбираем систему координат  . В этой системе координаты произвольного сечения изогнутой оси будут
. В этой системе координаты произвольного сечения изогнутой оси будут  .
.
Требуется вывести формулу для определения величины критической сипы. Записываем приближенное дифференциальное уравнение изогнутой оси, вычисляя момент относительно сечения в деформированном состоянии бруса 

Знак выбираем так, чтобы в обоих частях равенства были одинаковые знаки
 ;
;  ;
; 
Преобразовываем и решаем уравнение:
 ;
; 

характеристическое уравнение
 ;
; 
общее решение
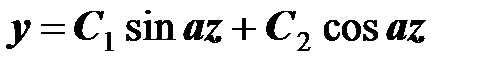
Для определения  и
и  - используем условия закрепления
- используем условия закрепления
1) 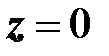 ,
, 
2)  ,
, 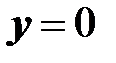 .
.
Из первого: 


 ,
,
изогнутая ось имеет форму синусоиды.
Из второго
 ,
,
возможны два случая:
1)  ,
,  ,
,
что дает 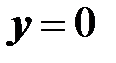 , что соответствует не изогнутой оси, тривиальное решение.
, что соответствует не изогнутой оси, тривиальное решение.
2))  ,
, 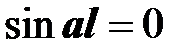 ,
,
 ;
;
откуда получим
 ;
;  ;
; 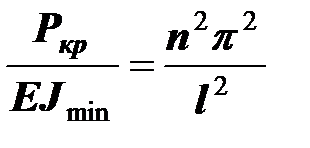
 ,
, 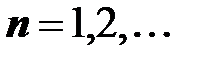

| Рис.7.6 14.6. |
Рассмотрим, какой смысл имеет 
 .
.
Видим, что  - число полуволн, которые образуются при потере устойчивости. Следовательно, каждой критической силе соответствует свое число полуволн (рис. 7.6).
- число полуволн, которые образуются при потере устойчивости. Следовательно, каждой критической силе соответствует свое число полуволн (рис. 7.6).
При статическом нагружении сила растет постепенно, как только станет  произойдет потеря устойчивости с одной полуволной.
произойдет потеря устойчивости с одной полуволной.
|
|
|
При ударном нагружении можно сразу создать большую силу, например, взрывом. При этом можно получить потерю устойчивости с большим числом полуволн. (Пример с забиванием гвоздя).
Из граничных условий мы определили  и
и  , постоянная
, постоянная  осталась неопределённой. Это следствие того, что использовалось приближенное уравнение. Мы смогли определить величину критической силы, но величина прогиба осталась неопределенной. Если использовать точное уравнение, прогиб можно определить. В большинстве практических задач достаточно найти
осталась неопределённой. Это следствие того, что использовалось приближенное уравнение. Мы смогли определить величину критической силы, но величина прогиба осталась неопределенной. Если использовать точное уравнение, прогиб можно определить. В большинстве практических задач достаточно найти  , так как при
, так как при  происходит разрушение и величина прогиба никого уже не интересует.
происходит разрушение и величина прогиба никого уже не интересует.
Зависимость критической силы от способа закрепления концов стержня
Общая формула для критической силы имеет вид:

Преобразуем формулу, введя величину  , обратную числу полуволн
, обратную числу полуволн
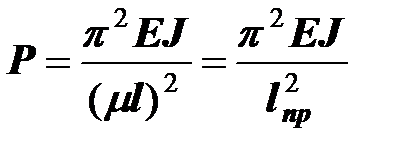 ,
,
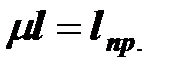 - приведенная длина, равная длине одной полуволны при потере устойчивости,
- приведенная длина, равная длине одной полуволны при потере устойчивости,
 - коэффициент длины.
- коэффициент длины.
| Рисунок 7.7. |

Формулу Эйлера будем использовать в виде:
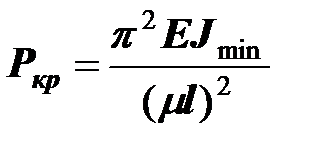 ,
,
где  -коэффициент, зависящий от способа закрепления концов.
-коэффициент, зависящий от способа закрепления концов.
Понятие о потере устойчивости за пределом пропорциональности.
Гибкость.
1. При расчетах на устойчивость основной геометрической характеристикой стержня является гибкость.
Проведем ряд преобразований в формуле для определения критического напряжения по Эйлеру:
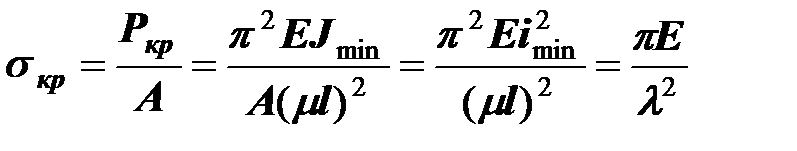 ,
, 

Гибкостью стержня называют величину

Это геометрическая величина, зависящая от размеров сечения стержня, его длины и способа закрепления концов.
2. Рассмотрим, всегда ли применима формула Эйлера. Для этого вспомним, при каких предположениях она выводится. Используется приближенное дифференциальное уравнение упругой линии
 ,
,
следовательно, формула Эйлера справедлива только при малых деформациях и при напряжениях, не превышающих предел пропорциональности, так как за пределом пропорциональности модуль  теряет смысл, напишем условие применимости Формулы Эйлера.
теряет смысл, напишем условие применимости Формулы Эйлера.
|
|
|
 ;
;  ;
;  ;
;
Обозначим
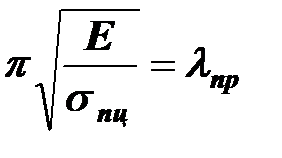
 - предельная гибкость. В отличие от просто гибкости эта величина не геометрическая, а физическая, так как зависит от материала стержня.
- предельная гибкость. В отличие от просто гибкости эта величина не геометрическая, а физическая, так как зависит от материала стержня.
Если  формула Эйлера применима,
формула Эйлера применима,
если  , то не применима.
, то не применима.
3. Определение критического напряжения за пределом упругости. Все стержни, работающие на сжатие, можно разделить на три группы: большой, средней и малой гибкости.
Стержнями большой гибкости считаются стержни, для которых  , они рассчитываются по формуле Эйлера.
, они рассчитываются по формуле Эйлера.
Стержнями малой гибкости считаются стержни, для которых  , то есть потеря прочности происходит раньше потери устойчивости. Эти стержни на устойчивость не рассчитываются, для них принимают
, то есть потеря прочности происходит раньше потери устойчивости. Эти стержни на устойчивость не рассчитываются, для них принимают 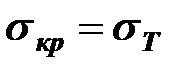 .
.
Стержнями средней гибкости считаются стержни, для которых  . К ним формула Эйлера не применима, но устойчивость теряется раньше, чем прочность. Существует несколько теорий для определения критических напряжений стержней средней гибкости.
. К ним формула Эйлера не применима, но устойчивость теряется раньше, чем прочность. Существует несколько теорий для определения критических напряжений стержней средней гибкости.
Наибольшее распространение в России получила теория Ясинского:

где  и
и  - постоянные, зависящие от материала.
- постоянные, зависящие от материала.

| Рисунок 7.8. |
 , то есть постоянное, для стержней большой гибкости на графике получается гиперболическая зависимость (гипербола Эйлера), для стержней средней гибкости формула Ясинского дает прямую линию. Следует отметить, что формула Ясинского не вполне согласуется с опытом, экспериментальные точки располагаются несколько выше прямой, но эта погрешность идет в запас прочности (устойчивости). Существуют другие формулы (Кармана, Энгессера, Шенли), по которым вычисленные напряжения лучше согласуются с опытом, но они неудобны для расчетов, так как в них входит переменный модуль
, то есть постоянное, для стержней большой гибкости на графике получается гиперболическая зависимость (гипербола Эйлера), для стержней средней гибкости формула Ясинского дает прямую линию. Следует отметить, что формула Ясинского не вполне согласуется с опытом, экспериментальные точки располагаются несколько выше прямой, но эта погрешность идет в запас прочности (устойчивости). Существуют другие формулы (Кармана, Энгессера, Шенли), по которым вычисленные напряжения лучше согласуются с опытом, но они неудобны для расчетов, так как в них входит переменный модуль 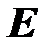 , для вычисления которого надо знать напряжения.
, для вычисления которого надо знать напряжения.
| Рис.7.9. 7.9.14.9. |
 7.5. Расчет на устойчивость по коэффициенту снижения допускаемого напряжения
7.5. Расчет на устойчивость по коэффициенту снижения допускаемого напряжения
При использовании формул Эйлера и Ясинского надо все время проверять, какая из них применима. На практике это неудобно. Используется другой способ: расчет на устойчивость заменяется расчетом на простое сжатие с меньшим допускаемым напряжением.
|
|
|
Запишем допускаемые напряжения при простом сжатии и с учетом потери устойчивости:
 ;
; 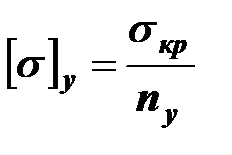 .
.
Поделим одно выражение на другое
 ;
;  .
.
Полученный коэффициент 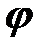 называется коэффициентом снижения основного допускаемого напряжения. Он зависит от материала
называется коэффициентом снижения основного допускаемого напряжения. Он зависит от материала 
 , принятого запаса
, принятого запаса  и гибкости
и гибкости  . Значения коэффициента приводятся в таблицах. Чтобы в таблице найти
. Значения коэффициента приводятся в таблицах. Чтобы в таблице найти 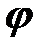 ,нужно знать материал и гибкость стержня.
,нужно знать материал и гибкость стержня.
Основная расчетная формула
 ;
; 
Существует два основных типа задач расчета на устойчивость.
1. Определение допускаемой силы  . При этом задается материал стержня, его геометрические размеры и способ закрепления. По формуле
. При этом задается материал стержня, его геометрические размеры и способ закрепления. По формуле  вычисляется допускаемая сила.
вычисляется допускаемая сила.
Пример: Двутавровая стойка №30а, длиной 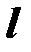 =2м жестко защемлена одним концом, а на другом сжимается силой
=2м жестко защемлена одним концом, а на другом сжимается силой 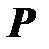 (рис. 14.9). Определить допустимую величину силы. По таблице находим:
(рис. 14.9). Определить допустимую величину силы. По таблице находим:
 = 160 МПа = 160 •106 Н/м2
= 160 МПа = 160 •106 Н/м2
 = 61,2 см2 = 61,2*10-4 м2
= 61,2 см2 = 61,2*10-4 м2
 =
=  = 2,55 см = 2,55*10-2 м.
= 2,55 см = 2,55*10-2 м.
Вычисляем гибкость

По таблице находим 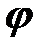 проводя интерполяцию
проводя интерполяцию
 ;
;  ;
; 
Определяем допустимую силу:
 =0,299*160*106*61*10-4=293 кН.
=0,299*160*106*61*10-4=293 кН.
2. Подбор сечения. Задается сжимающая сила, материал стойки, её длина, способ закрепления и формы сечения. Требуется определить размеры сечения.
Пример: Стальная стойка квадратного сечения, длиной  =2 м, шарнирно закреплена по концам и сжимается силой
=2 м, шарнирно закреплена по концам и сжимается силой  = 80 кН (рис. 7.10). Требуется определить необходимые размеры сечения
= 80 кН (рис. 7.10). Требуется определить необходимые размеры сечения 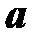 .
.
Для стали  = 160*106 Н/м2.
= 160*106 Н/м2.

| Рис.7.10. |

содержит две неизвестных 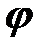 и
и  , которые между собой связаны. Из одного уравнения найти две неизвестных нельзя. Поэтому задача решается подбором с последовательными приближениями.
, которые между собой связаны. Из одного уравнения найти две неизвестных нельзя. Поэтому задача решается подбором с последовательными приближениями.
Предварительно выразим геометрические характеристики и гибкость  через
через  ,
,
 ;
;  ;
; 

Задаем произвольно  =0,6
=0,6
Вычисляем


Проверяем, хорошо ли подобрали сечение:
 ,
,  =0
=0
Полученное фактическое значение  сильно отличается от
сильно отличается от  предполагаемого. Пробуем ещё раз,
предполагаемого. Пробуем ещё раз,
Задаем
 =0,3;
=0,3;  =16,6*10-4;
=16,6*10-4;  =7,1*10-2;
=7,1*10-2;  =168;
=168;  =0,27
=0,27
Теперь  и
и  отличаются на 0,03.Вычислим допускаемую силу
отличаются на 0,03.Вычислим допускаемую силу
 =0,3*160*106*16,6*10-4=79,7 кН
=0,3*160*106*16,6*10-4=79,7 кН
|
|
|
Она отличается от заданной на
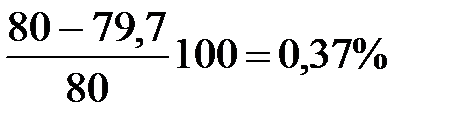
Это расхождение допустимо. Принимаем сечение: квадрат со стороной а =0,041 м = 4,1см.
|
|
|


