 |
Центробежный момент инерции
|
|
|
|
Если в уравнении 3.1 т= 1, п= 1, получим характеристику центробежного момента инерции
Если хотя бы одна из осей x или y является осью симметрии сечения, центробежный момент инерции такого сечения относительно этих осей равен нулю (так как в этом случае каждой положительной величине 
, можем поставить в соответствие точно такую же, но отрицательную, по другую сторону от оси симметрии сечения, см. рис.3.2).
| Рис. 3.3 |
Полярный момент инерции
Полярным моментом инерции 
называют сумму произведений элементарных площадей dA на квадраты их расстояний до выбранной точки взятых по всей площади сечения А., но 
С другой стороны,
Размерность моментов инерции в СИ – м4. Полярный момент инерции равен сумме осевых.
Обратим внимание на очевидный факт:
1. осевые моменты инерции 
и полярный момент инерции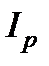 
всегда положительны, а статические моменты и центробежный момент инерции могут принимать как положительные, так и отрицательные значения.
2. Момент (любой из моментов) составной площади равен сумме моментов ее частей.
3. Если фигура ограничена двумя замкнутыми контурами, то ее момент можно вычислить, вычитая из момента площади, ограниченной внешним контуром, момент площади ограниченной внутренним контуром.
4. Если хотя бы одна из осей является осью симметрии, то центробежный момент инерции относительно данных осей равняется нулю.
Это очевидно, т.к. фигуру можно представить, как множество пар элементарных площадок, имеющих равными одну из координат и равными по величине и противоположными по знаку другую.
|
|
|
3.2.1. Преобразование моментов инерции при параллельном переносе осей.
Пусть x, y - центральные оси для данной фигуры, а x 1 и y1 - произвольные оси параллельные осям x и y.
Найдем моменты инерции для осей 
и 
, через, как выражаются, “старые” моменты инерции относительно осей 
и 
.
Связь между “новыми” и “старыми” координатами произвольной элементарной площадки будут выглядеть
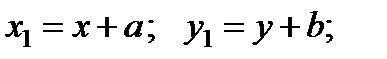
где 
и 
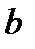- координаты старого центра в новых осях. Подставляя эти выражения в формулы для моментов инерции, и учитывая, что оси x, y - центральные получаем:
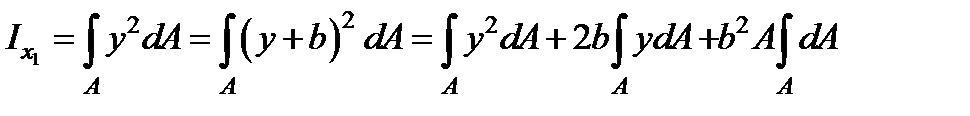
Проделывая аналогичные выкладки и для других моментов, получаем следующий закон преобразования моментов инерции:
; 
; 
(3.13)
Первыми двум выражениям можно придать словесную формулировку: момент инерции относительно какой-либо оси равняется моменту относительно оси центральной параллельной данной плюс площадь на квадрат расстояния между осями.
3.2.2. Преобразование моментов инерции при повороте осей.
Пусть х, у произвольной площади сечения площадью А, а оси x 1, y 1 получены из них поворотом на угол α. Найдем моменты инерции относительно осей x 1, y 1 через “старые” моменты инерции относительно осей х, у.
Связь между координатами известна из курса аналитической геометрии
Вычислим момент инерции 
Входящие в это выражение, интегралы представляют собой моменты инерции относительно осей x, y.
(3.14)
Учитывая известные тригонометрические тождества:
(3.15)
переходим к функциям угла 2α.
Если проделать эту процедуру и для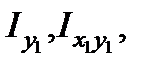 
то получим следующие формулы преобразования моментов инерции при повороте координатных осей:
(3.16)
Складываем два первых уравнения, получаем
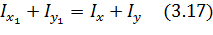
т.е. сумма осевых моментов инерции инвариантна по отношению к повороту осей (на самом деле, она ведь равна полярному моменту инерции, а последний зависит лишь от полюса, а не от положения осей x, y). 
|
|
|
|
|
|
