Некоторые сведения о геометрических характеристиках

Геометрические характеристики - числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как след­ствие, характеризующие сопротивление элемента различным видам дефор­мации).

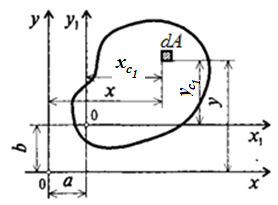
Рассмотрим произвольное поперечное сечение А (сечение бруса) (рис. 3.1) с координатами центра тяжести x _c, у _c. В точке (x,у) выделим элемент площади dA. Основные геометрические характеристики попе­речных сечений элементов конструкций описываются интегра­лами следующего вида

Рассмотрим некоторые характерные варианты записи этого интеграла и получим выраже­ния для основных геометрических характеристик.

Площадь поперечного сечения

При т=0, n =0 интеграл приобретает вид

 

а соответствующая характеристика, как видим, представляет собой площадь поперечного сечения элемента.

Как было указано во многих случаях деформирования тела знание только площади его по­перечного сечения недостаточно.

3.1. Статические моменты

Статический момент относительно данной оси - сумма произведений эле­ментарных площадей dA на их расстояние до данной оси, взятая по всей площади сечения А.

Если в уравнении 3.1 т=1, n =0, тогда получим статическим моментом относительно оси x

при т=0, п=1, получим выражение для статическим моментомотносительно оси у.

Для сложного сечения (состоящего из нескольких простых, каждое из кото­рых имеет площадь А _i и координаты собственного центра тяжести )

 

Рис. 3.2

Отсюда можем получить формулы для определения координат центра тяже­сти сечения:                                                                      

Статические моменты в этом случае равны нулю, а сами оси называются центральными. Размерность статических моментов в системе СИ – м³.

При выполнении практических расчетов важно знать, как ме­няются статические моменты сечения при параллельном переносе координатных осей (рис 3.1).

В соответствии с рисунком 3.1, очевидно, что

х = х₁ + а у = у₁ + b. (3.3)

Подставляя (3.1) и (3.2) в (3.3) получим:

              

                                                                                   (3.4)                         

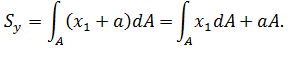
Величины a и b в уравнении 3.4 можно подобрать так, чтобы выполнялись следующие равенства (причем единственным обра­зом):

b∙A=S_x, a∙A=S_y, (3.5)

В этом случае статические моменты относительно осей будут равны = 0.

Точка С(х_с, y_c) пересечения централь­ных осей называется центром тяжести сечения в системе координат (х, у) и определяется из (3.5):

Если предположить, что брус имеет составное сечение с общей площадью A. Обозначим через A_k (k = 1,2,3,...,n) площадь k -ой области, принадлежащей к составному сечению бруса. Тогда выражение (3.1, 3.2) можно преобразовать в следующем виде:

 

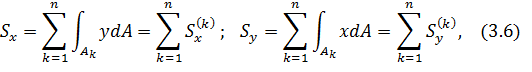
где - статические моменты k-той области относительно осей х и у., следовательно, статический момент составного сечения равен сумме статических моментов составляющих областей.

 

3.2. Моменты инерции сечения

Для оценки напряженного состояния нагружаемых элементов применяют еще три момента второго порядка

Первые две величины называют осевыми моментами инерции относительно осей x и y, а  - центробежным моментом инерции.

Кроме осевого и центрального момента инерции используется еще один интеграл , который называется полярным моментом инерции. Очевидно, что 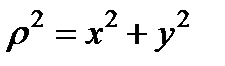, и:

,

Осевой момент инерции относительно данной оси — сумма произведений элементарныx площадей dA на квадрат их расстояний до данной оси, взятая по всей площади сечения А.

Если в уравнении 3.1 т = 2, n = 0, получаем, что осевым моментом инерции относительно оси x равен:

при т=0, n =2,                              

осевым моментом инерции относительно оси у.

Предыдущая12345678910111213Следующая

Поделиться:

Воспользуйтесь поиском по сайту: