 |
Влияние условий закрепления концов стержня на величину критической силы.
|
|
|
|
Формула (2) дает возможность определить критическую силу только в случае шарнирного опирания обоих концов стержня. Обобщим полученный результат на некоторые другие часто встречающиеся случаи закрепления.
а) Стержень, закрепленный жестко одним концом и свободный от закрепления на другом.
Очевидно, изгиб стержня в этом случае будет таким же, как и в случае шарнирно опертого стержня, но имеющего длину в 2 раза большую.
Критическая сила в этом случае будет равна критической силе шарнирно опертого стержня, имеющего длину
Введем понятие коэффициента приведения длины - 
, т.е. числа показывающего во сколько раз нужно увеличить длину шарнирно опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной 
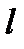при заданном закреплении. Очевидно, что в нашем случае 
.
Коэффициент 
можно трактовать как число, показывающее сколько раз длина стержня укладывается в длине полуволны синусоиды, по которой происходит потеря устойчивости.
Обобщим формулу Эйлера
Для некоторых других случаев закрепления коэффициент приведения длины равен:
Пределы применимости формулы Эйлера.
Формула Эйлера выведена в предположении, что материал линейно упруг, и, естественно, применима в тех случаях пока справедлив закон Гука.
Придадим формуле (3) иной вид.
Введем понятие критического напряжения, т.е. напряжения соответствующего критической силе
но 
где 
- минимальный радиус инерции сечения.
Введем еще одну величину – гибкость стержня 
тогда 
Тогда можно сказать, что формула Эйлера справедлива, если критические напряжения не превышают предела пропорциональности при сжатии: 
|
|
|
Выясним, при каких гибкостях можно использовать формулу Эйлера.
Приравняем в (4) 
Если 
то можно использовать формулу (3).
Для малоуглеродистых сталей, особенно часто используемых для сжатых элементов: 
тогда
т.е. для малоуглеродистых сталей формулу Эйлера можно использовать при гибкостях больших 100.
Зависимость критической силы от способа закрепления концов стержня
Общая формула для критической силы имеет вид:
Преобразуем формулу, введя величину 
, обратную числу полуволн
,
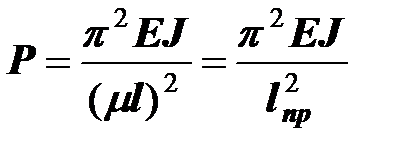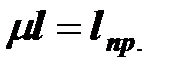- приведенная длина, равная длине одной полуволны при потере устойчивости,
- коэффициент длины.
Формулу Эйлера будем использовать в виде:
,
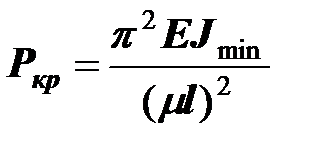где -коэффициент, зависящий от способа закрепления концов.
Понятие о потере устойчивости за пределом пропорциональности.
Гибкость.
1. При расчетах на устойчивость основной геометрической характеристикой стержня является гибкость.
Проведем ряд преобразований в формуле для определения критического напряжения по Эйлеру:
, 
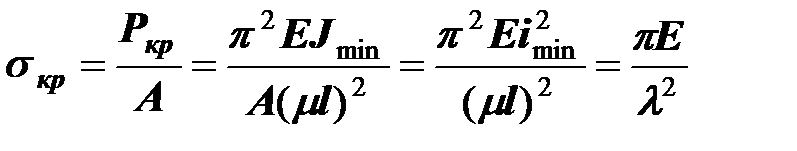Гибкостью стержня называют величину
Это геометрическая величина, зависящая от размеров сечения стержня, его длины и способа закрепления концов.
2. Рассмотрим, всегда ли применима формула Эйлера. Для этого вспомним, при каких предположениях она выводится. Используется приближенное дифференциальное уравнение упругой линии
,
следовательно, формула Эйлера справедлива только при малых деформациях и при напряжениях, не превышающих предел пропорциональности, так как за пределом пропорциональности модуль 
теряет смысл, напишем условие применимости Формулы Эйлера.
; 
; 
;
Обозначим
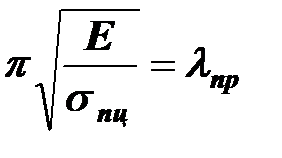
- предельная гибкость. В отличие от просто гибкости эта величина не геометрическая, а физическая, так как зависит от материала стержня.
Если 
формула Эйлера применима,
если 
, то не применима.
3. Определение критического напряжения за пределом упругости. Все стержни, работающие на сжатие, можно разделить на три группы: большой, средней и малой гибкости.
|
|
|
Стержнями большой гибкости считаются стержни, для которых 
, они рассчитываются по формуле Эйлера.
Стержнями малой гибкости считаются стержни, для которых 
, то есть потеря прочности происходит раньше потери устойчивости. Эти стержни на устойчивость не рассчитываются, для них принимают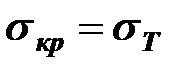 
.
Стержнями средней гибкости считаются стержни, для которых 
. К ним формула Эйлера не применима, но устойчивость теряется раньше, чем прочность. Существует несколько теорий для определения критических напряжений стержней средней гибкости.
Наибольшее распространение в России получила теория Ясинского:
где 
и 
- постоянные, зависящие от материала.
| Рисунок 7.8. |
, то есть постоянное, для стержней большой гибкости на графике получается гиперболическая зависимость (гипербола Эйлера), для стержней средней гибкости формула Ясинского дает прямую линию. Следует отметить, что формула Ясинского не вполне согласуется с опытом, экспериментальные точки располагаются несколько выше прямой, но эта погрешность идет в запас прочности (устойчивости). Существуют другие формулы (Кармана, Энгессера, Шенли), по которым вычисленные напряжения лучше согласуются с опытом, но они неудобны для расчетов, так как в них входит переменный модуль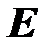 
, для вычисления которого надо знать напряжения.
| Рис.7.9. 7.9.14.9. |
Расчет на устойчивость по коэффициенту снижения допускаемого напряжения
При использовании формул Эйлера и Ясинского надо все время проверять, какая из них применима. На практике это неудобно. Используется другой способ: расчет на устойчивость заменяется расчетом на простое сжатие с меньшим допускаемым напряжением.
Запишем допускаемые напряжения при простом сжатии и с учетом потери устойчивости:
; 
.
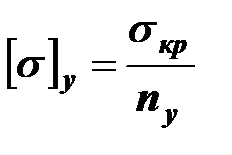Поделим одно выражение на другое
; 
.
Полученный коэффициент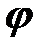 
называется коэффициентом снижения основного допускаемого напряжения. Он зависит от материала 
, принятого запаса 
и гибкости 
. Значения коэффициента приводятся в таблицах. Чтобы в таблице найти 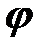,нужно знать материал и гибкость стержня.
|
|
|
Основная расчетная формула
; 
Существует два основных типа задач расчета на устойчивость.
Приведенное выше решение пригодно только для сравнительно длинных и тонких стержней. В случае более коротких и жестких стержней потеря устойчивости происходит при возникновении пластических деформаций, и задача требует специального рассмотрения. Существуют решения (Т.Карман, Энгессер) об устойчивости стержня за пределами упругости. Иногда прибегают к эмпирическим формулам типа формулы Ясинского 
где
и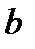 
- константы, зависящие от свойств материала.
|
|
|
