 |
Сдвиг. Кручение. Расчёт на сдвиг (срез). Крутящий момент. Деформации и напряжения. Расчёт на прочность и жёсткость при кручении.
|
|
|
|
4.1. Определение внутренних усилий при сдвиге
Кроме деформации растяжения или сжатия материал нагруженного элемента конструкции может испытывать деформацию сдвига.
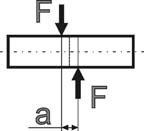Сдвиг – вид сопротивления, при котором стержень нагружен двумя равными силами (на малом расстоянии друг от друга), перпендикулярными к оси бруса и направленными в противоположные стороны.
Примером такого действия сил на брус может быть разрезание ножницами прутьев, деформация заклепок, болтов, сварных швов между металлическими листами и т. п. Вообще же на практике сдвиг в чистом виде получить трудно, так как обычно деформация сдвига сопровождается другими видами деформаций и чаще всего изгибом.
Установим формулы для внутренних усилий, напряжений и деформаций, необходимые при расчете на сдвиг элементов конструкций, имеющих форму бруса. Пусть известна внешняя нагрузка F, вызывающая сдвиг одной части бруса относительно другой. Используя метод мысленных сечений (см. рисунок), находим величину внутренних усилий, действующих в сечении бруса. Очевидно, что в данном случае нагружения из шести уравнений равновесия лишь одно не обращается тождественно в ноль:
∑ Fy =0⇒ Q y = F.
Таким образом, при сдвиге из шести внутренних усилий (N, Qy, Qz, Mx, My, Mz) в сечении элемента конструкции возникают только одно – поперечная сила (Qy или Q x).
4.2. Определение напряжений при сдвиге.
Так как поперечная сила Qy (или Q x) является единственным внутренним усилием, возникающим в сечении стержня при сдвиге, и при этом она лежит в плоскости этого сечения, то и напряжения, возникающие здесь, должны лежать в плоскости сечения стержня. То есть при сдвиге в точках поперечного сечения стержня возникают только касательные напряжения τ.
|
|
|
В соответствии с определением, касательные напряжения τ, действующие в поперечном сечении (A) бруса, представляют собой интенсивность внутренних поперечных сил
исходя из чего можем записать (опуская соответствующие индексы):
При сдвиге условно считают, что касательные напряжения равномерно распределены по площади поперечного сечения (τ= const), поэтому Q = τ⋅ A.
Тогда касательные напряжения при сдвиге определяются так:
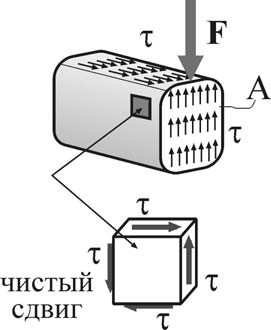
Рассмотрим характер напряженно-деформированного состояния, которое возникает в точках стержня при сдвиге.
По закону парности касательных напряжений в продольных сечениях бруса, так же как и в его поперечных сечениях будут возникать только касательные напряжения. Тогда на гранях (параллельных соответствующим осям координат) бесконечно малого элемента, «вырезанного» в окрестности любой точки стержня при сдвиге, будут действовать только касательные напряжения τ. Такой случай напряженного состояния называют чистым сдвигом.
Чистый сдвиг – частный случай плоского напряженного состояния, при котором по граням прямоугольного элемента действуют только касательные напряжения.
Определим величину и направление главных напряжений при чистом сдвиге:
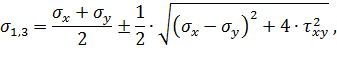
так как σ x =σ y =0, то можем записать σ1 =τx y, σ3 =−τ x y.
Направление главных площадок определяется углом α, который найдем по формуле
учитывая, что σ x =σ y =0,
Как видим, при чистом сдвиге главные напряжения одинаковы по величине, противоположны по знаку (σ1= –σ3= τ xy) и направлены под углом 45о к оси стержня (третья главная площадка элемента совпадает с ненагруженной фасадной гранью элемента, следовательно, σ2=0).
4.3. Определение деформаций и закон Гука при чистом сдвиге
Рассмотрим деформацию квадратного элемента при чистом сдвиге (см. рисунок).
|
|
|
Поскольку по граням элемента не действуют нормальные напряжения, то вдоль граней нет и удлинений. В то же время диагональ, совпадающая с направлением σ1, удлинится, а другая диагональ, совпадающая с направлением сжимающего напряжения σ3, укоротится. В результате квадрат трансформируется в ромб без изменения длины граней. Таким образом, деформация чистого сдвига характеризуется изменением первоначально прямых углов.
Более наглядное представление о деформации элемента при сдвиге можно получить, закрепив одну из граней (см. рисунок).
Малый угол γ xy, на который изменяется первоначально прямой угол элемента при сдвиге, называется углом сдвига или относительным сдвигом:
Величину абсолютного смещения грани обозначают ∆ s и называют абсолютным сдвигом.
Из треугольника BAB 1 следует, что
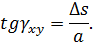
Учитывая малость угла, можно считать, что
tgγ ≈γ xy,
тогда окончательно запишем взаимосвязь между относительным и абсолютным сдвигом элемента
Зависимость между нагрузкой и деформацией при сдвиге можно проследить по так называемой диаграмме сдвига, которую получают обычно из опытов на кручение тонкостенных трубчатых образцов (в стенках которых, как увидим далее, также возникает напряженное состояние чистого сдвига). Для пластичных материалов диаграмма сдвига аналогична диаграмме растяжения и имеет с ней одинаковые характерные участки, в том числе и участок упругости.
Рассматривая деформацию сдвига в пределах упругости, найдем, что между углом сдвига γ xy и касательными напряжениями τ xy существует линейная зависимость, которая носит название закона Гука при сдвиге и может быть выражена следующими формулами:
τ xy = G ⋅γ xy, (4.3)
где G – коэффициент пропорциональности, который называется модулем упругости при сдвиге или модулем упругости второго рода и является константой для данного материала. Модуль сдвига может быть определен аналитически, если известны величины модуля Юнга и коэффициента Пуассона:
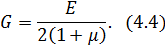
Заметим, что все рассмотренные характеристики упругости материала E, µ, G, K взаимосвязаны, однако в сопротивлении материалов и в теории упругости только две из них (чаще всего E и µ) принимаются независимыми.
|
|
|
Подставляя выражения (4.1) и (4.2) в формулы (4.3), можно записать закон Гука при сдвиге и во «внешних формах» (через абсолютные деформации и внутренние усилия):
где a – расстояние между сдвигаемыми гранями; A – площадь грани.
4.4. Расчет на прочность и допускаемые напряжения при сдвиге
Проверим прочность элемента, испытывающего деформацию чистого сдвига. Пусть касательные напряжения на гранях элемента максимальны и равны τ max, а допускаемое напряжение для материала при растяжении – [σ].
Если для материала известна величина допускаемых касательных напряжений при сдвиге [τ], то условие прочности может быть записано в виде:
Величина допускаемых напряжений [τ] зависит от свойств материала, характера нагрузки, типа элементов конструкции и для чистого сдвига определяется обычно по III теории прочности:
σэквIII ≤ [σ].
Учитывая, что по III теории прочности
σэквIII = σ1 −σ3,
а при чистом сдвиге
σ1 =−σ3 = τ max,
можем записать
τ max = − (-τ max)≤ [σ],
или
Сравнивая выражения (4.6) и (4.7), заметим, что по III теории прочности
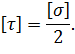
Полученную величину допускаемых касательных напряжений [τ] используют при расчетах на прочность деталей, испытывающих деформацию сдвига, в соответствии с условием прочности (4.6).
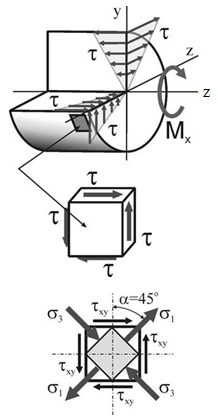
4.5. Определение внутренних усилий при кручении
Кручение – простой вид сопротивления (нагружения), при котором на стержень действуют моменты в плоскостях, перпендикулярных к продольной оси стержня.
Стержень, работающий на кручение, в дальнейшем будем называть валом.
Используя метод мысленных сечений (см. рисунок), находим величину внутренних усилий, действующих в сечении вала при кручении. Очевидно, что в данном случае нагружения из шести уравнений равновесия, составленных для отсеченной части стержня относительно внешних сил и внутренних усилий, лишь одно не обращается тождественно в ноль:
∑ Mx =0⇒ M M z = M кр .
Таким образом, при кручении в произвольном поперечном сечении вала из шести внутренних силовых факторов возникает только один – внутренний крутящий момент (М z).
|
|
|
4.6. Определение напряжений и деформаций при кручении
Выведем формулу для определения касательных напряжений τ и найдем зависимость между углом закручивания ϕ и внутренним крутящим моментом Мx. Данная задача применительно к валам круглого сечения может быть решена с помощью элементарного математического аппарата, если ввести соответствующие гипотезы, которые достаточно хорошо подтверждаются экспериментами.
Гипотезы, принимаемые при расчете на кручение:
1) сечения, плоские до деформации, остаются плоскими и после деформации (гипотеза Бернулли, гипотеза плоских сечений);
2) все радиусы данного сечения остаются прямыми (не искривляются) и поворачиваются на один и тот же угол ϕ, то есть каждое сечение поворачивается относительно оси x как жесткий тонкий диск;
3) расстояния между сечениями при деформации не изменяются.
4.7. Статическая сторона задачи
Чтобы определить напряжения в поперечных сечениях стержня, рассмотрим, прежде всего, статическую сторону задачи.
Поскольку крутящий момент М z – единственный внутренний силовой фактор в поперечном сечении, действующий при этом в плоскости данного сечения, можно предположить, что при кручении в поперечных сечениях вала возникают только касательные напряжения.
В сечении вала выделим элементарную площадку dA на расстоянии ρ от продольной оси (ось x) стержня. При кручении на площадке dA, будут действовать касательные напряжения τ, которые создадут элементарный крутящий момент dM z относительно оси x:
dM z = τ⋅ dA ⋅ρ.
Тогда полный момент, возникающий во всем сечении, найдем как
где τ – касательное напряжение, действующее на элементарной площадке dA, расположенной на произвольном расстоянии (радиусе) ρ от центра сечения.
Перпендикулярность вектора касательных напряжений радиусу объясняется отсутствием на поверхности вала касательных напряжений, параллельных его оси, и, соответственно (по закону парности касательных напряжений), отсутствием касательных напряжений вдоль радиуса.
Как видим, задача является внутренне статически неопределимой, так как неизвестен характер распределения касательных напряжений по сечению – τ(ρ)=?. В соответствии с общим планом решения статически неопределимых задач, рассмотрим геометрическую картину деформаций.
4.8. Геометрическая сторона задачи
Рассмотрим деформацию элемента стержня (вала) длиной dx, выделенного из закручиваемого стержня в произвольной точке с координатой x.
Условно примем, что левое сечение элемента d z остается неподвижным, а правое поворачивается на угол d ϕ, создаваемый за счет закручивания вала на длине d z. Один из радиусов OB, оставаясь прямым, поворачивается вместе с сечением на угол d ϕ, при этом точка B переходит в положение B 1, а образующая CB – в положение CB 1, поворачиваясь на угол γ – угол сдвига в этой точке вала.
|
|
|
Длину дуги BB 1 найдем из рассмотрения треугольников OBB 1 и CBB 1:
∪ BB 1 = ρ⋅ dφ = γ⋅ d z ⇒
4.9. Физическая сторона задачи
Запишем закон Гука, связывающий касательные напряжения с углом сдвига
τ = G ⋅γ. (4.10)
Математическая сторона задачи
Подставим выражение (4.9) в формулу (4.10):
а полученное выражение (4.11) – в формулу (4.8):
Так как в выражении (5.5) величины G и d ϕ/ dx, в соответствии с принятыми гипотезами, остаются постоянными по данному сечению, то их можно вынести за знак интеграла:
Величина
называется полярным моментом инерции и является геометрической характеристикой данного сечения.
Таким образом, окончательно можем записать
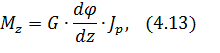
или, подставляя (4.11) в (4.13),
Откуда величина касательных напряжений при кручении определяется как:
Как видим, касательные напряжения распределены по сечению вала по линейному закону и достигают максимальной величины на поверхности вала (при ρ=ρ max):
где W ρ= J ρ/ρ max – полярный момент сопротивления.
Из формулы (5.7) легко найти и другие величины, характеризующие деформацию вала при кручении.
Величина 
называется относительным (погонным) углом закручивания и имеет размерность рад/м.
Используя выражение (4.15), найдем формулу для определения относительного угла закручивания:
Зная формулы (4.15) и (4.16) для определения относительного угла закручивания, можно записать формулу для определения взаимного угла поворота двух сечений, расположенных на расстоянии l друг от друга:
Если в пределах участка длиной l крутящий момент и геометрические характеристики сечения вала остаются постоянными, то угол закручивания можно определить, как
|
|
|
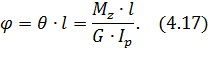
