|
2.3. Задачи для контрольных работ
|
|
|
|
2. 3. Задачи для контрольных работ
ЗАДАЧА 1
Стальной ступенчатый брус (Е = 2·105 МПа) находится под действием продольных сил  (Рис. 2. 1). Требуется:
(Рис. 2. 1). Требуется:
1. Определить внутренние продольные силы  на каждом участке и построить их эпюру.
на каждом участке и построить их эпюру.
2. Построить эпюру нормальных напряжений  .
.
3. Определить полную абсолютную деформацию бруса.
4. Определить перемещение заданного сечения бруса I – I.
Данные взять в таблице 2. 1.
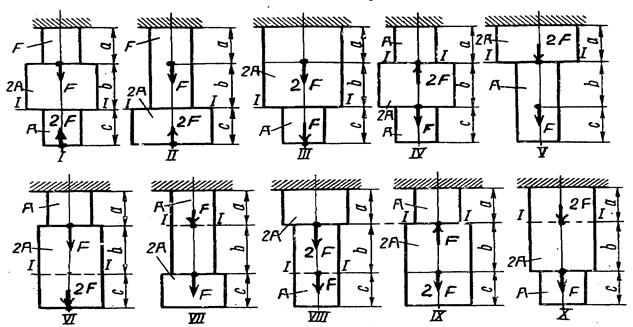
Рис. 2. 1.
ЗАДАЧА 2
Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержнем при помощи шарниров (рис. 2. 2). Требуется:
1. Найти усилия и напряжения в стержнях, выразив их через силу 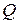 ;
;
2. Найти допускаемую нагрузку  , приравняв большее из напряжений в двух стержнях допускаемому напряжению [
, приравняв большее из напряжений в двух стержнях допускаемому напряжению [  ] =160 МПа;
] =160 МПа;
Данные взять из табл. 2. 1.
Таблица 2. 1.
| № строки | Схема по рис. 2. 1, 2. 2, 2. 3. | А·104 м2 | а | b | c | F, кН | Напряжение, МПа | |||||
| м | 
|
| 
| |||||||||
| I | 2, 1 | 2, 1 | 1, 1 | 1, 1 | ||||||||
| II III IV V VI VII VIII IX X | 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 82, 9 3, 0 | 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 82, 9 3, 0 | 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | ||||||||
| в | б | а | б | б | в | а | б | в | ||||
ЗАДАЧА 3
Стальной кубик (рис. 2. 3) находится под действием сил, создающих плоское напряженное состояние (одно из трех главных напряжений равно нулю). Требуется найти:
1. Главные напряжения и направления главных площадок;
2. Максимальные касательные напряжения, равные наибольшей полуразности главных напряжений;
3. Относительные деформации  ;
;
|
|
|
4. Относительное изменение объема:
5. Удельную потенциальную энергию деформации.
Данные взять из таблицы 2. 1.
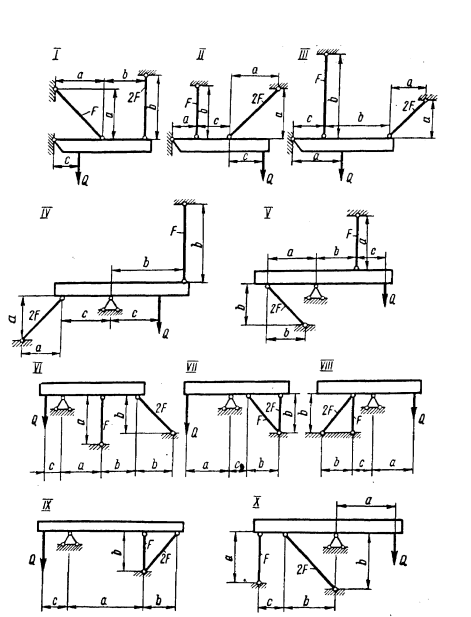
Рис. 2. 2
ЗАДАЧА 4
К стальному валу приложены три известных момента:  (рис. 2. 4. ). Требуется:
(рис. 2. 4. ). Требуется:
1. Установить, при каком значении момента Х угол поворота правого концевого сечения вала равен нулю;
2. Для найденного значения Х построить эпюру крутящих моментов;
3. При заданном значении [ 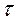 ] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 45, 50, 60, 70, 80, 90, 100 мм;
] определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 45, 50, 60, 70, 80, 90, 100 мм;
4. Построить эпюру углов закручивания;

Рис. 2. 3.
Таблица 2. 2.
| № строки | Схема по рис. 2. 4. | Расстояния, м | Моменты, кН·м | [ | ||||
| а | b | c | 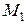
| 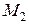
| 
| |||
| I II III IV V VI VII VIII IX X | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | |||||
| в | а | б | в | а | s | в | в | |
5. Найти наибольший относительный угол закручивания (на 1 пог. м).
Данные взять из табл. 2. 2.

Рис. 2. 4.
ЗАДАЧА 5
Для заданного в табл. 2. 3 поперечного сечения, состоящего из швеллера и равнобокого уголка или из двутавра и равнобокого уголка, или швеллера и двутавра (рис. 2. 5), требуется:
1. Определить положение центра тяжести;
2. Найти величины осевых (экваториальных) и центробежных моментов инерции относительно случайных осей, проходящих через центр тяжести (  и
и  );
);
3. Определить направление главных центральных осей (  и
и  );
);
4. Найти величины моментов инерции относительно главных центральных осей.
Указание: При расчете все необходимые данные следует брать из таблиц сортамента и ни в коем случае не заменять части профилей прямоугольниками.
|
|
|
Таблица 2. 3.
| № строки | Тип сечения по рис. 2. 5 | Швеллер | Равнобокий уголок | Двутавр |
| I II III IV V VI VII VIII IX X | 80 х 80 х 8 80 х 80 х 6 90 х 90 х 8 90 х 90 х 7 90 х 90 х 6 100 х 100 х 8 100 х 100 х 10 100 х 100 х 12 125 х 125 х 10 125 х 125 х 12 | 20а 22а 24а | ||
| в | а | б | в |
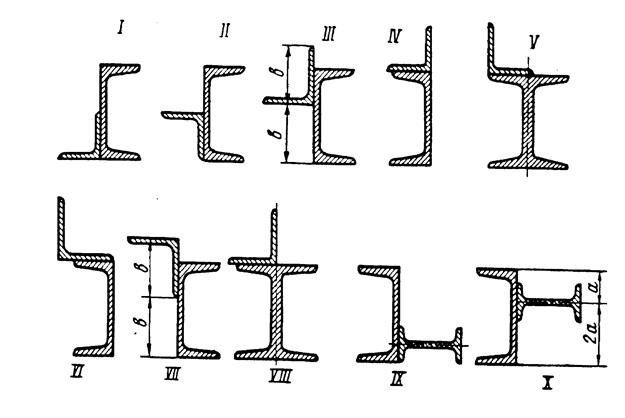
Рис. 2. 5.
ЗАДАЧА 6
Для заданных двух схем балок (рис. 2. 6) требуется написать выражения 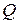 и
и  для каждого участка в общем виде, построить эпюры
для каждого участка в общем виде, построить эпюры 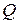 и
и  , найти
, найти  и подобрать: а) для схемы (а) деревянную балку круглого поперечного сечения при [
и подобрать: а) для схемы (а) деревянную балку круглого поперечного сечения при [  ] = 8 МПа; б) для схемы (б) стальную балку двутаврого поперечного сечения при [
] = 8 МПа; б) для схемы (б) стальную балку двутаврого поперечного сечения при [  ] = 160 МПа.
] = 160 МПа.
Данные взять из табл. 2. 4.
Таблица 2. 4
| № строки | Схема по рис. 2. 6. | 
|
| Расстояние в долях пролета | М, кН·м | Сосредоточенная сила |
| |||
| м | м | 
| 
| 
| ||||||
| I II III IV V VI VII VIII IX X | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | 0, 1 0, 2 0, 3 0, 5 0, 7 0, 6 1, 0 0, 8 0, 9 1, 0 | 0, 9 0, 8 0, 7 0, 6 0, 5 0, 6 0, 7 0, 8 0, 9 1, 0 | 0, 1 0, 2 0, 3 0, 4 0, 5 0, 1 0, 2 0, 3 0, 4 0, 5 | ||||||
| в | б | в | а | б | в | а | б | в | ||

Рис. 2. 6
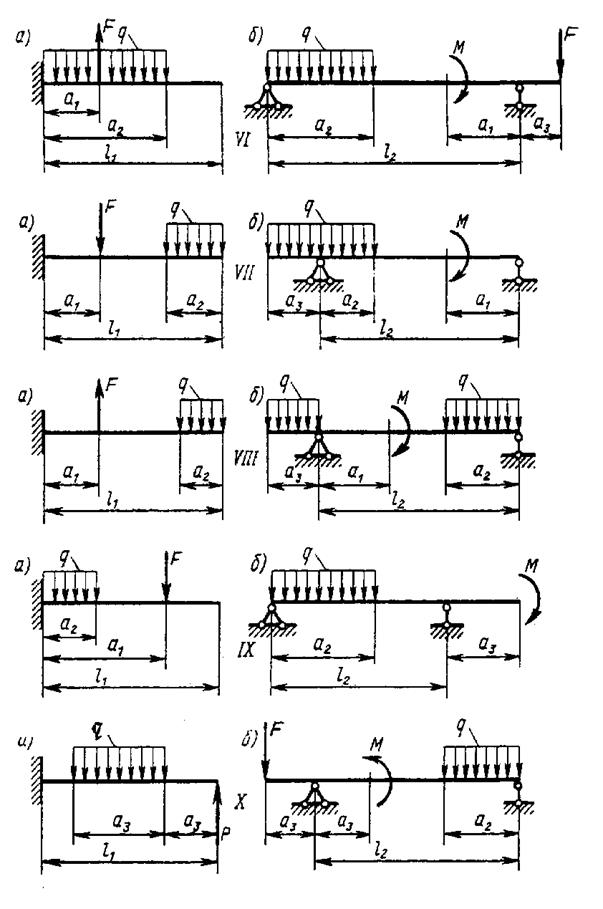
Рис. 2. 6 (продолжение)
ЗАДАЧА 7
Чугунный, короткий стержень, поперечное сечение которого изображено на рис. 2. 7, сжимается продольной силой 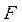 , приложенной в точке А.
, приложенной в точке А.
Таблица 2. 5
Требуется: 1. Вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через 2. Найти допускаемую нагрузку Данные взять из табл. 2. 5. |
| № строки | Схема по рис. 2. 7 | а | b | 
| 
| |||
| см | МПа | |||||||||
| I II III IV V VI VII VIII IX X | ||||||||||
| в | а | б | в | б | ||||||
|
|
|
Рис. 2. 7
ЗАДАЧА 8
Шкив с диаметром  и с углом наклона ветвей ремня к горизонту
и с углом наклона ветвей ремня к горизонту  делает
делает  оборотов в минуту и передает мощность
оборотов в минуту и передает мощность 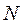 кВт. Два других шкива имеют одинаковый диаметр
кВт. Два других шкива имеют одинаковый диаметр  и одинаковые углы наклона ветвей ремня к горизонту
и одинаковые углы наклона ветвей ремня к горизонту 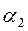 и каждый из них передает мощность
и каждый из них передает мощность 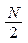 (рис. 2. 8). Требуется: 1. Определить моменты, приложенные к шкивам, по заданным величинам
(рис. 2. 8). Требуется: 1. Определить моменты, приложенные к шкивам, по заданным величинам 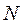 и
и 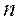 ; 4, построить эпюру крутящих моментов
; 4, построить эпюру крутящих моментов  . 2. Определить окружные усилия
. 2. Определить окружные усилия 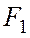 и
и 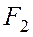 и давления на вал, действующие на шкивы, по найденным моментам и заданным диаметрам шкивов
и давления на вал, действующие на шкивы, по найденным моментам и заданным диаметрам шкивов  и
и  ; 3. Определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкивов и вала не учитывать); 4. Построить эпюры изгибающих моментов от горизонтальных сил
; 3. Определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях (вес шкивов и вала не учитывать); 4. Построить эпюры изгибающих моментов от горизонтальных сил 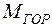 и от вертикальных сил
и от вертикальных сил 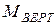 ; 5. Построить эпюру суммарных изгибающих моментов, пользуясь формулой:
; 5. Построить эпюру суммарных изгибающих моментов, пользуясь формулой: 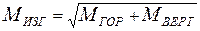 . 6. При помощи эпюр
. 6. При помощи эпюр  (см. п. 2 и
(см. п. 2 и 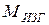 см. п. 7. Найти опасное сечение и определить величину максимального расчетного момента (по третьей теории прочности); 8. Подобрать диаметр вала
см. п. 7. Найти опасное сечение и определить величину максимального расчетного момента (по третьей теории прочности); 8. Подобрать диаметр вала 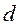 при [
при [  ] = 70 МПа и округлить его величину (см. задачу 4).
] = 70 МПа и округлить его величину (см. задачу 4).
Внимание! Студенты дистанционной формы обучения независимо от заданного варианта задачи принимают: значение угла  равным 0 градусов (горизонтальная плоскость), а значение угла
равным 0 градусов (горизонтальная плоскость), а значение угла 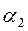 - девяносто градусам ( вертикальная плоскость).
- девяносто градусам ( вертикальная плоскость).
Данные взять из табл. 2. 6.
ЗАДАЧА 9
Стальной стержень длиной 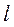 сжимается силой
сжимается силой 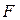 . Требуется:
. Требуется:
1. Найти размеры поперечного сечения при допускаемом напряжении на простое сжатие [  ] = 160 МПа (расчет производить последовательными приближениями, предварительно задавшись коэффициентом
] = 160 МПа (расчет производить последовательными приближениями, предварительно задавшись коэффициентом 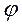 = 0, 5);
= 0, 5);
2. Найти критическую силу и коэффициент запаса устойчивости.
Данные взять из табл. 2. 7.
Таблица 2. 6
| № строки | Схема по рис. 3. 10 |
|
об/мин
| а | b | c | 
| 
|
|
|
| м | ||||||||||
| I II III IV V VI VII VIII IX X | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 1, 0 | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 1, 0 | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 1, 0 | 1, 1 1, 2 1, 3 1, 4 1, 5 0, 6 0, 7 0, 8 0, 9 1, 0 | 1, 1 1, 2 1, 3 1, 4 1, 5 0, 6 0, 7 0, 8 0, 9 1, 0 | |||||
| в | б | в | а | б | в | б | в | б | в | |
|
|
|
Рис. 2. 8
ЗАДАЧА 10
На рис. 2. 9 изображена нагруженная в своей плоскости рама, вертикальные элементы которой имеют моменты инерции I, а горизонтальные элементы -  ; 1) установить степень статического неопределимости и выбрать основную систему; 2) написать канонические уравнения; 3) построить эпюры
; 1) установить степень статического неопределимости и выбрать основную систему; 2) написать канонические уравнения; 3) построить эпюры  от единичных и от заданной нагрузки; 4) найти перемещения; 5) найти величины лишних неизвестных; 6) построить окончательные эпюры внутренних силовых факторов
от единичных и от заданной нагрузки; 4) найти перемещения; 5) найти величины лишних неизвестных; 6) построить окончательные эпюры внутренних силовых факторов  ,
,  и
и  . Данные взять из табл. 2. 8.
. Данные взять из табл. 2. 8.
Таблица 2. 7

Таблица 2. 8
| № строки | Схема рамы | 
| 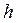
|
|
|
| м | |||||
| I II III IV V VI VII VIII IX X | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | ||||
| в | а | б | в | б | |

Рис 2. 9
|
|
|



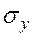

 , кН
, кН , кН/м
, кН/м
 ] и на растяжение [
] и на растяжение [ 


 , кН/м
, кН/м