3.7. Внецентренное растяжение и сжатие короткого бруса

 (к контрольной задаче № 7)

 

Сложным сопротивлением называют такой вид сопротивления стержней, когда мы имеем дело с комбинацией простейших деформаций.         

В поперечном сечении внецентренно сжатого бруса возникают нормальные напряжения , которые определяются следующей формулой:

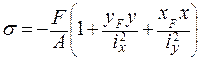                            ,                       (3. 21)

где F - приложенная нагрузка (Н);

 - площадь поперечного сечения колонны (м²);

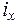,  - радиусы инерции сечения относительно главных центральных осей (м);

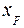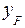,  - координаты точки приложения продольной силы (м);

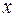,  - координаты точки сечения, в которой определяется напряжение (м).

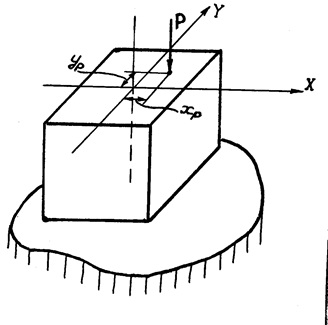Максимальные нормальные

 напряжения возникают в точках сечения наиболее удаленных от нулевой (нейтральной) линии. Насамой же линии нормальные напряжения равны нулю. Поэтому, если в уравнении (3. 21) принять  = 0, то мы получим уравнение нулевой линии:

, (3. 22)

здесь 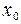,  - координаты точек                  

нулевой линии.

        Рис. 3. 13

Уравнение (3. 22), это уравнение прямой, не проходящей через начало координат. Если в этом уравнении принять 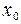 = 0, то получим величину отрезка, который нулевая линия отсекает на оси , если же принять  = 0, то получим величину отрезка, который нулевая линия отсекает на оси 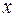, т. е.:

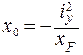                                            , .      (3. 23) Пример № 13. В сечении, указанном на рис. 3. 14 и принадлежащему внецентренно сжатой колонне, определить наиболее опасные точки и напряжения в них. Сжимающая сила  = 200 кН = 20 т приложена в точке .

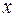Решение: Так как оси  и  являются осями симметрии – то они главные центральные оси.   

Наиболее опасными точками будут точки, в которых возни-ают максимальные нормаль-ные напряжения, а это точки – наиболее удаленные отнулевой линии. Следовательно, нам необходимо сначала определить положение нулевой линии. Записываем уравнение нулевой линии (3. 22).

   В нашем случае координаты точки приложения силы следующие (см. рис. 3. 14):

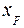 = – 90 мм = – 0, 09 м;  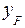= – 60 мм = – 0, 06 м;

Квадраты радиусов инерци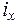и  и  определяются так:

                                        , ,                            (3. 24)

здесь 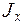 и 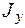 - осевые моменты инерции относительно главных центральных осей X и Y.

Определение осевых моментов инерции – см. конспект лекций раздел 8. «Геометрические характеристики сечений». Для нашего сечения будем иметь:

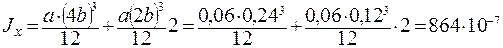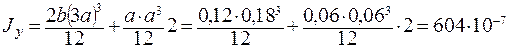м⁴,

м⁴,

Площадь всего сечения будет равна

м²;

и тогда квадраты радиусов инерции

м²; м².

 

     По формулам (3. 23) определим отрезки, которые нулевая линия отсекает на осях X  и Y:

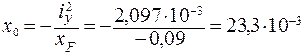м; м.

     Отложим эти отрезки на координатных осях, получим точки, в которых нулевая линия пересекает координатные оси. Через эти точки проводим прямую (см. рис. 3. 14). Видим, что наиболее удаленные точки, это точка  в зоне отрицательных напряжений и точка 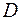 в зоне положительных напряжений.

     Определим напряжения в этих точках. По формуле (3. 21) имеем:

;

     С чертежа (рис. 3. 14) получим:

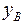 = – 0, 12 м;  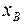= – 0, 03 м;

Тогда: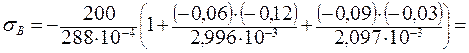   

= –5, 39× 10⁴ кН/м² = – 53, 9 МПа.

;

 = 0, 12 м; 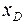 = 0, 03 м.

 = 1, 86× 10⁴ кН/м² =

= 18, 6 МПа.

Пример № 14. Чугунный короткий стержень, поперечное сечение которого изображено на рис. 3. 15, сжимается продольной силой F, приложенной в точке А.

Требуется: I) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих напряжений через F и размеры сечения; а = 40 мм, b = 60 мм;

2) найти допускаемую нагруз­ку F при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие 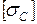= 100 МПа и на растяжение  = 30 МПа.

Решение: Выше указывалось, что геометрические характеристики  в  рас-

четных формулах берутся отно­ситель-

но главных центральных осей, поэтому

определим центр тяжести сечения. Ось X является осью сим­метрии и, следовательно, она про­ходит через центр тяжести, поэто­мунам достаточно найти его место­положение на этой оси. Разобьем сечение на два составных (1 и 2) и выберем вспомогательные

оси . Запишем коор­динаты цент-

 ров тяжести С₁ и С₂ в этих осях.   

          Рис. 3. 15                 Будем иметь С₁ (0, 0); С₂(0, 04; 0), тогда

 м;  = 0.

Итак, в осях xy₁  центр тяжести всего сечения имеет координаты С(0, 0133; 0). Проводим через центр тяжести сечения ось Y, перпен-дикулярную оси X. Оси X и Y и будут главными центральными осями сечения.

Определим положение нулевой линии. Дляэтого воспользуемся уравнением (3. 23)

, .

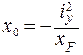Координаты точки приложения силы (точки А) будут следующие:  = (0, 02 – 0, 0133) + 0, 04 = 0, 0467 м;  = 0, 06 м;

Квадраты радиусов инерции определим как и в примере № 13 по формулам (3. 24):

,   .

 м⁴,

 м⁴,

где:  = 0. 0133 м;

 = 0, 04× 0, 24 + 0, 04× 0, 12 = 144× 10^-4 м².

 

 м²,    м²;

и тогда согласно формулы (3. 23) получим отрезки, отсекаемые нейтральной осью на главных осях инерции X и Y, соответственно:

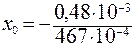 = – 10, 3× 10^-3 м,  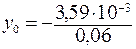= – 59, 8·10^-3 м.

     Откладываем на оси 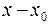, а на оси  и проводим через полученные точки нулевую линию (рис. 3. 15). Видим, что наиболее удаленные точки сечения от нулевой линии, это точка А в сжатой зоне и точка В в растянутой зоне. Координаты этих точек следующие: А (0, 0467; 0, 06); В (– 0, 0333; –0, 12). Определим по формуле (3. 21) напряжения в этих точках, выразив их через F.

= – 451, 6F,

 

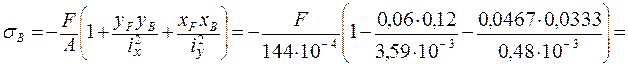
= – 291, 7F.

     Напряжение в точке А не должно превышать допускаемое напряжение на сжатие 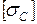, а напряжение в точке В не должно превышать допускаемого напряжения на растяжение , т. е. должны выполняться условия:

, .

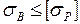или

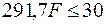, (а) . (б)

из (а): 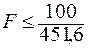          = 0, 221 МН = 221 кН;

из (б):           = 0, 103 МН = 103 кН.

     Чтобы одновременно удовлетворить условие прочности и в растянутой и в сжатой зонах колонны, мы должны взять в качестве допускаемой нагрузки меньшую из двух полученных, т. е.  = 103 кН.

3. 8 Расчет вала при совместном действии изгиба и кручения

(к контрольной задаче №8)

 

При известной мощности, передаваемой на вал, и числе оборотов вала n, скручивающий момент, действующий на вал, определяется так:

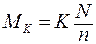                                                     .                                      (3. 25)

Если мощность N задается в лошадинных силах, а число оборотов n в об/мин, то K = 716, 2 и

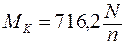                                      (кГм)                         (3. 26)

Если мощность N задается в кВт, а число оборотов n в об/мин, то K = 973, 6 и

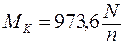                                      (кГм)                         (3. 27)

Если мощность N задается в кВт, а число оборотов в рад/с (обычно в этом случае число оборотов обозначается ), то K = 1 и

                                           (кНм).                            (3. 28)                     

Пример № 15. Шкив с диаметром 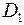 = 1 м и углом наклона ветвей к горизонту  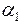=40° делает n = 600 об/мин и пере­дает мощность N₁ = 60 кВт. Два других шкива имеют одинаковый диа­метр  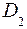=  = 0, 8 м и одинаковые углы наклона ветвей ремня к горизонту 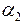=60° и каждый из них передает мощность  (рис. 3. 16, а). Требуется подобрать диаметр вала при [s] = 700 кГс/см² = 70  МПа.

1. Выясним какие виды деформации испытывает вал.

     Для этого усилия, которые приложены к шкиву (например, шкиву с диаметром 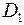) приведем к оси вала (рис. 3. 17). Перенос усилий 2t₁ и t₁, к оси вала требует приложения таких же усилий в противополож­ном направлении. Тогда усилия, перечеркнутые одной чертой, образуют пару с моментом , а усилия, перечеркнутые двумя чертами образуют пару с моментом . Суммарно эти моменты дают скручивающий момент

 

.

 

                         

 Рис. 3. 16                                        Рис. 3. 17

 

 

Кроме того, на вал передается усилие, действующее перпендикулярно оси вала и по величине равное F₁ = 2t₁ + t₁ = 3t₁. Скручивающий момент  вызывает деформацию кручения, а усилие F ₁ – дефор­мацию изгиба. Таким образом, имеем совместное действие изгиба с кручением и, следовательно, для подбора диаметра необходимо исполь­зовать гипотезы прочности. Так как вал изготовлен из пластичного ма­териала, воспользуемся третьей гипотезой прочности, согласно которой

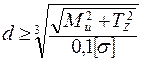                                     .                       (3. 26)

Анализируя эту формулу видим, что нам необходимо определить скручивающие моменты, передаваемые на вал каждым шкивом, и выяснить харак­тер распределения крутящих моментов по длине вала, т. е. построить эпюру крутящих моментов (эп. ). Кроме того, для выяснения харак­тера распределения изгибающих моментов по длине вала, т. е. для построения эпюры изгибающих моментов (эп. ) нам необходимо опре­делить усилия, которые действуют на вал перпендикулярно оси вала. Имея эп.  и эп.  мы сможем выяснить, в каком сечении совместное действие изгиба и кручения наиболее опасно, т. е. для какого сече­ния выражение  будет наибольшим в формуле (3. 26). Для это­го опасного сечения мы и подберем диаметр.

 Итак, приступаем к решению задачи.

1. Определим по формуле (3. 24) скручивающие моменты, передаваемые шкивами на вал:

 = 97, 4 кГм = 974× 10^-3 кНм,

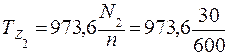 = 48, 7 кГм = 487× 10^-3 кНм.

2. По полученным данным строим эпюру крутящих моментов. Так как знак крутящего момента выбирается произвольно, то примем кру­тящий момент, возникающий от действия скручивающего момента  положительным. Тогда эп.  будет иметь вид, указанный на рис. 3. 16, б.

3. Определим окружные усилияt₁, t₂ и t₃, воспользовавшись выводом, полученным в пункте 1 настоящей задачи:

                                              , отсюда

 = 194, 8 кГ = 1, 95 кН.

Аналогично 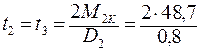 = 121, 8 кГ = 1, 22 кН.

4. Определим давления на вал:

а) горизонтальная плоскость

 = 3× 194, 8 = 584, 4 кГс = 5, 84 кН; (см. пункт 1 настоящей задачи);

б) вертикальная плоскость  = 3× 121, 8 = 365, 4 кГс = 3, 65 кН.

5. Так как усилия  и  действуют в разных плоскостях, то

спроектируем их на горизонтальную и вертикальную оси (рис. 3. 18, а, б)

                  а)                                                            б)                   

Рис. 3. 18.

 = –584, 4× 0, 766 = –447, 6 кГ = –4, 48 кН,

= –584, 4× 0, 643 = –375, 8 кГ = –3, 76 кН,

 = 365, 4× 0, 5=182, 7 кГ = 1, 83 кН,

= –365, 4× 0, 87 = –316, 4 кГ = –3, 16 кН.

      Примечание: пункт 5 не выполняют студенты дистанционной формы обучения, т. к. углы наклона ветвей к горизонту для них принимаются: 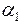 = 0º ;  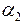= 90º .  

     6. Построим эпюры изгибающих моментов от горизонтальных сил (эп. 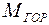) и от вертикальных сил (эп. 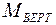). Рассмотрим горизонтальную плоскость. Для этого представим вал как балку на двух опорах (опоры ставим в местах установки подшипников) и нагрузим ее силами, действующими в горизонтальной плоскости. Так как силы Х₁ и Х₂, Х₃ имеют разные знаки, то и приложить на балку их надо так, чтобы они действовали в разные стороны. Напрвниз, а Х₂ и Х₃ – вверх (см. рис. 3. 16, в) или наоборот, для решения задачи это несущественно.

     Определим реакции опор Х_А  и Х_В (рис. 3. 16, в):

; – Х₂× 0, 4 – Х₁× 0, 3 + Х_В× 0, 9 + Х₃× 1, 1 = 0;

 = 7, 1 кГ = 71× 10^-3 кН.

; ;

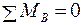 = 75, 1 кГ = 751× 10^-3 кН.

Проверка: 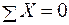         ; 182, 7 + 75 – 447, 6 + 7 + 182, 7 = 0;

447, 6 – 447, 6 = 0.

     Определим изгибающие моменты в сечениях С, А, D, В, Е, т. е. на границах силовых участков

М_С = 0; М_А = 182, 7× 0, 4 = 73, 1 кГм = 0, 731 кНм;

M_D = 182, 7× 0, 7 + 75, 1× 0, 3 = 150, 4 кГм = 1, 5 кНм;

М_Е = 0; М_В = 182, 7× 0, 2 = 36, 5 кГм = 0, 365 кНм.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: