 |
3.2. Статически неопределимые задачи на
|
|
|
|
3. 2. Статически неопределимые задачи на
растяжение и сжатие
(к контрольной задаче № 2)
П ример № 4. Для абсолютно жесткого бруса, опирающегося на шарнорно неподвижную опору и прикрепленного к двум стержням (рис. 3. 4) требуется: 1. Найти усилия и напряжения в стержнях, выразив их через силу Q; 2. Найти допускаемую нагрузку 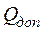 , если
, если 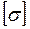 = 160 МПа =1600 кг/см2,
= 160 МПа =1600 кг/см2, 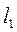 =
=  =
=  = 2 м, a = b = c = 2 м,
= 2 м, a = b = c = 2 м,  = 10 см2,
= 10 см2, 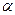 = 45º.
= 45º.
Решение: 1. Найдем усилия в стержнях, выразив их через неизвестную силу Q.
Составим уравнения статического равновесия (рис. 3. 4, а):
 ;
; 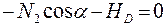 ; (3. 2)
; (3. 2)

а) б)
Рис. 3. 4
 ;
;  ; (3. 3)
; (3. 3)
 ;
; 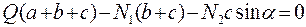 . (3. 4)
. (3. 4)
Задача один раз статически неопределима, т. к. имеет четыре неизвестных (N1, N2, RD, HD) и три уравнения статического равновесия. Составим дополнительное уравнение.
Условие совместности перемещений получим, представив систему в деформированном состоянии – положение 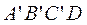 (рис. 3. 4, б). Из подобия треугольников
(рис. 3. 4, б). Из подобия треугольников 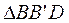 и
и 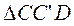 следует:
следует:
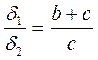 , (3. 5)
, (3. 5)
но  , а из треугольника
, а из треугольника 
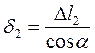
Подставив 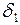 и
и 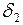 в (3. 5), получим:
в (3. 5), получим:
 или
или 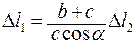 (3. 6)
(3. 6)
Из закона Гука 
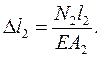
Тогда (3. 6) примет вид:  .
.
Подставив исходные данные, получим:
 (3. 7)
(3. 7)
Решая совместно (3. 4) и (3. 7), вычисляем 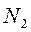 :
:
 ;
;  ;
;
из (3. 4): 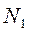 = 2, 83
= 2, 83 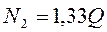 .
.
Определим напряжения в стержнях:
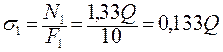 ;
;  (3. 8)
(3. 8)
2. Определим допускаемую нагрузку 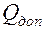 . Так как в нашем случае
. Так как в нашем случае  , то приравняв
, то приравняв  , получим с учетом (3. 8):
, получим с учетом (3. 8):
|
|
|
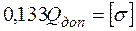 ,
,
 = 12× 103 кг = 120 кН. (3. 9)
= 12× 103 кг = 120 кН. (3. 9)
3. 3. Элементы теории напряженного и деформированного
состояния
(к контрольной задаче № 3)
Пример № 5. Для элементарного объема (рис. 3. 5), находящегося под действием сил, создающих плоское напряженное состояние, требуется вычислить: 1) главные напряжения и положение главных площадок; 2) максимальные касательные напряжения, если 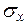 = 40 МПа = 400 кг/см2,
= 40 МПа = 400 кг/см2, 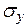 = 20 МПа = 200 кг/см2,
= 20 МПа = 200 кг/см2, 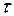 = 10 МПа= 100 кг/см2.
= 10 МПа= 100 кг/см2.
 |
1) Вычисляем главные напряжения по формуле:

 = 441 кг/см2 = 44, 1 Мпа;
= 441 кг/см2 = 44, 1 Мпа;  = 159 кг/см2 = 1, 59 МПа.
= 159 кг/см2 = 1, 59 МПа.
Учитывая, что между главными напряжениями существует зависимость  >
>  >
> 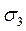 , получим
, получим  =
=  = 44, 1 МПа;
= 44, 1 МПа;  =
=  = 1, 59 МПа;
= 1, 59 МПа; 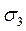 = 0.
= 0.
Положение главных площадок определяем по формуле:
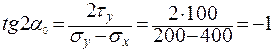 ;
; 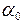 = –22, 5º.
= –22, 5º.
Знак перед  , принимают согласно правила (рис. 3. 5, б).
, принимают согласно правила (рис. 3. 5, б).
Учитывая, что положительный угол отсчитывается от оси против часовой стрелки, а отрицательный – по часовой стрелке, откладываем от направления напряжения 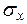 углы
углы 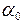 = –22, 5º и
= –22, 5º и  = (90º – 22, 5)° и, проведя оси, строим на этих осях главные площадки и показываем главные напряжения (рис. 3. 5, а).
= (90º – 22, 5)° и, проведя оси, строим на этих осях главные площадки и показываем главные напряжения (рис. 3. 5, а).
При этом  =
=  – направлено в тот квадрант, где касательные напряжения
– направлено в тот квадрант, где касательные напряжения  и
и  сходятся к ребру.
сходятся к ребру.
2) Вычислим максимальные касательные напряжения по формуле:
 = ±141 кг/см2 = ±14, 1 МПа.
= ±141 кг/см2 = ±14, 1 МПа.
Пример № 6. Стальной кубик (рис. 3. 6) находится под действием сил, создающих плоское напряженное состояние. Требуется найти:
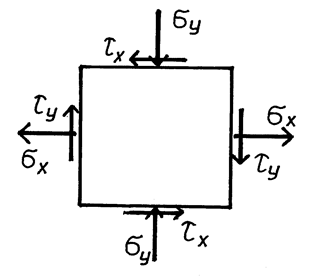 Рис. 3. 6
Рис. 3. 6
| 1) относительные деформации 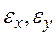 и и 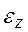 ; 2) относительное изменение объема; 3) удельную потенциальную энергию деформации, если ; 2) относительное изменение объема; 3) удельную потенциальную энергию деформации, если 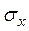 =50 МПа = 500 кг/см2, =50 МПа = 500 кг/см2, 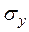 = 40 МПа = 400 кг/см2, = 40 МПа = 400 кг/см2,  = 20 МПа = 200 кг/см2. Модуль продольной упругости Е = 2× 105 МПа = 2× 106 кг/см2, модуль сдвига G = 8× 104 МПа = 8× 105 кг/см2. = 20 МПа = 200 кг/см2. Модуль продольной упругости Е = 2× 105 МПа = 2× 106 кг/см2, модуль сдвига G = 8× 104 МПа = 8× 105 кг/см2.
|
Решение: 1. Рассчитаем относительные деформации 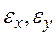 и
и 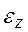 . Примем для стали коэффициент Пуассона
. Примем для стали коэффициент Пуассона 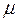 = 0, 3. Учтем, что согласно рис. 3. 6:
= 0, 3. Учтем, что согласно рис. 3. 6: 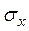 = +500 кг/см2,
= +500 кг/см2, 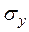 = - 400 кг/см2,
= - 400 кг/см2,  =0,
=0, 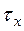 = –200 кг/см2,
= –200 кг/см2,  = +200 кг/см2,
= +200 кг/см2,  = 2·106 кг/см2,
= 2·106 кг/см2, 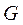 = 8·105 кг/см2. Тогда получим, используя формулу обобщенного закона Гука:
= 8·105 кг/см2. Тогда получим, используя формулу обобщенного закона Гука:
|
|
|
 ;
;
 ;
;
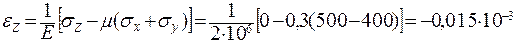 .
.
2. Вычислим относительное изменение объема по формуле

или
 .
.
3. Вычислим удельную потенциальную энергию деформации для двухосного напряженного состояния (  =0) по формуле:
=0) по формуле:
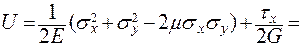
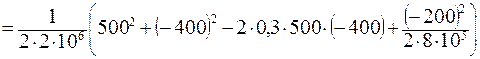 = 0, 157
= 0, 157 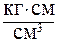 = = 0, 157× 105
= = 0, 157× 105 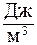 .
.
3. 4. Расчет вала круглого поперечного сечения
на прочность и жесткость
(к контрольной задаче № 4)
Пример № 7. Для заданного вала, находящегося в равновесии, и нагруженного как показано на рис. 3. 7, построить эпюру крутящих моментов, если  = 2000 Нм = 200 кг·м,
= 2000 Нм = 200 кг·м,  = 2500 Нм = 250 кг·м,
= 2500 Нм = 250 кг·м, 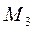 = 1000 Нм = 100 кг·м,
= 1000 Нм = 100 кг·м, 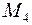 = 1500 Нм = 150 кг·м, а = 1 м.
= 1500 Нм = 150 кг·м, а = 1 м.
Решение: Вспомним правило знаков: внутренний крутящий момент  в произвольном сечении бруса положителен, если внешний крутящий момент стремится повернуть отсеченную часть вала против часовой стрелки, если смотреть со стороны сечения.
в произвольном сечении бруса положителен, если внешний крутящий момент стремится повернуть отсеченную часть вала против часовой стрелки, если смотреть со стороны сечения.
Применим метод сечения, учитывая, что внутренний крутящий момент в произвольном сечении бруса численно равен алгебраической сумме внешних крутящих моментов, приложенных к валу по одну сторону от этого сечения, т. е.:
 . (3. 10)
. (3. 10)
Разобьем вал на три участка, проведем произвольные сечения I, II и III и стрелками укажем направление взгляда на оставшуюся часть вала. Тогда, используя зависимость (4. 1), получим:
Участок АВ: 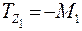 = –200 кг·м = –2·10-3 Нм.
= –200 кг·м = –2·10-3 Нм.
Участок ВС:  = –100 + 150 = +50 кг·м = 0, 5·103 Нм.
= –100 + 150 = +50 кг·м = 0, 5·103 Нм.
Участок СД:  =150 кг·м = 1, 5·103 Нм.
=150 кг·м = 1, 5·103 Нм.
Выбираем масштаб и строим эпюру  . Для проверки используем правило: в сечениях вала, где приложены внешние крутящие моменты, на эпюре
. Для проверки используем правило: в сечениях вала, где приложены внешние крутящие моменты, на эпюре  возникают скачки на величину этих моментов и в их направлении.
возникают скачки на величину этих моментов и в их направлении.

| 
|
Рис. 3. 7 Рис. 3. 8
Пример № 8. Проверить прочность стального вала, показанного на рис. 3. 7, если его диаметр d = 65 мм, а  = 40 МПа.
= 40 МПа.
Решение: Находим опасное сечение (сечение, в котором  ). Это любое поперечное сечение на участке АВ, где
). Это любое поперечное сечение на участке АВ, где 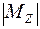 = 200 кг·м.
= 200 кг·м.
Согласно формулы условия прочности на кручение, получим:
|
|
|
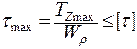 (3. 11)
(3. 11)
или
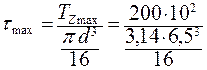 = 370 кг/см2 = 37 МПа.
= 370 кг/см2 = 37 МПа.
Прочность вала обеспечена.
Пример № 9. К стальному валу (  = 8·104 МПа = 8·105 кг/см2) приложен крутящий момент М = 7·103 Нм = 700 кг·м (рис. 3. 8).
= 8·104 МПа = 8·105 кг/см2) приложен крутящий момент М = 7·103 Нм = 700 кг·м (рис. 3. 8).
Требуется: 1. Установить при каком значении момента  угол поворота концевого сечения вала равен нулю; 2. Построить эпюру крутящих моментов с учетом найденного значения
угол поворота концевого сечения вала равен нулю; 2. Построить эпюру крутящих моментов с учетом найденного значения  ; 3. Определить диаметр вала, если
; 3. Определить диаметр вала, если  = 80 МПа = 800 кг/см2; 4. Построить эпюру углов закручивания; 5. Найти наибольший относительный угол закручивания (на 1 м), если а = 2 м = 200 см, b = 1, 5 м = 150 см.
= 80 МПа = 800 кг/см2; 4. Построить эпюру углов закручивания; 5. Найти наибольший относительный угол закручивания (на 1 м), если а = 2 м = 200 см, b = 1, 5 м = 150 см.
Решение: 1. Вал имеет два участка АВ и ВС. Проводим сечения I и II и определяем для каждого участка внутренний крутящий момент, начиная от свободного правого конца вала, чтобы не определять реактивный момент в заделке. Используя зависимость (3. 10), получим:
Участок СВ:  = –Х;
= –Х;
Участок ВА:  = –Х + М = 700 – Х. (3. 12)
= –Х + М = 700 – Х. (3. 12)
Угол закручивания 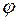 определяется по формуле:
определяется по формуле:
 (3. 13)
(3. 13)
Если вал имеет n участков, то угол закручивания его конечных сечений равен алгебраической сумме углов закручивания каждого i –го участка, т. е.
 (3. 14)
(3. 14)
Тогда, учитывая условие рассматриваемого пункта, что угол поворота сечения С относительно А равен нулю, запишем с учетом (3. 13) и (3. 14):
 ;
; 
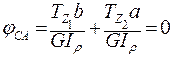 .
.
Подставив из (3. 12) значения  и
и 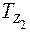 , получим после преобразований:
, получим после преобразований:
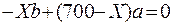 ; Х = 400 кг× м.
; Х = 400 кг× м.
2. Строим эпюру крутящих моментов на основании (3. 12) и (3. 15):
 = –Х = –400 кг× м = –4× 103 Нм,
= –Х = –400 кг× м = –4× 103 Нм,
 = –Х + М = –400 + 700 = 300 кг× м = 3× 103 Нм.
= –Х + М = –400 + 700 = 300 кг× м = 3× 103 Нм.
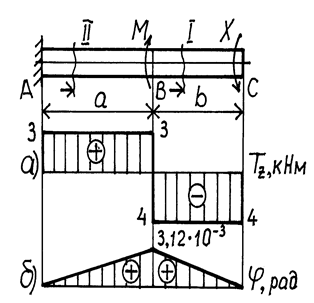
Выбираем масштаб и строим эпюру  (рис. 3. 8, а). Для ее проверки используем правило, представленное в примере № 7.
(рис. 3. 8, а). Для ее проверки используем правило, представленное в примере № 7.
3. Определяем диаметр вала из расчета на прочность. Опасное сечение на участке СВ:  = 4·103 Нм = 400 кг·м. Определяем диаметр вала по формуле, полученной из условия прочности (3. 11):
= 4·103 Нм = 400 кг·м. Определяем диаметр вала по формуле, полученной из условия прочности (3. 11):
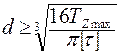 или
или  = 6, 3 см = 63× 10-3 м.
= 6, 3 см = 63× 10-3 м.
|
|
|
Согласно стандартного ряда, округляем: d = 70 мм.
4. Строим эпюру углов закручивания. Идем от неподвижного сечения вала А. Угол поворота сечения В относительно сечения А согласно формулы (3. 13):
 рад;
рад;
 см4.
см4.
Аналогично:
 рад.
рад.
Выбираем масштаб. На эпюре углов закручивания (рис. 3. 8, б) под сечением В откладываем значение  рад и соединяем полученную точку с началом координат. Затем под сечением С откладываем
рад и соединяем полученную точку с началом координат. Затем под сечением С откладываем 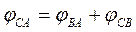 = 3, 12·10-3 – 3, 12·10-3 = 0, и строим эпюру
= 3, 12·10-3 – 3, 12·10-3 = 0, и строим эпюру 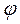 на участке СВ. Эпюра
на участке СВ. Эпюра 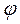 в сечении С пришла в ноль. Это говорит о том, что условие пункта 1 задачи выполнено и значение момента Х найдено правильно.
в сечении С пришла в ноль. Это говорит о том, что условие пункта 1 задачи выполнено и значение момента Х найдено правильно.
5. Определяем наибольший относительный угол закручивания  . Для каждого участка получим, поделив угол закручивания на его длину:
. Для каждого участка получим, поделив угол закручивания на его длину:
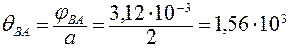 рад/м;
рад/м;
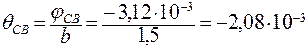 рад/м;
рад/м;
Отсюда  рад/м.
рад/м.
|
|
|


