По полученным результатам строим эпюру  (рис. 3.16,г). Рассмотрим вертикальную плоскость Показываем балку на двуопорах и нагрузим ее силами У1, У2 и У3 (рис. 3.16,д).

По полученным результатам строим эпюру  (рис. 3. 16, г). Рассмотрим вертикальную плоскость Показываем балку на двуопорах и нагрузим ее силами У1, У2 и У3 (рис. 3. 16, д).

     Определим реакции опор У_А и У_В:

 

; У₂× 0, 4 – У₁× 0, 3 + У_В× 0, 9 – У₃× 1, 1 = 0,

 = 371, 4 кГ = 3, 714 кН.

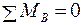; У₂× 1, 3 – У_А× 0, 9 + У₁× 0, 6 – У₃× 0, 2 = 0,

 = 637, 2 кГ = 6, 372 кН.

 

Проверка: 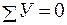; –316, 4 + 637, 2 – 375, 8 + 371, 4 – 316, 4 = 0,

1008, 6 – 1008, 6 = 0.

     Определим изгибающие моменты в сечениях С, А, D, В, Е.

М_С = 0; М_А = – 316, 4× 0, 4 = – 126, 6 кГм = – 1, 266 кНм;

   M_D = – 316, 4× 0, 7 + 637, 2× 0, 3 = – 30, 3 кГм = – 0, 303 кНм;

М_Е = 0; М_В = – 316, 4× 0, 2 = – 63, 3 кГм = –0, 633 кНм.

     По полученным результатам строим эпюру 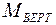 (рис. 3. 16, е).

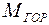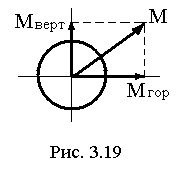
7. На основании эпюр  и 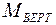 строим эпюру суммарного момента М. Суммарный момент в любом сечении вала можно определить, как геометрическую сумму моментов в вертикальной и горизонтальной плоскостях (рис. 3. 19).

 

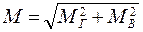, тогда М_С = 0;

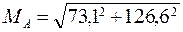 = 146, 1 кГм = 1, 46 кНм,

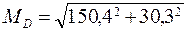 = 153, 4 кГм = 1, 53 кНм,

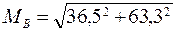 = 73, 1 кГм = 0, 73.                                        .                         

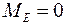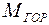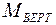   Суммарная будет прямолинейной на тех      участках вала, где  и  одновременно убывает или одновременно возрастают (по абсолютной величине). На тех участках где  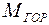возрастает, а  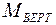убывает (или наоборот), эпюра суммарных моментов будет очерчиваться кривой линией без экстремумов. Эпюра суммарных моментов показана на рис. 3. 16, ж.

     8. Определим опасное сечение. Таковым, очевидно, будет сечение в месте посадки шкива с диаметром 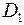, т. к. здесь мы имеем максимальный суммарный момент  = 153, 4 кГм и  = 48, 7 кГм (по кручению все сечения вала равноопасны, т. к. во всех сечениях крутящий момент одинаков).

     9. Определим диаметр вала по формуле (3. 26), взятой из конспекта:

 = 6, 13 см.

     Округляем диаметр до стандартной величины в большую сторону d = 70 мм.

 

3. 9. Устойчивость центрально сжатых стержней

(к контрольной задаче № 9)

 

     Критическая нагрузка при расчете на устойчивость аналогична разрушающей нагрузке при расчете на прочность. Если мы хотим создать известный запас устойчивости, должно быть соблюдено условие:

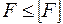                                        , где                           (3. 27)

где: F – действующая нагрузка;

     F_КР – критическая нагрузка;

    [F] – допускаемая нагрузка;

     K_У – коэффициент запаса устойчивости, для стали обычно берут K_У = 1, 7¸ 3.

     Критическая сила определяется или по формуле Эйлера

                                             ,                               (3. 31)    

или по формуле Ясинского:  

                                            ,                            (3. 32)

где Е – модуль Юнга;

     – осевой момент инерции поперечного сечения, минимальный;

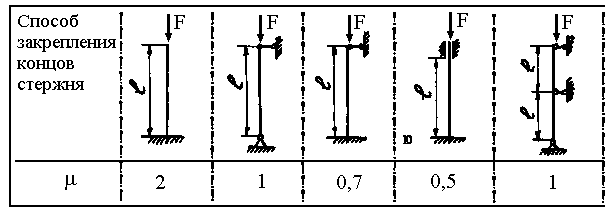
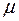     – коэффициент приведения длины, зависящий от способа крепления концов стержня.

     Значения коэффициента 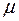 в формулах (3. 31) и (3. 32) в зависимости от способа закрепления приведены в таблице 3. 1. l – длина стержня, а и b – эмпирические коэффициенты Ясинского (для стали имеют следующие значения: а = 310 МПа, b = 1, 14 МПа);  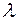– гибкость стойки, определяемая по формуле

                                                   ,                                      (3. 33)

где  – минимальный радиус инерции.

Таблица 3. 1

         

В зависимости от гибкости стойки применяют или формулу Эйлера (3. 31), или формулу Ясинского (3. 32). Так, если гибкость стойки больше или равна предельной гибкости, т. е. , то для определения критической силы применяют формулу (3. 28). В свою очередь предельная гибкость определяется так:

                                                ,                             (3. 34)

 

где 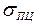 – предел пропорциональности материала стойки.

     Если же гибкость стойки меньше предельной, а напряжения не превышают предела текучести, то для определения критической силы применяют формулу (3. 32).

                                                                                               Таблица 3. 2

Гибкость	для
	сталей: Ст. 1, Ст. 2, Ст. 3, Ст. 4.	сталей Ст. 5	стали повышенного качества	чугуна	дерева
	1, 00	1, 00	1, 00	1, 00	1, 00
	0, 99	0, 98	0, 97	0, 97	0, 99
	0, 96	0, 95	0, 95	0, 91	0, 97
	0, 94	0, 92	0, 91	0, 81	0, 93
	0, 92	0, 89	0, 87	0, 69	0, 87
	0, 89	0, 86	0, 83	0, 57	0, 80
	0, 86	0, 82	0, 79	0, 44	0, 71
	0, 81	0, 76	0, 72	0, 34	0, 60
	0, 75	0, 70	0, 65	0, 26	0, 48
	0, 69	0, 62	0, 55	0, 20	0, 38
	0, 60	0, 51	0, 43	0, 16	0, 31
	0, 52	0, 43	0, 35	-	0, 25
	0, 45	0, 37	0, 30	-	0, 22
	0, 40	0, 33	0, 26	-	0, 18
	0, 36	0, 29	0, 23	-	0, 16
	0, 32	0, 26	0, 21	-	0, 14
	0, 29	0, 24	0, 19	-	0, 12
	0, 26	0, 21	0, 17	-	0, 11
	0, 23	0, 19	0, 15	-	0, 10
	0, 21	0, 17	0, 14	-	0, 09
	0, 19	0, 16	0, 13	-	0, 08

 

     Часто возникает необходимость в первую очередь определять не критическую силу, а по заданной нагрузке выбрать поперечное сечение стойки так, чтобы удовлетворялось условие устойчивости. Для этого служит формула, справедливая при любой гибкости:

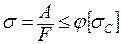                                                 ,                             (3. 35)

где 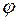 – коэффициент понижения основного допускаемого напряжения на сжатие.

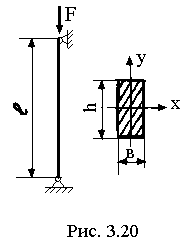
     Значения коэффициента 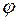 в зависимости от гибкости приведены в таблице 3. 2.

Пример № 16. Определить критическую силу для стального стержня (Е = 2·10⁵ МПа) прямоугольного сечения (рис. 3. 20), если размеры сечения: b=0, 06 м, h = 0, 1 м, длина стержня l = 3, 5 м.  

Решение: Определяем гибкость по формуле (3. 33) - .           

Вычисляем =  = 0, 0173 м

Коэффициент приведения длины 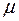 = 1 (см. таб. 3. 1). Тогда .

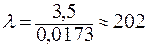     Вычисляем предельную гибкость для стали по формуле (3. 34)

 

 = » 100.

 

     Так как , то критическую силу надо считать по формуле Эйлера (3. 31):

 

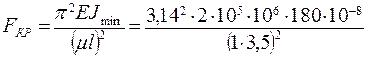 = 289, 7× 10³ Н = 290 кН,

где  = 180× 10^-8 м⁴.

 

     Расширим эту задачу и определим критическое напряжение:

 

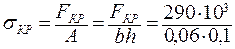 = 48, 3× 10⁶ Па = 48, 3 МПа.

     Таким образом, при гибкости стержня 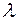 = 202 критическим оказалось напряжение, не только значительно меньшее предела пропорциональности (  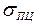= 200 МПа), но в три с лишним раза меньше допускаемого напряжения (  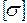= 160 МПа).

Пример № 17. Стальной стержень длиной l = 3 м сжимается силой F = 500 кН (рис. 3. 21). Требуется: 1) найти размеры поперечного сечения при допускаемом напряжении на простое сжатие 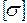 = 160 МПа; 2) найти критическую силу и коэффициент запаса устойчивости.

                                    Решение: Из формулы (3. 35) имеем

.

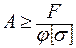Так как здесь ни площадь F, ни коэффициент снижения допускаемого напряжения 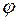 неизвестны, то расчет будем вести методом последовательного приближения.

В первом приближении, зная, что коэффициент 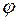  принимает значения от нуля до единицы, зададимся значением  = 0, 5. Чтобы нам на каждом этапе проводить меньше рутинной работы, выразим гибкость стойки 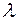 через площадь сечения А, т. е.

                                     , ,

 

Минимальный момент инерции:

,

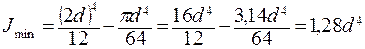Площадь поперечного сечения составного сечения

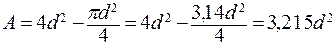                     ,                (3. 36)

 

Откуда:                               ,                                      (3. 37)

 

Минимальный радиус инерции:

.

Тогда для гибкости стойки получим формулу

                                       .                        (3. 38)

Первое приближение.  = 0, 5. Определим площадь поперечного сечения:

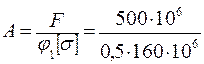 = 6, 25× 10^-3 м².

Определяем гибкость стойки по формуле (3. 38)

 = 72, 5.

     Обратимся к таблице 3. 2 и уточним значение коэффициента 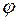 (обозначим его 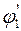) в соответствии с полученной гибкостью  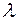= 72, 5. Так как точно для этой гибкости значения коэффициента нет, определим его воспользовавшись правилом линейного интерполирования. Делается это так: выпишем значения коэффициентов  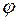(из второго столбца (табл. 3. 2), для сталей: Ст. 1, Ст. 2, Ст. 3, Ст. 4, соответствующих гибкостям  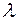= 70 и  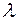= 80:                    

Замечаем, что при  изменении   l  на  10  единиц	l	j
изменилось на 0, 06. Наша же гибкость отличается от  = 70 на 2, 5 единицы. Какое изменение  приходится на эти 2, 5 единицы мы не знаем и обозначим через x.		0, 81
		0. 75

Итак, можем составить пропорцию 10: 2, 5 = 0, 06: х. Отсюда:

,

     Таким образом, при изменении 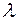 на 2, 5 единицы  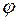изменяется на 0, 02. Тогда  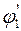= 0, 81 – 0, 02 = 0, 79.

Сравниваем  и

.

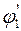
     Допускается расхождение не более чем на 5%; у нас же значительно больше 5%, поэтому переходим ко второму приближению:

 = 0, 645.

     Второе приближение. Определим площадь поперечного сечения

 = 4, 85× 10^-3 м².

Определяем гибкость стойки

 = 82, 3

Обращаемся к таблице 3. 2 и уточняем значение 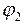. Действуем точно так же как на первом этапе приближения.

,  = 0, 01.

.

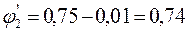Сравним 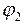 и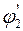

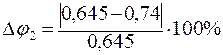 = 14, 7% > 5%.

Переходим к третьему приближению.

 = 0, 7.

     Третье приближение. Определим площадь поперечного сечения

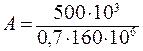 = 4, 46× 10^-3 м².

Определяем гибкость стойки

 = 85, 6.

Обращаемся к таблице 3. 2 и уточняем значение .

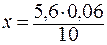, » 0, 03,

.

     Сравним  и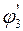

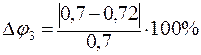 = 2, 86 % < 5 %.

     Отличие  в пределах допустимого.

     Принимаем стойку площадью А = 4, 46× 10^-3 м². Размер d этой стойки определим из формулы (3. 37):

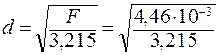 = 0, 0373 м,

а гибкость 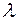 = 85, 6.

Определим величину критической силы.

     В задаче № 16 мы определили предельную гибкость для стали 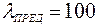. Таким образом, гибкость нашей стойки  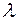= 85, 6 меньше предельной и, следовательно, критическую силу надо определять по формуле Ясинского (3. 29):

 = 948 кН.

     Определим коэффициент запаса устойчивости на основании формулы (3. 27):

 = 1, 90.

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: