 |
3.10. Расчет статически неопределимых систем методом сил
|
|
|
|
(к контрольной задаче № 10)
Пример № 18. Для заданной статически неопределимой рамы (рис. 3. 22, а) при заданных размерах и нагрузках, вертикальные элементы которой имеют осевой момент инерции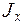 
горизонтальные - 2 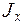, требуется: 1) установить степень статической неопределимости и выбрать основную систему; 2) написать канонические уравнения; 3) построить эпюры от единичной силы и заданных нагрузок; 4) найти перемещения; 5) найти величину лишних неизвестных; 6) построить окончательные эпюры N, Q и M.
Решение: 1. Для заданной системы устанавливаем степень статической неопределимости. Имеем четыре незвестных (RA, HA, RB и HB ) (рис. 3. 22, а) и три уравнения статики ( 
; 
; 
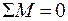). Тогда степень статической неопределимости (ССН) будет равна: ССН = n – y = 4 – 3 = 1,
где: n – число неизвестных; у – число уравнений статики, которые можно составить для заданной рамы.
Следовательно, для решения необходимо составить одно дополнительное уравнение – условие совместности перемещений, о чем будет сказано ниже.
Выбираем основную систему. Для этого отбрасываем одну «лишнюю», с точки зрения статики связь НВ, и заменяем ее на неизвестную Х1 (рис. 3. 22, б).
2. Составляем условие совместности перемещений – каноническое уравнение метода сил:
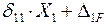= 0, (3. 39)
выражающее мысль, что перемещение точки В – точки приложения «лишней» неизвестной Х1 по ее направлению, вызванное этой неизвестной, и перемещение этой же точки и в том же направлении, вызванное внешними нагрузками, равно нулю.
3. Построение эпюр: а) Построение эпюры от единичной силы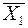 
= 1, приложенной вместо неизвестной силы Х1. Определение опорных реакций (3. 22, в):
|
|
|
; - 
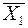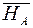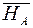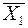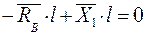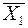= 0; = = 1;
; 
; 
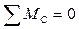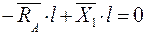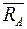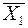= = 1.
; 
; 
= = 1.
Проверка: ; 
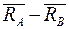= 0.
1-1 = 0.
Построение единичной эпюры: Участок АС: 
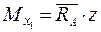; при z = 0, 
= 0; z = l; = 
.
Участок ВС: ;
=Х1 z;
z = 0, = 0; z = l, = l.
Выбираем масштаб и строим единичную эпюру (рис. 3. 22, г).
б) Построение эпюры от заданной нагрузки. Определение опорных реакций от заданных нагрузок (рис. 3. 22, д):
; 
= 0; НА = ql.
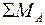= 0;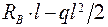 
= 0; RB = ql / 2.
; 
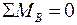= 0; RА = ql / 2.
Проверка: ; 
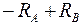= 0;
.
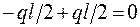Построение грузовой эпюры.
Участок ВС: ;
;
z = 0, Мх = 0; z = l, Мх = - ql2 / 2.
Участок СВ: . Приводим все силы к узлу С: равнодействующая от распределенной нагрузки ql при приведении к узлу С даст в этом узле силу ql и момент М от силы ql с плечом l/2, т. е. М = ql2 / 2. Реакция опоры В
является скользящим вектором и поэтому RB просто переместится в
точку С (рис. 3. 22, д).
Тогда имеем: Мх = 
;
z = 0, Мх = 
= –ql2 / 2;
z = l, Мх = –ql2 / 2 + ql2 / 2 = 0.
Выбираем масштаб и строим грузовую эпюру (рис. 3. 22, е).
Проверка: на концах элементов А и В значения изгибающих моментов равны нулю; в узле С моменты на обоих элементах равны друг другу, т. е. узел С должен находиться в равновесии.
4. Определяем перемещения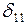 
и 
по способу Верещагина:
а) Определяем перемещение 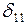перемножением единичной эпюры саму на себя (рис. 3. 22. г) с использованием ПРИЛОЖЕНИЯ 4, в котором даны формулы для вычисления w и h:
Рис. 3. 22
. (3. 40)
При этом для вычисления 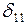и используем данные ПРИЛОЖЕНИЯ 4. Например, из подобия треугольников ВСK и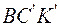 
имеем для нахождения ординаты h треугольника, у которого центр тяжести имеет координату zC = 
.
|
|
|
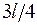Тогда имеем
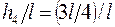; отсюда 
.
б) Определение перемещения выполняем перемножением эпюры от заданных нагрузок 
на единичную эпюру :
. (3. 41)
Определение лишней неизвестной. Подставив выражения (3. 40) и (3. 41) в (3. 39) получим:
.
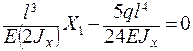Тогда: Х1 =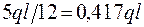 
. (3. 42)
Статическая неопределимость раскрыта.
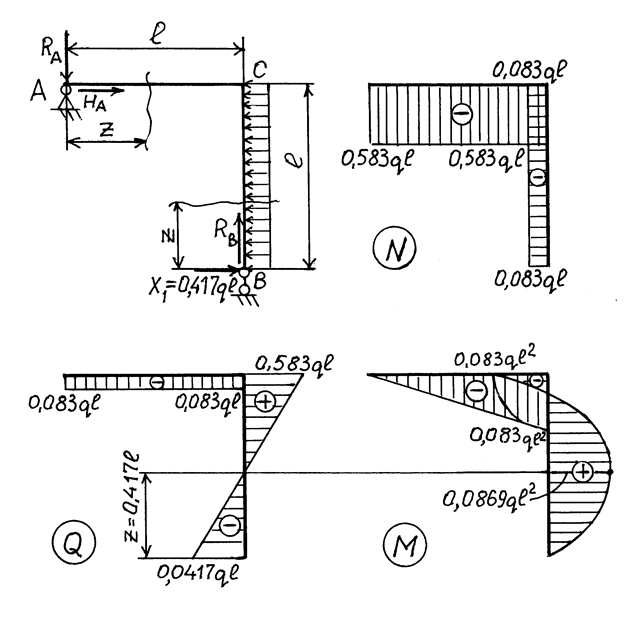
4. 5. С учетом найденного значения Х1 определяем опорные реакции и строим окончательные эпюры N, Q и М (рис. 3. 23):
; 
; НА = –Х1 + ql = –0, 417ql = 0, 583ql.
; 
; 
.
; 
; 
.
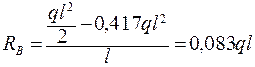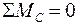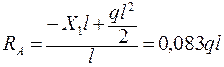Проверка: ; 
;
–0, 083 ql + 0, 083 ql = 0.
Построение эпюр N, Q и M.
Участок АС: .
N = –HA = –0, 583ql; Q = –RA = –0, 083 ql; М = –RAz,
z = 0; М = 0; z = l; М = –0, 083 ql2.
|
|
|
