 |
3.6. Расчет на прочность при прямом поперечном изгибе
|
|
|
|
(к контрольной задаче № 6)
Пример № 11. Для заданной расчетной схемы двухопорной балки (рис. 3. 11) построить эпюры поперечных сил и изгибающих моментов и подобрать стальную балку двутаврового поперечного сечения, если 
= 20 кн = 2 т, М = 20 кнм = 2 тм, q = 1, 5 кн/м = 1, 5 т/м, 
= 1 м,
= 2 м, l = 4 м,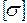 
= 160 МПа = 1600 кг/см2.
Решение: 1. Вычерчиваем балку в масштабе, наносим все нагрузки и размеры и определяем опорные реакци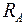и 
и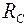 
, используя уравнение статического равновесия:
; 
;
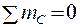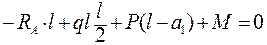= 5 т.
; 
;
= 3 т.
Проверка: 
; 
; 5 - 1, 5·4 - 2 + 3 = 0
Наносим вычисленные значения реакций RA и RC на расчетную схему.
 |
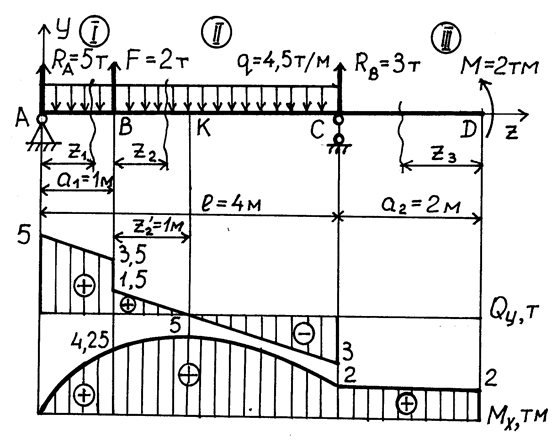Рис. 3. 11.
2. Запишем для каждого участка I, II, III балки уравнения для 
и 
и, выбрав масштаб, построим их эпюры. Для этого применим метод сечений. На каждом участке проводим произвольные сечения и выбираем начало координат: для участка I – в точке А, для Участка II – в точке В, для участка III – в точке D. Произвольные сечения каждого участка связываем с выбранным началом отсчета координат 
и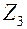 
. Тогда для каждого участка получим:
Участок I ( 
= 1 м).
; 
.
При составлении уравнения для считаем, что равнодействующая (qZ1) от равномерно распределенной нагрузки q приложена посередине рассматриваемого участка длиной Z1 и тогда плечо ее равно Z1 / 2.
При Z1 = 0; = 5 т, = 0;
При Z1 = 1 м; = 5 – 1, 5·1= 3, 5 т, = 5·1 – 5·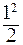 
= 4, 25 тм.
Участок II ( 
).
;
.
При составлении уравнений для и для участка II видим, что q, приложенная на участке a1, не зависит от Z2 (отсчет начинается от точки В).
При Z2 = 0; = 5 – 1, 5·1 – 2 = 1, 5 т, = 5·1 – 1, 5· 
= 4, 25 тм;
При Z2 = 3 м; = 5 – 1·2 – 1, 5·3 = –3 т,
= 5·(1 + 3) – 1, 5·1( + 3) – 2·3 – 1, 5× 
= 2 тм.
Построив эпюру для этого участка, видим, что она меняет знак с (+) на (-). Исследуем на экстремум:
|
|
|
; 
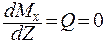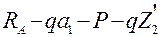
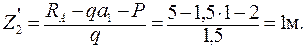
При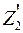 
= 1 м, = 5·(1 + 1) – 1, 5·1( + 1) – 2·1– 1, 5× 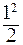= 5 тм
Откладываем от точки В 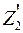= 1 м, где ( = 0), на эпюре изгибающих моментов откладываем = 5 тм и через полученные три точки проводим параболу – эпюру .
Участок III ( 
= 2 м).
= 0; = М = 2 тм.
Выбираем масштаб, строим эпюры (рис. 3. 11) и проверяем их правильность.
2. Определяем опасное сечение балки – сечение, в котором изгибающий момент принимает максимальное значение по абсолютной величине, если, как в нашем случае, материл балки пластичный.
Опасное сечение K, где 
= 5 тм.
Для подбора сечения балки из условия прочности по нормальным напряжениям при изгибе:
(3. 20)
получим формулу проектировочного расчета:
= 312, 5 см3.
По сортаменту двутавровых балок (ГОСТ 8239-89) подбираем ближайший больший профиль – двутавр № 24а с осевым моментом сопротивления 
= 317 см3.
Максимальные рабочие напряжения будут равны согласно формулы (3. 20):
кг/см2 < 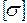= 1600 кг/см2.
Недонапряжение составит:
= –1, 44 %.
Допустимые пределы отклонения 
= ± 5 %.
Пример № 12. Для заданной расчетной схемы консольной балки (рис. 3. 12) построить эпюры поперечных сил и изгибающих моментов и подобрать деревянную балку круглого поперечного сечения, если
Р = 10 кн = 1 т, М = 20 кнм = 2 тм, q = 10 кн/м = 1 т/м, = 1, 5 м,
= 2 м, l = 3 м, 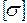= 8 МПа = 80 кг/см2.
 |
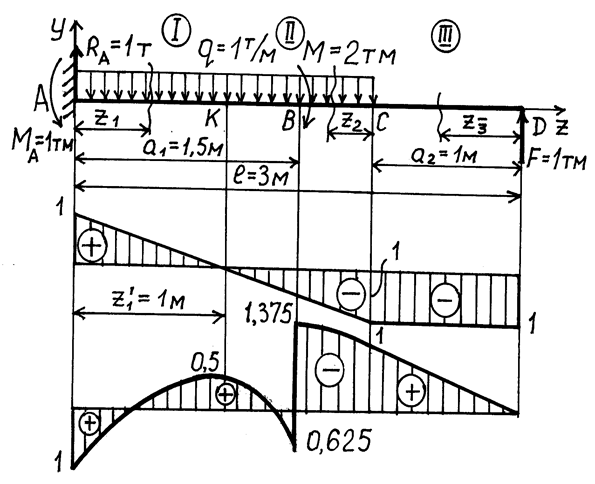Рис. 3. 12
Решение: 1. Вычерчиваем расчетную схему балки в масштабе, наносим все нагрузки и размеры. Для консольной балки можно не определять опорные реакции 
и 
, но для исключения ошибок при построении эпюр и облегчения контроля их правильности мы будем рекомендовать определять их, используя уравнения статического равновесия:
; 
;
|
|
|
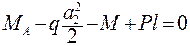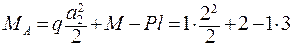= 1 тм.
; 
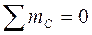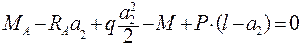
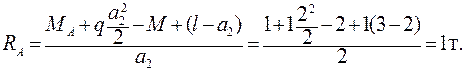
Проверка: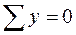 
; 
; 1 - 1·2 +1 = 0.
Наносим вычисленные значения и на чертеж.
2. Разбиваем балку на участки I, II, III, на каждом участке проводим произвольные сечения и, выбрав для каждого участка начало координат, наносим на чертеж расстояния и .
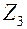Составляем для каждого участка уравнения для и и строим эпюры:
Участок I: ( = 1, 5 м).
; .
При Z1 = 0; = 1 т, = –1 тм.
При Z1 = 1, 5 м; = 1 – 1·1, 5 = 0, 5 т,
= –1 + 1·1, 5 – 1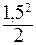 
= –0, 625 тм.
Построив эпюру , видим, что она меняет знак (+) на (-). Следовательно, на этом участке принимает экстемальное значение – максимум. Исследуем на экстремум:
; 
; 
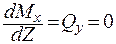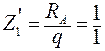= 1 м.
При 
= 1 м; = –1 + 1·1 – 1 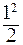= 0, 5 тм.
По полученным трем точкам строим параболу – эпюру .
Участок II ( 
0, 5 м).
;
.
При Z2 = 0; = –1 т, ; = 1(0 + (3 – 2)) = 1 тм.
При Z2 = 0, 5 м; = –1 + 1·0, 5 = –0, 5 т,
= 1(0, 5 + (3 – 2)) – 1 
= 1, 375 тм.
Участок III ( 
= 1 м).
= 1 т; 
.
При Z3 = 0; = 0.
При Z3 = 1 м; = 1× 1 = 1 тм.
3. Определяем опасное сечение и подбираем диаметр балки. Опасное сечение в точке В справа, где = 1, 375 тм.
Тогда из условия прочности (3. 20), учитывая, что осевой момент сопротивления для круглого сечения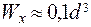 
, получим для подбора диаметра d балки формулу:
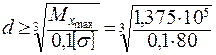= 25, 8 см.
Округляем диаметр в большую сторону до целого числа, т. е.
d = 26 см = 26·10-2 м. Тогда максимальные рабочие напряжения согласно (3. 20) будут равны
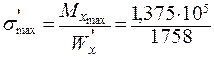= 78, 2 кг/см2 < 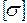= 80 кг/см2.
где = 0, 1·263= 1758 см3.
Недонапряжение составит
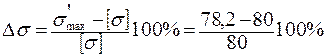= –2, 25 % < ±5 %.
Расчет окончен.
|
|
|
