 |
Задача 11. таблица 2. 9. 2. Частоту изменения возмущающей силы ;. 3. Коэффициент нарастания колебаний. 3. Примеры решения задач по темам
|
|
|
|
ЗАДАЧА 11
На двух балках двутаврового сечения установлен двигатель весом 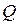 (рис. 2. 10), делающий
(рис. 2. 10), делающий  оборотов в минуту. Центробежная сила инерции, возникающая вследствие неуравновешенности вращающихся частей двигателя, равна
оборотов в минуту. Центробежная сила инерции, возникающая вследствие неуравновешенности вращающихся частей двигателя, равна  . Собственный вес балок и силы сопротивления можно не учитывать. Требуется найти:
. Собственный вес балок и силы сопротивления можно не учитывать. Требуется найти:
1. Частоту собственных колебаний  ;
;
2. Частоту изменения возмущающей силы  ;
;
3. Коэффициент нарастания колебаний

(если коэффициент  , определимый по формуле, окажется отрицательным, то в дальнейшем расчете следует учитывать его абсолютную величину);
, определимый по формуле, окажется отрицательным, то в дальнейшем расчете следует учитывать его абсолютную величину);
4. Динамический коэффициент
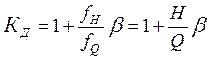 ;
;
5. Наибольшее нормальное напряжение в балках
 .
.
Данные взять из табл. 2. 9.
Таблица 2. 9
| № строки | Схема по рис. 2. 10 | № двутавра |  , м , м
| 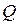 , кН , кН
|  , кН , кН
|  ,
об/мин ,
об/мин
|
| I II III IV V VI VII VIII IX X | 20а 22а 24а 27а | 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | ||||
| в | б | в | а | б | в |
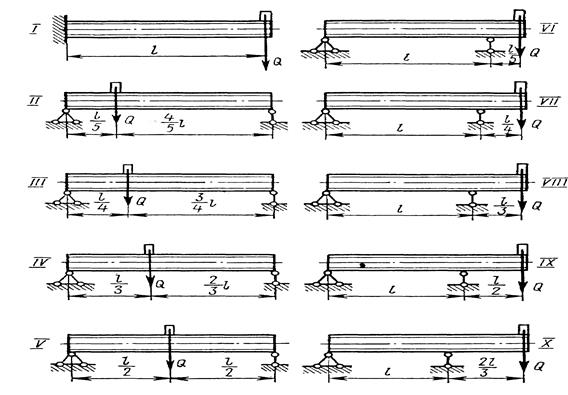
Рис. 2. 10
ЗАДАЧА 12
В опасном сечении вала с диаметром  действует крутящий момент Т и изгибающий момент
действует крутящий момент Т и изгибающий момент  . Вал сделан из улеродистой стали (предел прочности которой равен
. Вал сделан из улеродистой стали (предел прочности которой равен  , а предел текучести
, а предел текучести  ) и не имеет резких переходов, выточек, канавок; поверхность его чисто обработана резцом.
) и не имеет резких переходов, выточек, канавок; поверхность его чисто обработана резцом.
Определить коэффициент запаса прочности в опасном сечении вала, приняв нормальные напряжения изгиба изменяющимся по симметричному циклу, а касательные напряжения кручения – по пульсирующему циклу (от нуля до максимального значения).
|
|
|
Коэффициенты напряжений и масштабные коэффициенты можно считать, соответственно, одинаковыми для нормальных и для касательных напряжений.
Данные взять из табл. 2. 10.
Таблица 2. 10
| № строки |
| Т | 
| sВ | sТ |
| Н·м | Н·м | МПа | МПа | ||
| в | б | в | б | б |
Порядок выполнения решения: 1) Найти максимальные нормальные напряжения и максимальные касательные напряжения; 2) по эмпирическим формулам найти предел текучести при кручении и пределы выносливости при кручении и изгибе; 3) найти действительный коэффициент концентрации напряжений по формуле
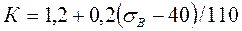 .
.
4) найти масштабный коэффициент по формуле:
 ,
,
где  - в сантиметрах;
- в сантиметрах;
5) найти коэффициенты запаса прочности по нормальным и касательным напряжениям;
6) найти общие коэффициенты запаса прочности по усталому разрушению и текучести.
3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ТЕМАМ
КОНТРОЛЬНЫХ РАБОТ
Контрольные работы выполняются по основным темам курса. В рассматриваемом разделе представлены примеры решения задач, позволяющие после их проработки самостоятельно решить контрольные задачи.
3. 1. Статически определимые задачи на растяжение и сжатие
(к контрольной задаче № 1)
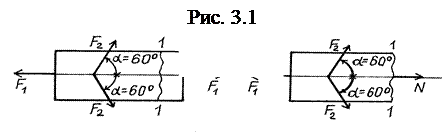
Пример № 1. Определить величину продольной силы в сечении I – I бруса, находящегося в равновесии, если  = 20 кН = 2·103 кг,
= 20 кН = 2·103 кг,
 = 10 кН = 1·103 кг,
= 10 кН = 1·103 кг,  = 10 кН = 1·103 кг,
= 10 кН = 1·103 кг,  = 60º (рис. 3. 1).
= 60º (рис. 3. 1).
Решение: Пользуясь методом сечений:
а) рассекаем брус по заданному сечению;
б) отбрасываем любую, например, правую часть бруса (рис. 3. 1, б);
в) заменяем ее действие на оставшуюся часть неизвестной продольной силой N, направив ее от сечения, т. е. предполагая, что продольная сила – растягивающая;
|
|
|
г) составляем условие статического равновесия и вычисляем N:
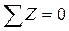 ;
;  ;
;
 = 1× 103 кг = 10 кН,
= 1× 103 кг = 10 кН,
т. е. 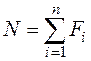 . (3. 1)
. (3. 1)
Таким образом, продольная сила в поперечном сечении бруса численно равна алгебраической сумме проекций на его ось всех внешних сил, приложенных по одну сторону от сечения.
Пример № 2. Построить эпюру продольных сил и вычислить диаметр стального короткого бруса, если  = 40 кН = 4·103 кг,
= 40 кН = 4·103 кг,  =
=
30 кН = 3·103 кг,  = 80 кН = 8·103 кг; допускаемое напряжение на растяжение и сжатие принять
= 80 кН = 8·103 кг; допускаемое напряжение на растяжение и сжатие принять  = 160 МПа = 1600 кг/см2 (рис. 3. 2).
= 160 МПа = 1600 кг/см2 (рис. 3. 2).
Решение: 1. Используя формулу (3. 1) из предыдущей задачи, для каждого из 3-х участков получим (рис. 3. 2, а):
сечение 1 – 1  = –4000 кг = –40 кН,
= –4000 кг = –40 кН,
сечение 2 – 2  = –4000 + 3000 = –1000 кг = –10 кН,
= –4000 + 3000 = –1000 кг = –10 кН,
 сечение 3 – 3
сечение 3 – 3  =–4000 + 3000 + 8000=7000кг = 70кН.
=–4000 + 3000 + 8000=7000кг = 70кН.
2. Проводим рядом с брусом ось, параллельную его продольной оси, и, выбрав масштаб, откладываем по длине каждого участка найденные значения продольных сил  ,
, 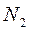 и
и 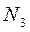 , т. е. строим эпюру N (рис. 3. 2, б).
, т. е. строим эпюру N (рис. 3. 2, б).
3. Определяем опасное сечение – сечение, в котором нормальные напряжения максимальны (для пластичных материалов берем по абсолютной величине), т. е.
|

где А – площадь поперечного
сечения бруса.
В нашем случае для всех трех участков площадь поперечного сечения А постоянна и по абсолютной величине  >
>  >
> 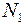 . Опасное сечение – любое сечение участка 3, где
. Опасное сечение – любое сечение участка 3, где  = 7000кг = 70кН. Тогда из условия прочности на растяжение и сжатие для расчета площади поперечного сечения применим формулу проектировочного расчета:
= 7000кг = 70кН. Тогда из условия прочности на растяжение и сжатие для расчета площади поперечного сечения применим формулу проектировочного расчета:
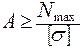 ;
; 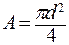 .
.
Отсюда
 = 2, 36 см = 2, 36·10-2 м.
= 2, 36 см = 2, 36·10-2 м.
Пример № 3. Для стального ступенчатого бруса (Е = 2·105МПа = 2·106 кг/см2), нагруженного осевыми внешними силами  = 150 кН = 15·103 кг,
= 150 кН = 15·103 кг,  = 100 кН = 10·103 кг, при длине участков
= 100 кН = 10·103 кг, при длине участков 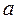 = 30 cм, b = 20 см,
= 30 cм, b = 20 см, 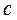 = 15 см и площади поперечного сечения A = 10 см2 требуется: 1. Определить внутренние продольные силы
= 15 см и площади поперечного сечения A = 10 см2 требуется: 1. Определить внутренние продольные силы 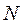 и построить их эпюру. 2. Вычислить для каждого участка напряжения
и построить их эпюру. 2. Вычислить для каждого участка напряжения  и построить их эпюру. 3. Выполнить полную абсолютную деформацию бруса и определить перемещение сечения I – I. (рис. 3. 3).
и построить их эпюру. 3. Выполнить полную абсолютную деформацию бруса и определить перемещение сечения I – I. (рис. 3. 3).
|
|
|
 |
а) б) в)
Рис. 3. 3
1. Определяем внутренние продольные силы. Имеем два силовых участка длиной (а + b) и c. Для первого участка, согласно (3. 1) имеем
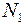 =
=  = 15·103 кг = 150 кН (растяжение);
= 15·103 кг = 150 кН (растяжение);
для второго участка:
 =
=  –
–  = 15·103 – 20·103 = –5·10-3 кг = –50 кН (сжатие).
= 15·103 – 20·103 = –5·10-3 кг = –50 кН (сжатие).
Выбираем масштаб и строим эпюру  (рис. 3. 3, б).
(рис. 3. 3, б).
2. Вычисление нормальных напряжений выполняем по формуле согласно раздела 2. 2.
На участках а и b площадь поперечного сечения одинакова и равна 2А=20 см2. Тогда
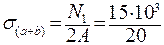 = 750 кг/см2 = 75 МПа;
= 750 кг/см2 = 75 МПа;
на участке  :
:
 = –500 кг/см2 = –50 МПа.
= –500 кг/см2 = –50 МПа.
Выбираем масштаб и строим эпюру  (рис. 3. 3, в).
(рис. 3. 3, в).
3. Полная деформация бруса:
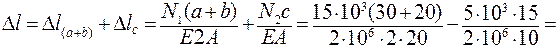
= 0, 00973 – 0, 00375 = 0, 00562 см = 0, 0562× 10-3 м.
3. Поскольку верхнее сечение защемлено, то перемещение заданного сечения I – I численно будет равно абсолютной деформации участков бруса b и c, т. е.
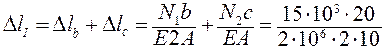 – 0, 00375 = 0, 00375 см = 0, 0375× 10-3 м.
– 0, 00375 = 0, 00375 см = 0, 0375× 10-3 м.
|
|
|


