 |
3.5. Геометрические характеристики сечений
|
|
|
|
(к контрольной задаче №5)
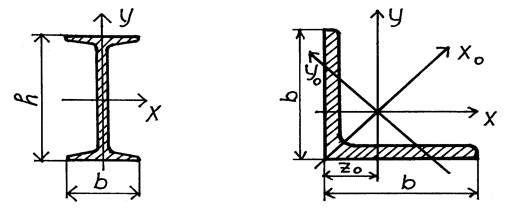
Пример № 9. Для поперечного сечения (рис. 3. 9), состоящего из двутавра №10 и равнобокого уголка 50х50х5 мм, требуется: 1) определить положение центра тяжести сечения; 2) найти центральные осевые и центробежный моменты инерции сечения; 3) определить направление главных центральных осей инерции сечения ( 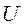 и
и  ); 4) вычислить главные центральные моменты инерции сечения.
); 4) вычислить главные центральные моменты инерции сечения.
Решение: выписываем из таблиц сортамента прокатных профилей (см. ПРИЛОЖЕНИЯ 1 и 2)необходимые для расчета данные:
а) Двутавр №10 (ГОСТ 8239-56) Уголок равнобокий 50х50х5
(ГОСТ 8509-57)
 |




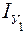
| F =12 см2 А2
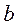 = 5, 5 см b2 = 5, 5 см b2
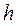 = 10 см = 10 см 
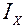 = 198 см4 = 198 см4 
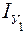 = 17, 9 см4 = 17, 9 см4
| A = 4, 8 см2
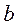 = 5 см = 5 см
 = 1, 42 см = 1, 42 см
 = 11, 2см4 = 11, 2см4
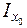 = 17, 8 см4 = 17, 8 см4
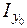 = 4, 63 см4 = 4, 63 см4
|
Примечание: Слева от вертикальной черты для каждого профиля проставляем при решении задачи обозначения геометрических параметров, принятые нами в соответствии с чертежом (рис. 3. 9).
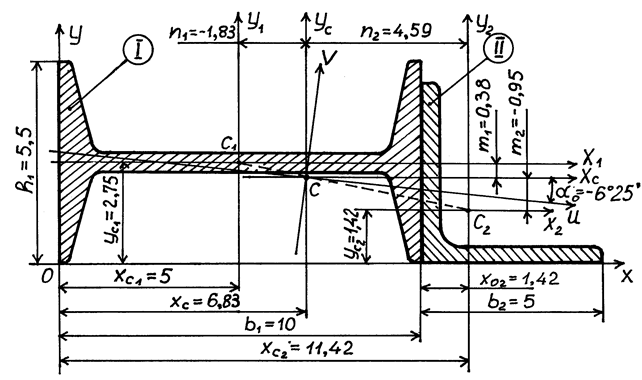
Рис. 3. 9
1. Вычерчиваем в масштабе сечение. Для определения положения центра тяжести составного сечения обозначим двутавр – I и равнобокий уголок – II и проводим собственные центральные оси  и
и  . Проводим вспомогательные оси
. Проводим вспомогательные оси  . Тогда координаты центра тяжести сечений I и II относительно осей
. Тогда координаты центра тяжести сечений I и II относительно осей  :
:
 = 5 см;
= 5 см;  = 2, 75 см;
= 2, 75 см;
 = 10 + 1, 42 = 1, 14 см;
= 10 + 1, 42 = 1, 14 см;  = 1, 42 см.
= 1, 42 см.
Координаты центра тяжести всего сечения
 = 6, 83 см;
= 6, 83 см;
 = 2, 37 см.
= 2, 37 см.
где А1 = 12 см2; А2 = 4, 8 см2 – площади поперечных сечений.
Наносим эти размеры на чертеж и через полученный центр тяжести С проводим центральные оси 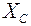 и
и 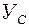 . Проверяем правильность вычислений: центр тяжести составного сечения должен лежать на линии, соединяющей центры тяжести первого и второго сечений.
. Проверяем правильность вычислений: центр тяжести составного сечения должен лежать на линии, соединяющей центры тяжести первого и второго сечений.
|
|
|
2. Вычисляем центральные осевые и центробежный моменты инерции составного сечения. Воспользуемся формулами для определения моментов инерции при параллельном переносе осей:
 ;
; 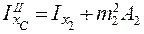 ;
;
 ;
; 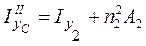 ; (3. 16)
; (3. 16)
 ;
;  .
.
где  ,
, 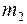 – расстояние между параллельными осями
– расстояние между параллельными осями 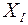 и ХС,
и ХС,  и ХС, соответственно;
и ХС, соответственно;
n1, n2 – расстояние между параллельными осями  и
и 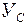 ,
,  и
и 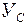 , соответственно.
, соответственно.
На основании данных чертежа получим:
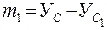 = 2, 75 – 2, 37 = 0, 38 см;
= 2, 75 – 2, 37 = 0, 38 см;
 = –(2, 27 – 1, 42) = –0, 95 см;
= –(2, 27 – 1, 42) = –0, 95 см;
 = –(6, 83 – 5) = –1, 83 см;
= –(6, 83 – 5) = –1, 83 см;
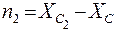 = 11, 42 – 6, 83 = 4, 59 см.
= 11, 42 – 6, 83 = 4, 59 см.
Вычисляем центральные осевые моменты инерции всего сечения, равные сумме моментов инерции, фигур составляющих это сечение, с учетом формулы (3. 16):
 = (17, 9 +0, 382× 12) +
= (17, 9 +0, 382× 12) +
+ (11, 2 + (– 0, 95)2× 4, 8) = 19, 63 + 15, 53 = 352 см4; (3. 17)
 = (198 + (– 1, 83)2× 12) +
= (198 + (– 1, 83)2× 12) +
+(11, 2 + 4, 592× 4, 8) = 238, 2 + 111, 9 = 350, 1 см4. (3. 18)
Центробежный момент инерции составного сечения вычисляем с учетом формул (3. 16) аналогично:
 =
=
= (0 + 0, 38× (– 1, 83)× 12) + (– 6, 58 + (– 0, 95)× 4, 59× 4, 8) = (– 8, 34) + (– 27, 5) = – 35, 8 см4. (3. 19)
В этой формуле для двутавра, являющегося симметричным сечением относительно собственных центральных осей, центробежный момент инерции 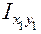 = 0, т. к. эти оси главные центральные оси двутавра. Для равнобокого уголка (
= 0, т. к. эти оси главные центральные оси двутавра. Для равнобокого уголка ( 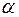 = 45º ):
= 45º ):
 ;
;  = –6, 58 см4.
= –6, 58 см4.
 Рис. 3. 10
Рис. 3. 10
| Знак  при различных положениях равнобоких и неравнобоких уголков выбирается согласно рис. 3. В нашем случае берется знак минус.
3. Определим направ-
авление главных централь-
альных осей на основании вычислений по формулам (3. 17), (3. 18) и (3. 19): при различных положениях равнобоких и неравнобоких уголков выбирается согласно рис. 3. В нашем случае берется знак минус.
3. Определим направ-
авление главных централь-
альных осей на основании вычислений по формулам (3. 17), (3. 18) и (3. 19):
|
 = –0, 2274;
= –0, 2274;
2  = –12º 48’;
= –12º 48’;  = –6º 24’.
= –6º 24’.
Угол  < 0, поэтому угол
< 0, поэтому угол  = –6º 24’ отложим от оси ХС в направлении часовой стрелки и проведем главную ось
= –6º 24’ отложим от оси ХС в направлении часовой стрелки и проведем главную ось 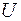 , а ей перпендикулярно – главную ось
, а ей перпендикулярно – главную ось 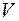 (рис. 3. 9).
(рис. 3. 9).
|
|
|
4. Вычислим значения главных центральных моментов инерции

 = 354 см4 = 354·10-8 м4;
= 354 см4 = 354·10-8 м4;
 = 31, 2 см4 = 31, 2·10-8 м4.
= 31, 2 см4 = 31, 2·10-8 м4.
Положение оси U (  ) легко определить, т. к. эта ось, во-первых, пересекает сечение по наибольшему протяжению и, во-вторых располагается ближе к той центральной оси инерции (оси ХС), относительно которой центральный момент инерции имеет меньшую величину, т. е. (
) легко определить, т. к. эта ось, во-первых, пересекает сечение по наибольшему протяжению и, во-вторых располагается ближе к той центральной оси инерции (оси ХС), относительно которой центральный момент инерции имеет меньшую величину, т. е. ( 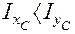 ).
).
Таким образом  = 31, 2·10-8 м4,
= 31, 2·10-8 м4,
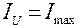 = 354 см4 = 354·10-8 м4.
= 354 см4 = 354·10-8 м4.
Проверка: а) 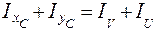 ;
;
 см4;
см4;
 см4.
см4.
б) Т. к. оси 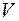 и
и 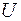 главные, то должно выполняться условие равенства нулю центробежного момента инерции, вычисленного относительно главных осей
главные, то должно выполняться условие равенства нулю центробежного момента инерции, вычисленного относительно главных осей 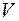 и
и 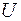 , т. е.
, т. е.  = 0. Тогда при
= 0. Тогда при  = –6º 25’ получим:
= –6º 25’ получим:
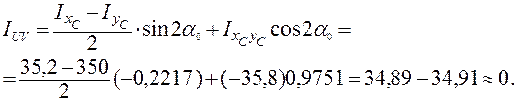
где  ,
,
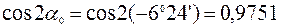 .
.
|
|
|


