 |
Абстрактное описание процесса
|
|
|
|
ФУНКЦИОНИРОВАНИЯ ОБЪЕКТОВ
Если отойти от конкретного содержания процесса функционирования технического объекта, то в простейшем случае может быть предложена его математическая модель. В любой произвольный процесс времени t объект может находиться в одном из двух состояний:
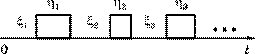
Рис.1.3
Процесс функционирования объекта
отказа или работоспособности. Обозначим неизвестное текущее состояние объекта в момент времени t через Z(t), состояние отказа через  и состояние работоспособности через Z. Весь процесс функционирования объекта можно представить чередующейся последовательностью случайных величин
и состояние работоспособности через Z. Весь процесс функционирования объекта можно представить чередующейся последовательностью случайных величин  (рис. 1.3), где
(рис. 1.3), где  — длительность i -го по счету
— длительность i -го по счету
периода работоспособности, а  — длительность периода отказа. Все введенные символы взаимосвязаны следующими соотношениями:
— длительность периода отказа. Все введенные символы взаимосвязаны следующими соотношениями:
 (1. 1)
(1. 1)
Рассмотрим теперь систему, состоящую из n элементов. Состояние системы в момент времени t определяется состоянием отдельных ее элементов в этот момент. Если состояние j -го элемента системы в момент времени t обозначить через  (t), то состояние системы можно записать в виде
(t), то состояние системы можно записать в виде
 (1. 2)
(1. 2)
Определенным совокупностям состояний элементов соответствует состояние исправности системы в целом Z (например, состояние  всегда есть состояние исправности для системы). Другим совокупностям состояний элементов соответствует состояние отказа системы в целом
всегда есть состояние исправности для системы). Другим совокупностям состояний элементов соответствует состояние отказа системы в целом  .
.
| Рис. 1.4 Схема перехода из одного состояния в другое |
Поясним сказанное на примере системы из двух элементов. Всего возможно четыре различных состояния системы, определяемых состояниями отдельных элементов:
| Рис. 1.5 Последовательное соединение элементов в системе |
 (1.3)
(1.3)
 С течением времени система может переходить из одного состояния в другое (рис. 1.4).
С течением времени система может переходить из одного состояния в другое (рис. 1.4).
|
|
|
 Рассмотрим структуру последовательного соединения элементов в системе, т. е. такое соединение, в котором отказ хотя бы одного элемента приводит к отказу всей системы (рис. 1.5). В этом случае Z1 = Z, а совокупность состояний
Рассмотрим структуру последовательного соединения элементов в системе, т. е. такое соединение, в котором отказ хотя бы одного элемента приводит к отказу всей системы (рис. 1.5). В этом случае Z1 = Z, а совокупность состояний  составит состояние отказа системы
составит состояние отказа системы  .
.
| Рис. 1.6 Параллельное соединение элементов в системе |
Для другой характерной структуры — параллельного соединения элементов (рис. 1.6) — отказ наступает лишь при одновременном отказе всех элементов  а остальные состояния
а остальные состояния  представляют собой состояние работоспособности системы Z.
представляют собой состояние работоспособности системы Z.
| Рис. 1.7 Пространство состояний системы |

 Все множество состояний системы принято называть фазовым пространством состояний системы. В общем случае фазовое пространство не обязательно является дискретным. Рассмотрим в качестве примера систему из таких элементов, когда хотя бы один из них характеризуется непрерывным множеством состояний. Это может произойти, если основной рабочий параметр принимает любые значения из некоторого интервала. Пусть j -й элемент характеризуется некоторым значением параметра Y(t) в момент времени t, которое и определяет полностью его состояние в указанный момент времени. Тогда состояние системы, состоящей из n таких элементов, будет в момент времени описываться вектором из n -мерного непрерывного пространства
Все множество состояний системы принято называть фазовым пространством состояний системы. В общем случае фазовое пространство не обязательно является дискретным. Рассмотрим в качестве примера систему из таких элементов, когда хотя бы один из них характеризуется непрерывным множеством состояний. Это может произойти, если основной рабочий параметр принимает любые значения из некоторого интервала. Пусть j -й элемент характеризуется некоторым значением параметра Y(t) в момент времени t, которое и определяет полностью его состояние в указанный момент времени. Тогда состояние системы, состоящей из n таких элементов, будет в момент времени описываться вектором из n -мерного непрерывного пространства
 (1. 4)
(1. 4)
Простейший случай для системы из двух элементов пространства состояний показан на рис. 1.7. Пусть  — область допустимых значений, соответствующих работоспособности системы. Выход из этой области во внешнюю область определяет состояние отказа. Здесь изображено блуждание системы в процессе функционирования из состояния Уо в состояние отказа Y\, откуда за счет некоторых восстановительных мероприятий (например, регулировки или замены элементов) система переведена в работоспособное состояние. Вне зависимости от того, рассматриваем мы дискретное или непрерывное фазовое пространство при исследовании надежности, всегда остается одна существенная сторона этого фазового пространства: она четко подразделяется на состояние двух типов — работоспособности и отказа.
— область допустимых значений, соответствующих работоспособности системы. Выход из этой области во внешнюю область определяет состояние отказа. Здесь изображено блуждание системы в процессе функционирования из состояния Уо в состояние отказа Y\, откуда за счет некоторых восстановительных мероприятий (например, регулировки или замены элементов) система переведена в работоспособное состояние. Вне зависимости от того, рассматриваем мы дискретное или непрерывное фазовое пространство при исследовании надежности, всегда остается одна существенная сторона этого фазового пространства: она четко подразделяется на состояние двух типов — работоспособности и отказа.
|
|
|
1.3.
|
|
|


