Единичные показатели надежности объектов

 

Свойство надежности	Единичный показатель надежности
Безотказность	Вероятность безотказной работы. Средняя наработка до отка­за. Гамма-процентная наработка до отказа. Средняя нара­ботка на отказ. Интенсивность отказов. Параметр потока отказов
Долговечность	Средний ресурс. Гамма-процентный ресурс. Назначенный ресурс. Средний срок службы. Гамма-процентный срок служ­бы. Назначенный срок службы
Ремонтопри­годность	Вероятность восстановления в заданное время. Среднее вре­мя восстановления. Интенсивность восстановления
Сохраняемость	Средний срок сохраняемости. Гамма-процентный срок сохра­няемости

работы, то ВБР записывается в виде

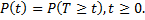
Случайная величина Т являет­ся неотрицательной и имеет дис­кретное или непрерывное распреде­ление. Функция ВБР наиболее пол­но определяет надежность объекта и обладает следующими очевидны­ми свойствами:

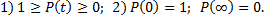(1. 5)

График функции показан на рис. 1. 9.

Статистически ВБР составляет

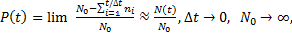(1. 6)

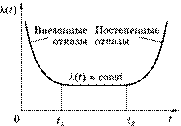
где 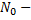число объектов в начале испытаний; 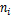— число отказав­ших объектов в интервале времени 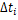; t — время, для которого определяется ВБР; N(t) — число объектов, исправно работающих на интервале [0, t ].

Вероятность того, что отказ объекта произойдет за время, не превышающее заданной величины t, т. е. что Т < t, как вероятность события, противоположного тому, при котором , составляет

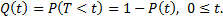(1. 7)

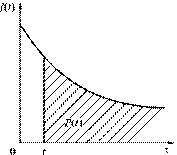
Функция Q(t) есть интегральная функция распределения слу­чайной величины, т. е. Q(t) = F(t). Если функция Q(t) дифферен­цируема, то производная от интегральной функции распределе­ния есть дифференциальный закон (плотность) распределения слу­чайной величины Т — времени исправной работы:

(1. 8)

Таким образом, безотказность объекта также можно характе­ризовать плотностью вероятностей момента первого отказа. Ста­тистически вероятность отказа:

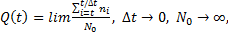(1. 9)

где 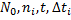, имеют те же значения, что и в выражении (1.6).

График функции f(t) показан на рис. 1.10. Плотность вероят­ности f(t) статистически определяется по формуле

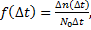(1. 10)

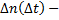где число отказов за интервал времени Очевидно, что

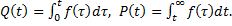(1. 11)

В качестве меры показателей на­дежности используются: наработка на отказ 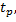время восстановления 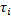средний ресурс — средняя наработ­ка до предельного состояния; средняя интенсивность отказов λ и среднее значение параметра пото­ка отказов и т. д. Эти показатели измеряются в часах, долях года или в годах, показывая продолжительность или объем работы ЭА.

Средняя наработка до отказа 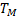(среднее время безотказной работы) является математическим ожиданием времени безотказ­ной работы. Наработка на отказ t_P (среднее время между сосед­ними отказами) — среднее значение наработки ремонтируемого изделия между отказами. Интенсивность отказов λ — вероят­ность отказов неремонтируемого изделия в единицу времени при условии, что до этого момента отказа объекта не возникало.

Некоторые показатели надежности являются нормируемыми, значения которых устанавливаются нормативно-технической до­кументацией, например, нормированный или утяжеленный режим работы, износостойкость коммутационных ЭА. Утяжеленный ре­жим — рабочее состояние ЭА, при котором независимо от режима работы не обеспечивается резервирование установленных пределов.

Средняя наработка до отказа. Функции распределения (инте­гральная функция или плотность) полностью характеризуют слу­чайную величину. Однако для решения некоторых задач доста­точно знать только несколько моментов случайной величины. На­помним, что моментом - г o порядка называют интеграл

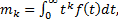(1. 12)

если величина этого интеграла конечна.

В теории надежности чаще всего используют моменты первых двух порядков. Момент первого порядка (математическое ожида­ние) наработки до первого отказа обозначают 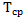и называ­ют средней наработкой до отказа (или средним временем безотказ­ной работы):

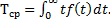(1. 13)

Статистическая средняя наработка до отказа однотипных объектов составляет

(1. 14)

где 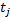— время исправной работы -го объекта.

Гамма-процентная наработка до отказа — это наработка, в течение которой отказ объекта не возникнет с вероятностью 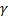, выраженной в процентах. Она определяется из уравнения

(1. 15)

При 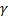= 100% гамма-процентная наработка называется уста­новленной безотказной наработкой, при 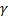= 50% — медианной.

Средняя наработка на отказ — это отношение наработки вос­станавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки:

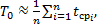(1. 16)

где 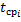— время исправной работы между 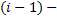м и ί - м отказами объекта; n — число отказов объекта.

При достаточно большом числе отказов будет стремиться к среднему времени между двумя соседними отказами. Если испы­тания проводятся не с одним, а с несколькими однотипными объ­ектами, то среднее время между отказами можно определить из выражения

(1. 17)

где M – число объектов.

Интенсивность отказов — это отношение числа отказавших объектов в единицу времени к среднему числу объектов, продол­жающих исправно работать в данный интервал времени:

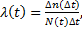(1. 18)

где An(At) — число отказов объекта за промежуток времени от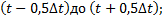

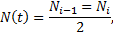
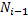— число исправно работающих объектов в начале интервала

време­ни ; , — число исправно рабо­тающих объектов в конце

интерва­ла времени .

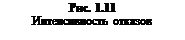Интенсивность отказов часто на­зывают λ-характеристикой, она по­казывает, какая часть объектов вы­ходит из строя в единицу времени по отношению к среднему числу исправно работающих объектов. Характерная кривая интенсивности отказов объектов показана на рис. 1.11, из которого видно, что кривая изменения интенсивности отказов имеет три участка: приработка (0 - 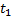), нормальная эксплуа­тация ( 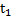- 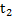),интенсивный износ и старение 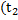и далее).

В период приработки выявляются отказы по вине проектиров­щиков, конструкторов и изготовителей — как правило, внезап­ные. Период нормальной эксплуатации характеризуется наимень­шим количеством отказов иприблизительным постоянством ин­тенсивности отказов 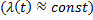. Третий период обусловлен таким значением износа и старения объекта, что его дальнейшая эксплуа­тация нецелесообразна.

Параметр потока отказов — это отношение среднего числа от­казов восстанавливаемого объекта за произвольно малую его на­работку к значению этой наработки. Параметр потока отказов используют в качестве показателя безотказности восстанавливае­мых объектов, эксплуатация которых может быть описана сле­дующим образом: в начальный момент времени объект начинает работу и работает до отказа; после отказа происходит восстанов­ление работоспособности, и объект вновь работает до отказа и т. д. При этом время восстановления не учитывается: принимается, что восстановление работоспособности происходит как бы мгновенно.

Для таких объектов моменты отказов на оси суммарной наработ­ки или на оси непрерывного времени образуют поток отказов. В качестве характеристики потока отказов используют «ведущую функцию» данного потока — математическое ожидание чис­ла отказов за время t:

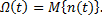(1. 19)

Параметр потока отказов 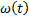характеризует среднее число от­казов, ожидаемых на малом интервале времени:

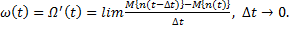(1. 20)

Параметр потока отказов связан с ведущей функцией соотно­шением

Статистически параметр потока отказов можно определить по формуле

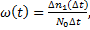(1.21)

где 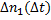— общее число отказов восстанавливаемого объекта за интервал времени от

.

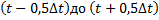Простейший поток однородных отказов обладает тремя свой­ствами: стационарностью, отсутствием последствий и ординарно­стью. Стационарность процесса заключается втом, что события зависят не от начала интервала , а от рассматриваемого интер­вала . Отсутствие последствия означает, что событие не зависит от событий, происходящих до начала интервала. 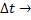Ординарность потока означает, что вероятность возникновения двух или более событий за интервал стремится к нулю при 0:

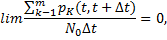
Таким образом, за короткий интервал времени возникновение двух событий практически невозможно.

Средний ресурс 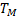— это математическое ожидание ресурса.

Гамма-процентный ресурс — это наработка, в течение ко­торой объект не достигнет предельного состояния с заданной ве­роятностью 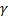, выраженной в процентах. Гамма-процентный ресурс определяется по формуле (1.15).

Назначенный ресурс 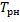определяется как суммарная наработ­ка объекта, при достижении которой применение по назначению должно быть прекращено.

Средний срок службы 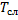— это математическое ожидание срока­ службы.

Гамма-процентный срок службы характеризуется кален­дарной продолжительностью от начала эксплуатации объекта, в течение которой он не достигнет предельного состояния с задан­ной вероятностью 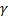, выраженной в процентах (см. (1. 15)).

Назначенный срок службы это календарная продол­жительность эксплуатации объекта, при достижении которой при­менение по назначению должно быть прекращено.

Назначенный ресурс (срок службы) —- это показатель надеж­ности, устанавливаемый на основании субъективных или органи­зационных принципов, являющихся поэтому косвенными пока­зателями надежности.

Момент восстановления работоспособности объекта после от­каза является случайным событием. Поэтому интервал времени от момента отказа до момента восстановления является случай­ной величиной, и для характеристики ремонтопригодности может быть использована функция распределения этой случайной вели­чины θ. Вероятностью восстановления называется вероятность того, что время восстановления работоспособного состояния объ­екта не превысит заданного:

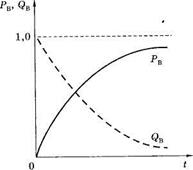
(1.22)

Функция представляет собой интегральную функцию рас­пределения случайной величины θ. Вероятность невосстановления на заданном интервале t, т. е. веро­ятность того, что , составит

(1.23)

Вероятности и по­казаны на рис. 1.12.

Рис. 1.12 Кривые вероятности восстановления и невосстановления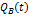

Плотность вероятности момен­та восстановления:

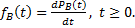(1.24)

 

По аналогии со средней наработкой до отказа момент первого порядка (математическое ожидание) времени восстановле­ния работоспособного состояния объекта называется средним вре­менем восстановления:

(1.25)

Так как

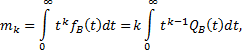
то

(1.26)

Статистически среднее время восстановления составляет

(1.27)

где 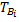— время обнаружения и устранения ί - гo отказа объекта.

Время, затрачиваемое на обнаружение и устранение отказов, зависит от ряда факторов: конструкции объекта, квалификации обслуживающего персонала, наличия специальных контрольных режимов, встроенных контрольных устройств, качества испыта­тельных тестов, сигнализации и др.

Важным показателем ремонтопригодности объекта является интенсивность восстановления которая, следуя общей методологии, аналогична показателю «безотказности» — интенсивно­сти отказов.

Показатели сохраняемости — средний срок сохраняемости и гамма-процентный срок сохраняемости — определяются аналогич­но соответствующим показателям безотказности и долговечности. Средний срок сохраняемости — это математическое ожидание сро­ка сохраняемости, а гамма-процентный срок сохраняемости — это срок сохраняемости, достигаемый объектом с заданной вероятно­стью 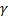, выраженной в процентах.

 

1.5.

КОМПЛЕКСНЫЕ ПОКАЗАТЕЛИ

НАДЁЖНОСТИ ОБЪЕКТОВ

Вероятностные характеристики отдельных свойств надежно­сти в общем случае являются независимыми. Один объект может обладать высокими показателями безотказности, но быть плохо ремонтопригодным. Другой объект может быть долговечным, но обладать низкими показателями безотказности. Конечно, жела­тельно иметь объекты, обладающие хорошими показателями и безотказности, идолговечности, и ремонтопригодности, но осу­ществить это не всегда удается. Для оценки нескольких свойств надежности используются комплексные показатели.

Коэффициент готовности — это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых при­менение объекта по назначению не предусматривается:

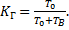(1.28)

Коэффициент оперативной готовности определяется как ве­роятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусмат­ривается, и начиная с этого момента будет работать безотказно в течение заданного интервала времени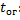

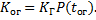(1.29)

Коэффициент оперативной готовности характеризует надеж­ность объектов, необходимость применения которых возникает в произвольный момент времени, после которого требуется опреде­ленная безотказная работа. До этого момента времени такие объек­ты могут находиться как в режиме дежурства (при полных или об­легченных нагрузках, но без выполнения заданных рабочих функ­ций), так и в режиме применения для выполнения других рабочих функций (задач, работ и т. д.). В обоих режимах возможно возник­новение отказов и восстановление работоспособности объекта. Иногда пользуются коэффициентом простоя:

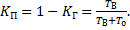(1.30)

Коэффициент технического использования — это отношение математического ожидания интервалов времени пребывания объ­екта в состояниях простоев, обусловленных техническим обслу­живанием и ремонтами, за тот же период эксплуатации:

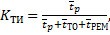(1.31)

где — математическое ожидание наработки восстанавливаемо­го объекта; 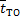— математическое ожидание интервалов времени простоя при техническом обслуживании; — математическое ожидание времени, затрачиваемого на плановые и неплановые ремонты.

Коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относи­тельно рассматриваемой продолжительности эксплуатации. Пе­риод эксплуатации, для которого определяется 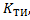должен, как правило, содержать все виды технического обслуживания и ре­монтов. Коэффициент технического использования учитывает за­траты времени на плановые и неплановые ремонты.

Коэффициент планируемого применения представляет собой долю периода эксплуатации, в течение которой объект не должен находиться на плановом техническом обслуживании и ремонте, т. е. это отношение разности заданной продолжительности экс­плуатации 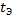и математического ожидания суммарной продолжи­тельности плановых технических обслуживании 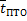и ремонтов 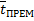за тот же период эксплуатации к значению этого периода:

(1.32)

Коэффициент сохранения эффективности — это отношение значения показателя эффективности за определенную продолжи­тельность эксплуатации Э к номинальному значению этого показа­теля , вычисленному при условии, что отказы объекта в течение того же периода эксплуатации не возникают. Данный коэффици­ент характеризует степень влияния отказов элементов объекта на эффективность его применения по назначению:

(1.33)

При этом под эффективностью применения объекта по на­значению понимают его свойство создавать некоторый полезный результат (выходной эффект) в течение периода эксплуатации в определенных условиях. Эффективность, как свойство объекта, характеризуется соответствующими показателями. Показатель эффективности — показатель качества, характеризующий вы­полнение объектом его функций. В идеальном случае объект вы­полняет свои функции (создает определенный выходной эффект) при отсутствии отказов. Реальный выходной эффект определя­ют с учетом реальной надежности Э. Аналитические выражения для расчета эффекта для различных типов объектов приведены в ГОСТ 27.003-89.

В некоторых отраслях техники изменяются комплексные по­казатели надежности, отражающие специфику эксплуатации обо­рудования отрасли. Так, в ядерной энергетике при оценке надеж­ности ядерной энергетической установки распространение получил коэффициент использования установленной мощности, который представляет собой отношение фактически выработанной мощно­сти за время 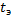к мощности, которую она выработала бы за это же время, работая на номинальной мощности W_H без остановок:

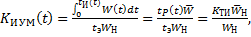(1.34)

где 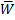— средний уровень мощности ЯЭУ за время 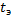(исключая время остановок).

Коэффициент установленной мощности также можно исполь­зовать при оценке надежности ЭА. Тогда за фактическую мощ­ность следует принимать мощность, выработанную в утяжеленном режиме работы за время .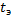

Номинальная мощность — это мощность, выработанная за вре­мя 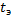при работе ЭА в режиме номинального тока.

Выбор номенклатуры показателей надежностей и их нормиро­вания осуществляется на основании ГОСТ 27.033-83 [5].

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: