Основные операции с множествами

Нетрудно убедиться, что операции пересечения, соединения и дополнения обладают следующими свойствами:

1. Коммутативность (переместительный закон) — свойство сло­жения и умножения чисел, выраженное тождеством а + b = b + а, ab = ba. Векторное умножение не является коммутативным. Для опе­раций логическая коммутативность выглядит следующим образом:

(2.4)

2. Ассоциативность (сочетательный закон, свойство сложения и умножения чисел, выраженное тождествами (а + b) + с = а + (b + с) и (ab)c = а(bс), скалярное, но не векторное (матрицы, век­торы — ). Применительно к множествам:

(2.5)

3. Дистрибутивность (распределительный закон, свойство сло­жения и умножения, с(а + b) = са + cb, F(xy) = F(x)F(y), = . Оператор возведения в степень дистрибутивен относительно опе­рации возведения в степень:

(2.6)

4. Идемпотентность:

(2.7)

5. Закон двойного отрицания:

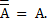
6. Правило де Моргана:

(2.9)

7. Закон логического противоречия:

(2.10)

8. Закон исключенного третьего:

(2.11)

где X — унитарное множество.

9. Операция с унитарным множеством X и пустым множест­вом ϕ:

(2.12)

2.4.

ГРАФИЧЕСКИЕ МЕТОДЫ

ПРОВЕРКИ ФОРМУЛ АЛГЕБРЫ МНОЖЕСТВ

Формулы алгебры множеств могут быть проверены с помощью карт Карно [23] и диаграмм Венна, этот способ рассмотрим ниже. Множества, за исключением полного множества, будем обозначать с помощью кругов. Когда имеем дело с двумя множествами А, В, рисуем два пересекающихся круга, из которых один символизирует множество А, а другой — В, получая тем самым диаграмму (рис. 2.1).

Рис. 2.1 Два пересекаю­щихся множества

Произведение АВ символизируется частью плоскости 1, разность А- В — частью плоско­сти 2, а сумма А + В — частью плоскости, обра­зованной 1...3.

Для символического представления дополнения множества вводим

Рис. 2.2 Множество А' дополняет множество А

прямоугольник Q, соответствующий полному множеству. Помещая в этом прямоугольнике круг, символизирующий мно­жество А, получаем диаграмму, где часть пря­моугольника, находящаяся вне круга, соот­ветствующего множеству А, символически представляет дополнение этого множества, т. е. множество А' (рис. 2.2).

Множество А содержится в множестве В тогда и только тогда, когда часть плоскости, символизирующая А, находится в части плос­кости, символизирующей В, или же совпада­ет с последней.

Имея в виду сказанное, легко по рис. 2.1 прочитать следую­щие формулы:

— соответствует закону коммутативности;

Множество А равно множеству й тогда и только тогда, когда плоскость, символизирующая множество А, совмещается с плос­костью, символизирующей множество В, и наоборот. Поэтому (рис. 2.2) очевидно, что верны формулы:

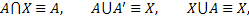
Выражение

проверяем, нарисовав диаграмму (рис. 2.3) и заштриховав на ней сначала часть плоскости, символизирующую множество A U В ⋂ С, а затем часть плоскости, символизирующую (A ⋃ В)⋂(A U С).

Для левой части проверяемого равенства получаем диаграмму (рис. 2.4), где заштрихованная часть плоскости символизирует множество A U В ⋂ С.

Для правой стороны этого равенства (A U В) ⋂ (A U С) получаем диаграмму на рис. 2.5.

Часть плоскости, заштрихованная горизонтальными черточка­ми, символизирует здесь множество A U В, вертикальными — мно­жество А + С, их общая часть, заштрихованная дважды, символи­чески представляет произведение (A U В) ⋂ (AU С). Так как части плоскости, символизирующие множества А ⋃ В ⋂ С и (А + В)(А + С), совпадают, то эти множества равны, а потому проверяемое выраже­ние истинно.

(Непрерывные линии используются для обозначения пустого множества: так отмечена, например, истинность выражения А ⊂ В на диаграмме рис. 2.1.)

В силу приведенных выше разъяснений вы­ражение A ⊂ Вистинно тогда и только тогда, когда часть плоскости, символизирующая мно­жество А, находится в части плоскости, симво­лизирующей множество В (или совпадает с этой последней частью плоскости). Что имеет место тогда и только тогда, когда множество А- В, символически представляемое частью 2 плоско­сти, пусто.

Таким образом, истинность выражения А ⊂ В иллюстрируем с помощью диаграммы на рис. 2.6, а выражения A ⊄ В — на рис. 2.7.

С помощью диаграммы Венна можно анали­зировать выражения, содержащие четыре пе­ременные, тогда строятся четыре пересекаю­щиеся окружности. Такая диаграмма в качест­ве обобщения графического метода проверки была выполнена профессором Лушчевской-Романовой [21].

 

2.5.

ОБЩИЕ ВОПРОСЫ ТЕОРИИ МНОЖЕСТВ

Множество может быть конечным:

Например, множество С точек на плоскости, лежащих внутри или на границе круга с центром в начале координат, может быть записано в виде

где х, у — декартовы координаты точки; R — радиус круга.

Множество

— бесконечно.

Бесконечное множество называется счетным, если все его члены можно перечислить в определенной последовательности: , ,... Множество С точек внутри и на границе круга радиу­са R>0:

является бесконечным и несчетным (его элементы нельзя перену­меровать один за другим). Пустое множество:

Все пустые множества эквивалентны друг другу.

Следует отметить, что в теории вероятностей используется не­сколько иная символика для взаимоотношений множеств.

Объединение множеств С = А + В (ранее С = A U В). Аналогично

— бесконечное, не счетное число множеств.

Пересечение множеств D = АВ (ранее D = А ⋂ В). Множество

— счетное множество.

 

Как и при записи обычного умножения, знак умножения в про­изведении событий часто опускается: D = АВ.

Этих элементарных сведений по теории множеств достаточно для того, чтобы пользоваться теоретико-множественной схемой построения теории вероятностей.

Пример 1. Пусть А, В и С — области на плоскости хОу, опре­деляемые неравенствами:

— круг радиуса 2; — верхняя полуплоскость;

— круг радиуса 1(рис. 2.8).

Легко проверить, что множества и совпадают и определяют область S (заштрихованная). всех пар (а, b), где а и b независимо друг от друга принимают все значения соответственно из множеств А и В. Эта область называется декартовым произведением множеств А и В и обозначается через АВ. Если А и В — конечные множества, содержащие соответственно т и п элементов, то множество АВ со­держит тп элементов.

Назовем область всех упорядочен­ных пар элементов из А де­картовым квадратом множества А и будем обозначать его А².

Рис. 2.8 Области А, В и С

С точки зрения теории мно­жеств натуральные кардиналь­ные числа отвечают классам равномощных конечных множеств, к ним, естественно, присоединяется

 

 

Рис. 2.9

Сложении непересекающихся областей

и нуль как кардинальное число, соответствующее пустому мно­жеству. Тогда элементарные отношения и действия над натураль­ными числами вводятся следующим образом.

1. Отношение «равно», «больше», «меньше»: т и п — два на­туральных числа; М и N — множества, т = п — множества, М и N равномощны

2. Сложение. Для определения суммы кардинальных чисел поступают так. Пусть m и n — два натуральных числа. Выбираем опять произвольно два непересекающихся множества М ⊂ т, где на рис. 2.9 a пунктиром обозначены участки границы области S,
не принадлежащей S, а на рис. 2.9 б представлен результат сложения т. е.

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Какими основными элементами оперирует теория множеств?

2. Какие операции с множествами можно считать основными?

3. Какими свойствами обладают операции пересечения, соединения и дополнения?

4. Какое свойство при работе с множествами называется коммутатив­ным?

5. Какое свойство при работе с множествами называется ассоциативным?

6. Какое свойство при работе с множествами называется дистрибутивным?

7. С помощью каких графических методов можно осуществить провер­ку формул алгебры множеств?

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: