Высказывания и булевы функции

Одной из основных задач алгебры высказываний является ус­тановление значения истинности сложных высказываний в зави­симости от значения истинности входящих в них простых выска­зываний. Для этого целесообразно рассматривать сложные выска­зывания как функции входящих в них простых высказываний. С другой стороны, так как значение истинности (˄ или ˄) сложно­го высказывания зависит по определению логических связок не от самих простых высказываний, а лишь от их значения истинно­сти, то можно считать, что любое сложное высказывание опреде­ляет функцию, аргументы которой независимо друг от друга при­нимают значения И или Л, а значение самой функции также при­надлежит множеству (И, Л), которое зачастую обозначают через {1, 0}. Такие функции называются булевыми функциями (по име­ни Д. Буля). Например, формула опи­сывает, учитывая определение входящих в нее связок, булеву функцию, задаваемую таблицей.

ЭА при рабочих нагрузках должен надежно работать в трех режимах: длительном (год и больше), соответствующем номиналь­ному току; кратковременном и повторно-кратковременном. Ука­занные три режима равновероятны и независимы друг от друга. Однако предельная величина нагрева частей аппарата при всех режимах не должна быть выше допустимого превышения темпе­ратуры над окружающей средой.

Заметим, что булевых функций от п аргументов имеется лишь конечное число, именно столько, сколько возможно функциональ­ных таблиц. Число возможных наборов аргументов равно , а ка­ждому набору аргументов можно независимо друг от друга сопо­ставлять одно из значений: 1 или 0. Таким образом, число всевоз­можных булевых функций от п аргументов равно . Оно быстро растет с ростом п.

Изучение свойств булевых функций приобретает все большее значение как для алгебры и математической логики, так и для их приложений в кибернетике и теории автоматов. Естественно рас­пространить определение высказываемых ранее связок на булевы функции связок ˄, ˅,, называемых булевыми связками (булевы­ми операциями). Такое ограничение оправдано тем, что, как лег­ко проверить, связки ⇒ и ⇔ могут быть выражены через другие булевы связки. При помощи таблиц истинности, приведенных выше, легко проверяются следующие тождества:

которые позволяют повсеместно заменить связки ⇒, ⇔ на ⋂, ⋃ ,. Если мы теперь будем иметь булевы функции , то действия над ними определяются естествен­ным образом:

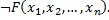
Это такие булевы функции, которые принимают значения, предписываемые соответствующими таблицами для каждого воз­можного значения аргументов.

Булевы операции так переносятся на булевы функции, как действия арифметики переносятся на обычные функции число­вых аргументов. При этом можно отметить, что в одном опреде­ленном смысле алгебра булевых функций проще алгебры чи­словых функций: если рассматривать лишь функции некоторо­го конечного числа аргументов, то таких функций конечное число.

Законы булевой алгебры. Обозначим объекты, над которыми осуществляются булевы операции ˅, ˄,: А, В, С,..., X, У, Z. Для определенности будем считать, что эти объекты — булевы функ­ции некоторого фиксированного числа переменных. Тогда

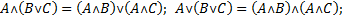
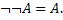
Если булевы операции ˅, ˄,, считать аналогом сложения, ум­ножения и перехода к противоположному числу (в электротехни­ке и в вычислительной технике принято говорить о логическом сложении и умножении и употреблять + «u»), то некоторые из вышеприведенных законов те же, что для числового сложения и умножения, остальные существенно отличаются.

3.4.