 |
Основные логические операции
|
|
|
|
Отрицание высказывания А обозначается символом А' (не А). Значение истинности высказывания А определяется таблицей:

Таким образом, отрицанием высказывания А является сложное высказывание А', которое ложно, когда А истинно, и истинно, когда А ложно.
Конъюнкция, или логическое умножение, высказываний Л и Вобозначается символом А и В (иногда А ˄ В, АВ ). Значение истинности логического произведения А & Вопределяется в зависимости от значений истинности высказываний А и В по следующей таблице:
| 0 ˄ 0 = 0 0 ˄ 1 = 0 1 ˄ 0 = 0 1 ˄ 1 = 1 |
Конъюнкция А ˄ Вдвух высказываний представляет собой сложное высказывание, которое истинно тогда и только тогда, когда истинны составляющие его высказывания А и В.
Дизъюнкция, или логическое сложение, двух высказываний А и Вобозначается символом
А ˅ В(читается А или В). Значение истинности логической суммы А ˅ Вв зависимости от значений определяется по таблице:
| 0 ˅ 0 = 0 0 ˅ 1 = 1 1 ˅ 0 = 1 1 ˅ 1 = 1 |
Дизъюнкция двух высказываний А и Вявляется сложным высказыванием, которое ложно тогда и только тогда, когда оба слагаемых А и Вложны.
Приведенные выше логические операции не являются независимыми и могут выражаться друг через друга. Преобразования логических выражений выполняются по определенным правилам.
Правила для одной переменной:
1.  ; 2.
; 2. 
З.  4.
4. 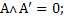
5.  6.
6. 
7.  8.
8. 
9.  10.
10.  .
.
Правила (1)...(10) легко доказываются простой подстановкой вместо А 1 и 0.
Как следствие из правил (3) и (7) имеем

В отличие от обычной алгебры, в алгебре логики «умножение переменной самой на себя» или «приведение подобных членов» осуществляется согласно перечисленным тождествам без появления каких бы то ни было показателей степени или коэффициентов.
|
|
|
Правила для двух и трех переменных:
11. 
12.  а также переместительный (или коммутативный) закон.
а также переместительный (или коммутативный) закон.
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам операций умножения и сложения. Легко убедиться в том, что для этих функций имеет место сочетательный (или ассоциативный) закон:
13. 
1А.  .
.
Правила (11)...(14) выражают свойства конъюнкций и дизъюнкций, взятых в отдельности.
В силу справедливости для логического умножения и сложения сочетательного и переместительного законов выражения, в которые входят конъюнкции и дизъюнкции, можно писать без скобок. При этом принимают соглашение считать связь с помощью знака ˄ (&) более тесной, чем ˅. Тем самым в алгебре логики устанавливается правило записи выражений, аналогичное принятому в обычной алгебре (в процессе вычислений «старшие» действия выполняются раньше «младших»). Это соглашение позволяет вместо  писать
писать 
Рассмотрим правила, выражающие связь между операциями логического умножения и сложения, взятыми совместно. Молено доказать, что для этих функций имеет место распределительный (или дистрибутивный) закон конъюнкции относительно дизъюнкции:
15. 
и распределительный закон дизъюнкции относительно конъюнкции:
16. 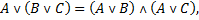
который в обычной алгебре не имеет места. Действительно,

Необходимо заметить, что все три названных закона обладают симметрией в том смысле, что из любого закона для дизъюнкции (конъюнкции) можно получить путем замены знаков дизъюнкции на знаки конъюнкции и знаков конъюнкции на знаки дизъюнкции соответствующий закон для конъюнкции (дизъюнкции). Действительно, взяв, например, выражение

и произведя замену знаков, получим

Следующий закон, известный в литературе под названием закона двойственности или инверсий, позволяет заменять отрицание конъюнкции дизъюнкцией отрицаний и отрицание дизъюнкции конъюнкцией отрицаний:
|
|
|
17.  ;
;

Если к правилам (17) и (18) применить правило (9), то получим
19. 
20. 
Правила (19)...(20), названные в честь одного из основоположников математической логики английского ученого де Моргана формулами де Моргана, позволяют логическое умножение выражать через отрицание логической суммы из инверсных высказываний, а логическую сумму — через отрицание логического произведения из инверсных высказываний. Формулы (19)...(20) легко обобщаются на произвольное число логических переменных:

где логические переменные обозначены х с различными индексами 1(1 е [1, п]), а знаки конъюнкций и дизъюнкций использованы аналогично знакам произведения П и суммы 2, применяемым в обычной алгебре.
 На основании четырех рассмотренных выше законов можно установить ряд других полезных отношений, позволяющих существенно упростить сложные логические выражения.
На основании четырех рассмотренных выше законов можно установить ряд других полезных отношений, позволяющих существенно упростить сложные логические выражения.
Познакомимся с операциями поглощения и склеивания.
Операция поглощения определяется соотношениями
 21.
21. 
22. 
Используя терминологию теории множеств, будем говорить, что подмножеством А поглощается множеством B, если A⊂ B (рис. 3.1).

Как следует из (21)...(22) в первом случае (А ˄ В) ⊂ A, а во втором—  . На рис. 3.1, иллюстрирующем (21)...(22), поглощаемые подмножества заштрихованы, а поглощающие множества выделены контуром.
. На рис. 3.1, иллюстрирующем (21)...(22), поглощаемые подмножества заштрихованы, а поглощающие множества выделены контуром.
Операция склеивания определяется соотношениями


где использована запись операции логического умножения без знака конъюнкции.
Графическая иллюстрация соотношений (23)...(24) дана на рис. 3.2, 3.3.
Упростим теперь выражение А ˄ (А ' ˅ В). На основании распределительного закона конъюнкции относительно дизъюнкции (15) имеем

По правилу (4) А ˄ А' = 0, следовательно,

Используя правило (6), окончательно получаем
25. 
Аналогично
26. 
Остановимся на ряде определений и обозначений, которые потребуются в процессе изучения курса.
Рассмотрим степень аргумента  , которую обозначим
, которую обозначим  , где
, где  — двоичная переменная величина. Положим, что
— двоичная переменная величина. Положим, что

Условимся переменные  и их отрицания
и их отрицания  ' (i = 1,2,..., п)называть буквами, а i — номером или индексом переменной.
' (i = 1,2,..., п)называть буквами, а i — номером или индексом переменной.
Определение 1. Выражение вида  называется элементарной конъюнкцией (К) ранга r. В силу того, что
называется элементарной конъюнкцией (К) ранга r. В силу того, что  и
и  все буквы в элементарной конъюнкции различны.
все буквы в элементарной конъюнкции различны.
|
|
|
Определение 2. Выражение вида

где  — элементарные конъюнкции различных рангов, называется дизъюнктивной нормальной формой (ДНФ).
— элементарные конъюнкции различных рангов, называется дизъюнктивной нормальной формой (ДНФ).
Например, функция

записана в ДНФ, так как все три слагаемых являются элементарными конъюнкциями.
Определение 3. Если функция  записана в ДНФ, причем ранг каждой элементарной конъюнкции равен п, то такая ДНФ называется совершенной ДНФ (СДНФ), а конъюнкции — членами СДНФ или конституентами единицы.
записана в ДНФ, причем ранг каждой элементарной конъюнкции равен п, то такая ДНФ называется совершенной ДНФ (СДНФ), а конъюнкции — членами СДНФ или конституентами единицы.
Любая функция алгебры логики (ФАЛ) может быть записана в СДНФ в виде

где  — член СДНФ с j -м номером, и суммирование ведется по всем наборам, на которых функция
— член СДНФ с j -м номером, и суммирование ведется по всем наборам, на которых функция  равна единице.
равна единице.
Определение 4. Выражение вида 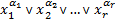 называется элементарной дизъюнкцией (D) ранга r.
называется элементарной дизъюнкцией (D) ранга r.
Определение 5. Выражение вида

где  — элементарные дизъюнкции различных рангов, называется конъюнктивной нормальной формой (КНФ).
— элементарные дизъюнкции различных рангов, называется конъюнктивной нормальной формой (КНФ).
Определение 6. Если функция  записана в КНФ и ранг каждой элементарной дизъюнкции равен п, то такая КНФ называется совершенной КНФ (СКНФ), а дизъюнкции — членами СКНФ или конституентами нуля.
записана в КНФ и ранг каждой элементарной дизъюнкции равен п, то такая КНФ называется совершенной КНФ (СКНФ), а дизъюнкции — членами СКНФ или конституентами нуля.
Любая ФАЛ может быть записана в СКНФ в виде

где  — член СКНФ с j -м номером и произведение ведется по всем наборам, на которых функция
— член СКНФ с j -м номером и произведение ведется по всем наборам, на которых функция  равна нулю.
равна нулю.
Определение 7.Две элементарные конъюнкции называются ортогональными, если их произведение равно нулю. Например, произведение элементарных конъюнкций  и
и  равно нулю, так как одна из них содержит
равно нулю, так как одна из них содержит  , а другая —
, а другая —  .
.
Определение 8. ДНФ называется ортогональной ДНФ (ОДНФ), если все ее члены попарно ортогональны. В соответствии с этим определением СДНФ является ОДНФ, так как все ее члены попарно ортогональны. Но СДНФ является самой неэкономной из всех ОДНФ, так как она содержит максимальное количество букв.
Определение 9. Бесповторной ДНФ (БДНФ) называется такая ДНФ, в которой все буквы имеют разные номера. Буквы  и
и  имеют один и тот же номер, поэтому они не могут одновременно входить в БДНФ.
имеют один и тот же номер, поэтому они не могут одновременно входить в БДНФ.
Определение 10. Бесповторной формой ФАЛ называется такая форма, в которой все буквы имеют разные номера. Частным случаем бесиовторной формы ФАЛ является БДНФ. Например, функция
|
|
|

записана в бесповторной форме, так как все буквы имеют разные номера.
Функции алгебры логики могут быть представлены в табличной форме, в виде аналитической записи в строку, а также в виде логических матриц. В частности, логические матрицы конъюнкции для записи логических уравнений представляются в виде логических символов в строке, а дизъюнкции — их расположением в столбце.
К логическим матрицам применимы все преобразования алгебры логики. Так, переместительный закон конъюнкции допускает перестановку логических символов в строке, а переместительный закон дизъюнкции — в столбце.
Пусть функции алгебры логики имеют вид
 (3.1)
(3.1)
В матричной форме (3.1) может быть представлено в виде
 (3.2)
(3.2)
Вторая матрица (3.2) записана в ДНФ.
При приведении к нормальной форме логические матрицы упрощаются. Например, используя распределительный закон конъюнкции, получаем выражение
 (3.3)
(3.3)
Применяя закон инверсии, находим
 (3.4)
(3.4)
Как видно из формулы (3.4), инверсия логических матриц осуществляется заменой конъюнктивных связей логических символов в строке на дизъюнктивные связи отрицания этих символов, располагаемых в столбце, а дизъюнктивных связей между строками — на конъюнктивные связи между столбцами, образованными из этих строк. Подробней с элементами математической логики можно ознакомится, прочитав [26].
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Назовите основные логические связки.
2. Каким знаком обозначается связка конъюнкция, и что она означает?
3. Каким знаком обозначается связка дизъюнкция, и что она означает?
4. Каким знаком обозначается связка импликация, и что она означает?
5. Каким знаком обозначается связка эквиваленция, и что она означает?
6. В чем состоит основная задача алгебры высказываний?
7. Назовите основные логические операции.
8. В чем заключается операция поглощения?
9. В чем заключается операция склеивания?
|
|
|


