Основные логические связки

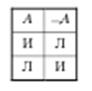Отрицание (знак ­). Если А — высказывание, то 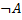(читается: не А) также высказывание; оно истинно или ложно в зависимости от того, ложно или истинно высказывание А. Видим, что опера­ция в теории высказываний вполне соответствует понятию от­рицания в обыденном смысле слова. Операция отрицания может быть описана таблицей

Конъюнкция. В качестве знака для конъюнкции употребляет­ся знак л, а также & (иными словами, союз and — и).

Если А и В — высказывания, то А ˄ В (читается: А и В) — но­вое высказывание. Оно истинно тогда и только тогда, когда А ис­тинно и В истинно.

В отличие от операции отрицания, зависящей от одного эле­ментарного высказывания, конъюнкция, как и все последующие приводимые нами связки, зависит от двух элементарных выска­зываний, поэтому они называются двуместными связками, отри­цание же — связка одноместная.

Для задания двухместных связок удобно записывать матрицы истинности в виде таблиц с двумя входами: строки соответствуют значениям истинности одного элементарного высказывания, столб­цы — значениям другого элементарного высказывания, а в клетке пересечения столбца и строки помещается значение истинности соответствующего сложного высказывания.

Значение истинности сложного высказывания А ˄ В задается матрицей:

Как видно, определение операции конъюнкции вполне соот­ветствует обыденному значению союза «u». Например, проблема защищенности автоматизированных линий от возникновения ава­рии существенно зависит от надежности работы ЭА. Влияние виб­раций, возникающих при замыкании контактов, на коммутаци­онную износостойкость ЭА регулируется соотношением механи­ческой и тяговой характеристик электромагнитного привода.

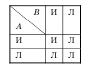
Дизъюнкция. В качестве знака для дизъюнкции употребим знак ˅. Если Аи В — высказывания, то A v В (читается: А или В) — новое высказывание. Оно ложное, если А и В ложны; во всех ос­тальных случаях A v В истинно. Таким образом, матрица истин­ности для операции дизъюнкции выглядит так:

Операция дизъюнкции соответствует обычному значению сою­за «или». Например, контроль износа контактов осуществляется выбором провала или взвешиванием до и после работы контактов на весах.

Импликация. В качестве знака для импликации будем упот­реблять знак 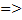. Если А и В — два высказывания, то А 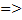В (чита­ется: А имплицирует В) — новое высказывание. Оно всегда истин­но, кроме того случая, когда А истинно, а В ложно.

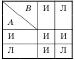
Матрица истинности операции импликации следующая:

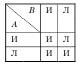
В импликации А 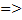В первый член А называется антецедентом, второй член В —консеквентном.

Импликация описывает в некоторой мере то, что в обыденной речи выражается словами «если А, то В», «из А следует В», «А — достаточное условие для В».

Если нарастание сопротивления в межконтактном промежут­ке после прохождения тока через нуль проходит интенсивнее, чем нарастание напряжения, то повторного зажигания дуги не про­изойдет. Если ток короткого замыкания 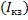значительно превы­шает ток плавления 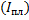плавкой вставки, то плавкая вставка пе­регорает и предохранитель отключает электрическую цепь.

Эквиваленция. Для этой операции употребляется знак ⇔. Опе­рация определяется так: если А и В — высказывания, то А ⇔ В (чи­тается: А эквивалентно В) — новое высказывание, которое истин­но, если либо оба высказывания истинны, либо оба ложны.

С помощью введенных связок можно строить сложные выска­зывания, зависящие не только от двух, но и от любого числа эле­ментарных высказываний.

В режимах номинальных токов 25...600 А пара контактов мо­жет выполнять двойную роль: длительное пропускание тока во включенном положении и отключение, сопровождающееся воз­никновением дуги. В первом случае контакты должны иметь ма­лое переходное сопротивление; во втором — накладываются тре­бования высокого переходного сопротивления. В обоих случаях применяют одну и ту же одноступенчатую контактную систему. Оба процесса влияют на износ контактов.

Примечание. Нестрогое неравенство 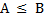представляет собой дизъюнкцию А<В ˅ (А = В).Оно истинно, если истинно по мень­шей мере одно из входящих в него простых высказываний. При­мерами сложных высказываний, встречающихся в практике, яв­ляются так называемые двойные неравенства А< В < С(А < В) ˄ (В < С), а, например, 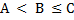означает сложное высказывание (А< В) ˄ ((В <C) ˅ (В = С)).Делается это аналогично тому, как в элементарной алгебре с помощью операций сложения, вычитания, умножения и деления строятся сколь угодно сложные рациональ­ные выражения.

Располагая значением истинности простых высказываний, легко подсчитать на основании определения связок значение ис­тинности сложного высказывания. Пусть дано сложное высказы­вание ((В ˅ С) ⇔ (В ˄ А)) и пусть входящие в него элементарные высказывания имеют следующие значения истинности: А = Л, В = И, С = И. Тогда В ˅ С= И, В ˄ А = Л, так что рассматриваемое высказывание ((В ˅ С) ⇔ (В ˄ А)) ложно.

3.3.