Оценки средней наработки до первого отказа и наработки на отказ

Числовые характеристики случайных величин, используемых в теории надежности, играют большую роль. С их помощью удает­ся компактно выразить наиболее существенные черты соответст­вующих распределений. Важнейшей числовой характеристикой, как известно, является математическое ожидание случайной ве­личины М[Т]. Оно характеризует среднее значение случайной ве­личины, около которого группируются возможные ее значения.

В теории надежности обычно рассматриваются следующие математические ожидания: средняя наработка до первого отказа , наработка на отказ (среднее значение наработки ремонтируемого изделия между отказами) , среднее время восстановления , среднее время между восстановлениями (отказами) , средняя длительность межпрофилактического периода , средняя дли­тельность профилактики и др.

Характеристикой рассеивания, разбросанности значений слу­чайной величины около ее математического ожидания служит дисперсия D[T] или среднеквадратичное отклонение случайной величины Среднее время и дисперсия могут быть найдены по результатам наблюдения случайных величин в виде точечной или интервальной оценки.

Любое значение искомой числовой характеристики, вычис­ленной на основе ограниченного числа наблюдений, будет содер­жать элемент случайности. Такое приближенное, случайное зна­чение назовем оценкой числовой характеристики М или D, обо­значая ее той же буквой, но с волнистой чертой (тильдой) наверху:

, .

Пусть имеется случайная величина Т с математическим ожи­данием М[Т] и дисперсией D[T), которые неизвестны. Наблюдае­мые значения случайной величины Т оказались равными , ,... Точечные оценки для характеристик М[Т] и D[T] составят:

(4.84)

(4.85)

где - статистическое среднее и статистическая дисперсия случайной величины T.

При малом числе наблюдений точечные оценки и [T] в значительной мере случайны и приближенная замена [Т] на М[Т], [T] на D[T] может привести к значительным погрешностям.

Чтобы дать представление о точности оценок [Т] и [T], используют метод доверительных интервалов. Двусторонним до­верительным интервалом для математического ожидания М[Т] с коэффициентом доверия, не меньшим, чем δ₂, называется случай­ный интервал концы которого < зависят от ис­ходов наблюдений (τ_1; τ₂,..., ) и для любого T

(4.86)

Верхним (0, ) и нижним ( односторонними доверительными интервалами называются такие случайные интервалы для которых при любом

(4.87)

(4.88)

Аналогично определяются доверительные интервалы и для дисперсии

Теперь найдем доверительные границы и . Основная труд­ность состоит в том, что закон распределения оценки = зави­сит от закона распределения случайной величины Т, которая чаще всего заранее неизвестна. В математической статистике разрабо­таны точные и приближенные методы построения доверительных интервалов для параметров случайной величины. Для примене­ния точных методов необходимо знать заранее вид закона распре­деления величины Т, тогда как при использовании приближен­ных методов это необязательно.

Рассмотрим сначала приближенное решение задачи. Восполь­зуемся тем, что величина Т представляет собой сумму n незави­симых, одинаково распределенных случайных величин 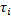_; и со­гласно предельной теореме при достаточно большом n ее закон распределения близок к нормальному.

Распределение случайной величины Y называется нормаль­ным, если соответствующая ей функция распределения выража­ется формулой

(4.89)

где a и σ – параметры распределения (|а|< математическое ожидание; среднеквадратичное отклонение); y может принимать все действующие значения.

Функция нормального распределения удовлетворяет равенству

(4.90)

поэтому для вычисления её значения достаточно иметь таблицу функций

(4.91)

или только таблицу так называемой нормированной функции Лапласа

(4.92)

На практике даже при относительно не большом числе слагаемых (порядка 10…..20) закон распределения величины можно приближенно считать нормальным с параметрами

(4.93)

(4.94)

Дисперсия D[T], как правило, неизвестна, в качестве её ориентировочного значения можно воспользоваться оценкой и положить

(4.95)

Зная теперь вид закона распределения случайной величины и его параметры, не трудно найти доверительные границы и для неизвестного математического ожидания .

Обозначим диапазон практически возможных случайных ошибок, возникающих при замене истинного значения параметра и его оценкой через

Тогда функции и можно выразить формулами

(4.96)

(4.97)

где наибольшая по абсолютной величине ошибка, гарантирующая с коэффициентом доверия выполнение не равенства

(4.98)

Выражение эквивалентно уравнению

(4.99)

разрешив которое относительно , определим искомые доверительные границы и .

Вероятность попадания случайной величины , подчинённой нормальному закону с параметрам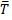и и , на участок 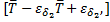составит

где

- аргумент нормированной функции Лапласа.

Из уравнения

(4.101)

находим значение

(4.102)

Где 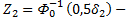функция, обратная функции Лапласа, т. е. такое значение аргумента для которого нормированная функция Лапласа равна .

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: