Дискретные распределения случайных величин в теории надежности

 

Дискретные распределения случайных величин, используемые в теории надежности, приведены в таблице 4.2.

Случайная величина ξ, имеет распределение Бернулли с пара­метром если Это распреде­ление играет фундаментальную роль в теории вероятностей и мате­матической статистике, являясь моделью для любого случайного эксперимента, исходы которого принадлежат двум взаимно ис­ключающим классам (либо отказ, либо работоспособное состоя­ние объекта).

Таблица 4.2 Нормированная таблица Лапласа Ф(z)

Случайная величина ξ, имеет биномиальное распределение с параметрами

если

(4.47)

где Р имеет смысл вероятности появления (или устранения) одно­го отказа в одном испытании;

k — число отказов в п независимых испытаниях; число сочетаний k отказов из п испытаний.

Биномиальное распределение является моделью случайных экспериментов, состоящих из п независимых однородных испы­таний Бернулли: если независимы и имеют распреде­ление Бернулли с параметром р,то случайная величина

имеет биномиальное распределение. Если р таково, что то можно пользоваться следующей приближенной формулой:

Если при то ошибка при использовании нормаль­ной функции распределения вместо биномиальной не превосхо­дит 0,05 при всех х. Если же р имеет одинаковый с 1/п порядок при больших п либо р < 0,1, можно использовать приближение распределением Пуассона

(4.48)

Математическое ожидание случайной величины k для биноми­ального распределения

M(k) = пр, дисперсия D (k) = σ² { k }= npq, q = 1 - p, коэффициент вариации

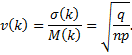
Для упрощения вычислений вероятностей имеются готовые таблицы. Как видно из выражения (4.47), в биномиальный закон входят три параметра: постоянные п и р ипеременная величина k.

Распределение Паскаля (отрицательное биномиальное рас­пределение) с параметрами

(r, р) при натуральном r описывает число испытаний в схеме Бернулли, необходимых для того, чтобы получить значение 1 ровно r раз. Пусть η — случайная величина, имеющая распределение Пуассона с параметром μ, т. е.

Будем рассматривать μ как случайную величину, имеющую гамма-распределение с параметром 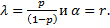Тогда

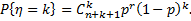(4.49)

В такой интерпретации распределение Паскаля имеет прило­жения к статистике отказов, к задачам медицины и биологии.

Важность геометрического распределения объясняется при­менением его к объектам и процессам с отсутствием последейст­вия: для любых

(4.50)

Типичная схема, в которой появляется гипергеометрическое распределение, такова: проверяется партия готовой продукции, которая содержит Np годных и N (1 - p) негодных объектов. Слу­чайным образом выбирают п объектов. Число годных объектов сре­ди выбранных и описывается гипергеометрическим распределени­ем. Если п мало по сравнению с N (практически когда п < 0,1 N), то

(4.51)

Распределение Пуассона является приемлемой моделью для описания случайного числа отказов и восстановлений объектов в фиксированном промежутке времени. Если пр = а, то

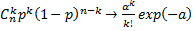. (4.52)

Для больших а имеет место приближение

(4.53)

где Ф(х) — нормальная (0, 1) функция распределения.

Если ξ, имеет распределение Пуассона спараметром а, то для больших а случайная величина 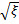имеет распределение, близ­кое к нормальному с параметрами Для распределения Пуассона имеем: математическое ожидание диспер­сию и коэффициент вариации Распре­деление Пуассона безгранично делимо: если сумма независимых случайных величин распределена по закону Пуассона, то и каж­дое слагаемое распределено по этому закону.

Логарифмическое распределение является предельным для распределения Паскаля. Если 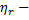случайная величина, имеющая распределение Паскаля с параметром (r, р),то

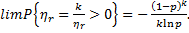(4.54)

Логарифмическим называют также распределение случайной величины ξ, у которой

(4.55)

Вырожденное распределение описывает неслучайные величи­ны. Верно обратное утверждение: если случайная величина ξ, име­ет конечное математическое ожидание и нулевую дисперсию, то

 

4.5.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: