Рекомендуемые для решения задачи

Задача 1. Плотность распределения наработки до отказа технических объектов имеет вид

Необходимо получить аналитические выражения для вычисления таких показателей надежности, как вероятность безотказной работы (ВБР), средняя наработка до отказа, параметр потока отказов.

Решение.

Вероятность безотказной работы вычисляется следующим образом.

Средняя наработка до отказа. Для вычисления параметра потока отказов используется уравнение Вольтерра, которое обычно решается с использованием преобразования Лапласа:

Средняя наработка до отказа:

Для вычисления параметра потока отказов используется урав­нение Вольтерра, которое обычно решается с использованием пре­образования Лапласа:

Вычислим f (s):

тогда преобразование Лапласа параметра потока отказов

Для отыскания 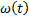найдем обратное преобразование Лапласа, предварительно разложив полученную дробь на простые дроби:

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ 2...44

Формула Бернулли (повторные независимые испытания). Если производится п независимых опытов, в каждом из которых вероятность появления события А равна Р, то вероятность того, что это событие при п опытах произойдет k раз, определяется формулой Бернулли

где q = 1 -p — вероятность не наступления события А в каждом испытании (она тоже постоянна).

Вероятность появления события хотя бы один раз при п опытах вычисляется следующим образом:

Вероятность появления события не менее т раз при п опытах вычисляется по формуле

Асимптотическая формула Пуассона. Распределение Пуассо­на, определяющее вероятность появления k событий простейшего потока событий за время t с интенсивностью λ, (λ — среднее число событий, появляющихся в единицу времени), имеет вид

В ряде задач вероятность наступления события р в отдельном испытании очень мала. Если при этом число испытаний п очень велико, то формула Бернулли превращается в асимптотическую формулу Пуассона

Локальная теорема Лапласа. При большом количестве повтор­ных испытаний в формуле Бернулли приходится оперировать очень большими числами. В этом случае удобнее использовать ло­кальную теорему Лапласа:

Интегральная теорема Лапласа. Гораздо чаще на практике возникает необходимость при п независимых испытаниях опре­делить вероятность того, что интересующее нас событие появится не менее k ₁и не более k ₂раз. Значение такой вероятности можно получить с использованием интегральной формулы Лапласа

где

— функция Лапласа, причем Ф(-х) = Ф(х);

 

ПРИМЕНЕНИЕ ПРИБЛИЖЕННЫХ ФОРМУЛ

ПУАССОНА И ЛАПЛАСА

1. Если число испытаний п = 10...20, то приближенные фор­мулы используются только для грубых расчетов; при этом форму­ла Пуассона применяется в том случае, когда пр изменяется в пре­делах от 0...2 (при п = 10) до 0...3 (при п = 20). В противном слу­чае необходимо пользоваться формулами Лапласа.

2. Если n = 10...20, то приближенные формулы уже можно ис­пользовать для прикладных расчетов. Формулу Пуассона рекомен­дуется применять, когда пр изменяется в пределах от 0...3 (при п = 20) до 0...5 (при п = 100).

3. Если n = 100...1000, то практически при любых расчетах можно обойтись приближенными формулами. Формула Пуассона применяется, когда пр изменяется в пределах от 0...5 (при п = 100)до 0…10(при n = 1000).

4. При п > 1000 даже специальные таблицы рассчитываются с помощью приближенных формул. В этом случае для применения формулы Пуассона необходимо, чтобы величина пр изменялась в пределах 0...10 и более.

 

Задача 2. В партии из п ЭА k штук бракованных. Определить вероятность того, что среди выбранных наудачу для проверки т изделий ровно l окажутся бракованными.

Решение.

Число возможных способов взять т ЭА из п равно При этом благоприятствующими являются те случаи, когда из общего числа k бракованных ЭА взято l штук (это можно сделать спо­собами), а остальные п - l ЭА не бракованные, т.е. они взяты из общего числа п - k (количество способов равно ). Поэтому чис­ло благоприятствующих случаев равно Искомая вероят­ность будет иметь вид

Задача 3. Микросхемы одного типа изготавливаются на трех заводах и поступают на сборку. Первый завод производит 20% всей продукции, второй — 30%, третий — 50%. В продукции первого завода 5% бракованных микросхем, второго — 3%, третьего — 2%. Взятая микросхема не удовлетворяет требованиям ОТК на сборке. Какова вероятность того, что эта микросхема изготовлена на первом заводе?

Решение.

Пусть событие А заключается в том, что взятая микросхема не удовлетворяет предъявляемым требованиям, тогда по формуле Байеса

Задача 4. Завод отправил потребителю 500 ЭА. Вероятность повреждения ЭА в пути равна 0,002. Найти вероятность того, что в пути будет повреждено: а) три ЭА, б) менее трех ЭА, в) более трех ЭА, г) хотя бы один ЭА.

Решение.

пр = 1, следовательно, применима формула Пуассона:

а) — вероятность повреждения трех ЭА;

б) найдем вероятность повреждения менее трех ЭА, т. е. может
быть повреждено либо 0 ЭА, либо 1 ЭА, либо 2 ЭА:

в) для нахождения вероятности повреждения более трех ЭА легче сначала вычислить вероятность противоположного события и тогда

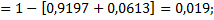
г) аналогично вычислим вероятность повреждения хотя бы од­ного ЭА:

Задача 5. Вероятность появления отказа в любой момент вре­мени промежутка Т равна p. Известно, что за время t < Т отказа не произошло. Определить вероятность Р того, что отказ произой­дет в оставшийся промежуток времени.

Решение.

Вероятность р появления отказа за время Т равна вероятно­сти появления отказа за время t плюс произведение веро­ятности того, что отказ не произойдет за время t, на условную вероятность появления отказа за оставшееся время приусловии, что он раньше не произошел. Таким образом, имеет ме­сто равенство

откуда находим

Задача 6. Из партии, в которой 30 деталей без дефекта и 5 с дефектом, берут наудачу 3 детали. Определить вероятность того что, по крайней мере одна деталь будет без дефекта.

Задача 7. Для перевозки (n + m)изделий двух типов использо­вался железнодорожный состав. Получена информация о том, что в пути следования повреждены два изделия. Определить вероят­ность того, что повреждены изделия различных типов.

Задача 8. При увеличении напряжения в два раза может про­изойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов соответ­ственно с вероятностями 0,3, 0,4 и 0,6. Определить вероятность того, что при этом не будет разрыва цепи. Как изменится искомая вероятность, если не будет первого элемента?

Задача 9. Определить вероятность того, что выбранное науда­чу изделие является первосортным, если известно, что 4% всей продукции — брак, а 75% не бракованных изделий удовлетворя­ют требованиям первого сорта.

Задача 10. Вероятность выхода из строя k -го блока ЭА за вре­мя t равна Определить вероятность выхода из строя за указанный промежуток времени хотя бы одного из блоков этого ЭА, если работа всех блоков взаимно независима.

Задача 11. Вероятность наступления события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до на­ступления события. Определить вероятность того, что придется проводить четвертый опыт.

Задача 12. Вероятность изготовления первосортной детали на первом станке равна 0,7, на втором — 0,8. На первом станке изго­товлены две детали, на втором — три. Найти вероятность того, что все детали первосортные.

Задача 13. Разрыв электрической цепи ЭА может произойти вследствие выхода из строя элемента К или двух элементов К ₁и К ₂(рис. 4.11). Вероятность выхода из строя элемента K равна 0,3, а для каждого из элементов К ₁и К ₂эти ве­роятности равны 0,2. Определить вероят­ность разрыва электрической цепи ЭА.

Задача 14. Работа ЭА прекратилась вследствие выхода из строя одного модуля из общего числа N. Определение этого мо­дуля производится путем поочередной замены каждого модуля но­вым. Найти вероятность того, что придется проверить п модулей, если вероятность выхода из строя каждого модуля равна q.

Задача 15. Вероятность превышения номинального значения напряжения в электрической цепи ЭА равна q ₁. При повышенном напряжении вероятность аварии ЭА — потребителя электрическо­го тока — равна q ₂. Определить вероятность аварии ЭА вследствие повышения напряжения.

Задача 16. Детали могут быть изготовлены с применением двух технологий: в первом случае деталь проходит три технологиче­ские операции; вероятности получения брака при каждой из них равны 0,1; 0,2 и 0,3. Во втором — имеются две операции, вероят­ности получения брака при которых одинаковы и равны 0,3. Оп­ределить, какая технология обеспечивает большую вероятность получения первосортной продукции, если в первом случае вероят­ность получения продукции первого сорта для не бракованной де­тали равна 0,9, а во втором — 0,8.

Задача 17. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, для первого станка равна 0,7; для второго — 0,8; для третьего — 0,9; для четвертого — 0,85. Найти вероятность того, что в течение часа по крайней мере один станок потребует к себе внимания рабочего.

Задача 18. Из партии п ЭА, среди которых r бракованных, науда­чу берутся r ЭА. Какова вероятность того, что все они бракованные?

Задача 19. Определить вероятность того, что партия из 100 ЭА, среди которых пять бракованных, будет принята при испытании наудачу выбранной половины всей партии, если условиями прие­ма допускается бракованных ЭА не более одного из 50.

Рис. 4.12 Схема электрической цепи

Задача 20. Электрическая цепь между точками А и Б составлена по схеме, которая представлена на рис. 4.12. Выход из строя за вре­мя t различных элементов цепи — независимые события, имеющие следующие вероятности:

Номер элемента
Вероятность выхода из строя	0,6	0,5	0,4	0,7	0,9

 

Задача 21. В результате опыта соответственно с вероятностя­ми 0,012; 0,10; 0,006 и 0,002 может произойти одно из четырех несовместных событий. Определить вероятность того, что в резуль­тате опыта произойдет любое из этих событий.

Задача 22. Селективный блок, встроенный в ЭА, может при­надлежать одной из трех партий с вероятностями где Вероятности того, что блок проработает заданное число часов для этих партий, равны соответственно 0,1; 0,2 и 0,4. Определить вероятность того, что блок проработал за­данное число часов.

Задача 23. Определить вероятность того, что 100 дросселей, взятых наудачу из 1000, окажутся исправными, если известно, что число исправных дросселей из 1000 штук равновозможно от 0 до 5.

Задача 24. Партия из 100 ЭА подвергается выборочному кон­тролю. Условием непригодности всей партии является наличие хотя бы одного бракованного ЭА среди пяти проверяемых. Какова вероятность для данной партии быть непринятой, если она содер­жит 5% неисправных ЭА?

Задача 25. Вероятность того, что реле останется исправным после 1000 ч работы, равна 0,2. Какова вероятность того, что хотя бы одно из трех реле останется исправным после 1000 ч работы?

Задача 26. На сборку попадают детали с трех автоматов. Из­вестно, что первый автомат дает 0,3% брака, второй — 0,2%, тре­тий — 0,4%. Найти вероятность попадания на сборку бракован­ной детали, если с первого автомата поступило 1000, со второго — 2000, с третьего — 2500 деталей.

Задача 27. Рабочий обслуживает три станка, на которых обра­батываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго — 0,03, для третьего — 0,04. Обра­ботанные детали складываются в один ящик. Производительность первого станка в 3 раза больше, чем второго, а третьего — в 2 раза меньше, чем второго. Определить вероятность того, что взятая нау­дачу деталь будет бракованная.

Задача 28. Завод выпускает три типа предохранителей для ком­пьютеров. Доля каждого из них в общем объеме составляет 30, 50 и 20% соответственно. При перегрузке сети предохранитель первого типа срабатывает с вероятностью 0,5, второго— 0,9, третьего — 0,85. Выбранный наудачу предохранитель не сработал при пере­грузке сети. Какова вероятность того, что он принадлежал к пер­вому, второму, третьему типу?

Задача 29. На фабрике, изготавливающей ЭА, первая поточ­ная линия производит 30%, вторая — 45%, третья — 25% всех ЭА. Брак составляет соответственно 2, 5 и 3% продукции. Найти вероятность того, что случайно выбранный ЭА произведен первой поточной линией, если он оказался дефектным.

Задача 30. Фирма имеет пять компьютеров. Вероятность того, что в течение трех лет каждый потребует ремонта, равна 0,2. Най­ти вероятность того, что в течение указанного срока не придется ремонтировать хотя бы два компьютера.

Задача 31. В помещении четыре электровыключателя. Для каждого из них вероятность оказаться исправным в течение года равна 5/6. Какова вероятность того, что в течение года придется заменить не меньше половины электровыключателей.

Задача 32. Вероятность выхода из строя за сутки одного кон­денсатора равна 0,2. Найти вероятность того, что за сутки из 100 независимо работающих конденсаторов выйдут из строя 20.

Задача 33. Автоматическая штамповка клемм для предохра­нителей дает 10% отклонений от принятого стандарта. Сколько стандартных клемм следует ожидать с вероятностью 0,0587 среди 400 клемм?

Задача 34. В результате проверки качества изготовленных микросхем установлено, что 90% всей продукции удовлетворя­ет всем требованиям нормативно-конструкторской документа­ции. Найти вероятность того, что среди 900 наудачу отобран­ных для испытания микросхем исправными окажутся от 600 до 640 штук.

Задача 35. Вероятность выпуска бракованной детали рав­на 0,005. Найти вероятность того, что среди 1000 деталей брако­ванных будет: а) 8; б) не более 2.

Задача 36. При работе компьютера возникают сбои в среднем 2 раза в сутки. Найти вероятность того, что: а) за двое суток не произойдет сбоя; б) в течение суток произойдет хотя бы один сбой; в) за трое суток произойдет не менее трех сбоев.

Задача 37. Определить основные показатели надежности под­систем обработки информации, распределение времени возникно­вения отказов которых подчиняется соответственно

а) закону Рэлея:

б) закону Вейбулла:

в) гамма-распределению:

Задача 38. Вероятность безотказной работы ЭА в течение t = 1000 ч равна 0,95. Время исправной работы подчинено зако­ну Рэлея. Требуется определить количественные характеристики надежности

Задача 39. Время исправной работы ЭА подчинено закону Вей­булла с параметрами a = 2,6; θ = 0,610⁷. Необходимо найти веро­ятность безотказной работы, плотность вероятности f (t)и интен­сивность отказов ЭА за время t = 150 ч. Вычислить среднюю нара­ботку до первого отказа.

Задача 40. Время исправной работы элемента ЭА подчинено гамма-распределению с параметрами a = 2,6, θ = 0,610⁷. Необхо­димо определить вероятность безотказной работы, плотность ве­роятности f (t), интенсивность отказов элемента за 10 000 ч, 5000 ч. Вычислить среднюю наработку до первого отказа элемента.

Задача 41. Интенсивность отказов схемы управления ЭА од­ной из подсистем самолета λ = 0,82-10^-3 1/ч = const. Необходимо найти вероятность безотказной работы в течение 6 ч полета само­лета, плотность вероятности f (t)при t = 100 ч и среднюю наработ­ку до первого отказа.

Задача 42. Определить, какова должна быть средняя наработ­ка до отказа ЭА, имеющего экспоненциальное распределение на­работки до отказа, чтобы вероятность безотказной работы была не менее 0,99 в течение наработки t = 300 ч.

Задача 43. Время безотказной работы блока ЭА подчинено усе­ченному нормальному закону с параметрами т = 8000 ч, σ = 2000 ч. Определить вероятность безотказной работы блока для значений наработки 4000, 6000, 8000, 10 000 ч.

Задача 44. Определить, какова должна быть средняя наработ­ка до отказа ЭА, имеющего усеченное нормальное распределение наработки до отказа, чтобы вероятность безотказной работы была не менее 0,98 в течение наработки t = 500 ч для σ = 200 ч.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Какова зависимость между вероятностью безотказной работы объ­екта и его средней наработкой до отказа?

2. Как связаны между собой вероятность безотказной работы и интен­сивность отказов объекта?

3. Объясните связь вероятности безотказной работы, интенсивности от­казов и средней наработки до отказа объекта.

4. Каким образом выглядит соотношение между плотностью распреде­ления и интенсивностью отказов при экспоненциальном законе на­работки объекта до отказа?

5. Выведите уравнение, связывающее параметр потоков отказов объ­екта и плотность распределения наработки до отказа.

6. Покажите, как аналитически связана вероятность и интенсивность восстановления объекта.

7. Дайте определение понятиям «случайная величина» и «вероятность», исходя из понятия «вероятностное пространство».

8. Какие вы знаете характеристики случайных величин?

9. Перечислите известные вам моменты случайных величин.

10. В чем особенности формулы Байеса?

11. Какой смысл имеет центральная предельная теорема?

12. Напишите формулу биномиального закона распределения случай­ных величин и закона Пуассона.

13. Какова роль нормального (гауссовского) закона распределения в тео­рии надежности?

14. В каких случаях применяется экспоненциальное распределение в за­дачах надежности?

15. С какой целью используется в теории надежности композиция зако­нов распределения?

16. В чем заключаются особенности многомерных распределений слу­чайных величин?

17. Каковы отличия усеченного нормального распределения?

18. Какова вероятность безотказной работы объекта в течение средней наработки до отказа, если аналитическое выражение интенсивности отказов имеет вид λ(t) = at?

Примечание:

19. Какова вероятность безотказной работы объекта в течение средней наработки до отказа, если плотность распределения наработки до отказа имеет вид

20. Вычислите математическое ожидание и дисперсию наработки до от­каза для экспоненциального закона.

21. Плотность распределения наработки до отказа системы контроля имеет вид

Необходимо получить аналитические выражения для всех количественных показателей надежности, а именно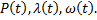

22. Доказать, что при плотности распределения наработки до отказа вида
существует установившееся значе­ние интенсивности отказов, равное меньшему из значений и

23. Доказать, что если плотность распределения между отказами имеет вид и отказы независимы, то уста­новившееся значение параметра потока отказов всегда больше уста­новившегося значения интенсивности отказов.

24. Плотность распределения наработки до отказа технических объек­тов может иметь вид:

а)

б)

Необходимо получить аналитические выражения для вычисления таких показателей надежности, как вероятность безотказной рабо­ты, интенсивность отказов, средняя наработка до отказа, параметр потока отказов.

25. Анализ данных об отказах устройства управления (УУ) показал, что
вероятность его безотказной работы выражается формулой

Вычислить среднюю наработку до отказа УУ, если известно, что λ= 10³. Вычислить вероятность безотказной работы, значение ин­тенсивности отказов, плотность распределения наработки до отка­зов при t = 1000 ч работы УУ.

25. Интенсивность отказов объектов управления зависит от времени и
выражается функциями:

a)

b)

Требуется определить показатели надежности

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: