Непрерывные распределения случайных величин в теории надежности

Рассмотрим закон равномерного распределения непрерывных и дискретных случайных величин.

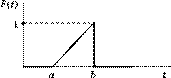
Пусть интенсивность отказов ЭА и оборудования в интервале (a, b). Из свойств функции распределения вытекает Поэтому плотность равномерного распределения задается формулой

При значении и функция f(t) терпит разрыв

(рис. 4.6).

Рис. 4.6 Закон равномерного распределения функции F(t)

Если то

Для

Если то

 

Таким образом, закон равномерного распределения задается формулой

Рис. 4.7 Закон распределения функции F(t)

Графически он отображается рис. 4.7. Эта функция не прерывна повсюду.

Нормальное (гауссовское) распределение. Случайная величи­на, значения которой зависят от суммарного воздействия числа различных факторов, каждый из которых, взятый в отдельности, влияет на величину сравнительно мало, будет подчиняться нор­мальному закону распределения. Для этого закона плотность ве­роятности ϕ(t) задается формулой

Вид плотности нормального распределения:

где Р = 0,4769 является решением уравнения

определяется из соотношения

и называется срединным (или вероятностным) отклонением.

 

 

Таблица 4.3 – Непрерывное распределение случайных величин, используемых в задачах теории надежности

 

 

Фундаментальная роль, которую играет нормальное распреде­ление, объясняется тем, что при широких предположениях сум­мы случайных величин с ростом числа слагаемых ведут себя асим­птотически нормально.

С помощью линейного преобразования нормаль­ное распределение с произвольными параметрами приводит­ся к нормальному распределению с параметрами

(0, 1), называе­мому стандартным нормальным распределением с функцией рас­пределения

Как правило, табулируется функция

связанная с Ф(х) соотношением Ф(х) = 0,5 + Ф₀(х).

Нормально распределенная случайная величина с большой ве­роятностью принимает значения, близкие к своему математиче­скому ожиданию, что выражается правилом сигм:

Чаще всего используется правило трех сигм.

Нормальное распределение безгранично делимо: если сумма двух независимых случайных величин имеет нормальное распре­деление, то и каждое распределение имеет нормальное распреде­ление.

Вероятность попадания нормальной случайной величины ξ, в интервал [ а, β] составляет

(4.56)

После замены переменной х на вычисление интеграла в (4.56) сводится к вычислению соотношения

(4.57)

где

При преобразованиях выражений, содержащих функцию Ла­пласа Ф(х), можно пользоваться следующими свойствами этой функции:

Нормальное распределение вероятностей n-мерного случайно­го вектора описывается формулой

(4.58)

где математических ожиданий; корреляцион­ная матрица; определитель корреляционной матрицы.

Если случайная ξ имеет конечные моменты до четвертого вклю­чительно, то величина

называется коэффициентом асимметрии, а

— коэффициентом эксцесса ее распределения.

Указанные величины характеризуют степень отличия функ­ции распределения 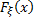от функции распределения Ф(х) стандарт­ного нормального распределения, для которого коэффициенты асимметрии и эксцесса равны нулю, а мода и медиана совпадают с математическим ожиданием.

Непрерывным аналогом геометрического распределения слу­чайной величины ξ, является показательное (экспоненциальное) распределение с параметром λ > 0. Экспоненциальное распределе­ние применяется для описания процессов, обладающих свойством отсутствия последействия:

В связи с этим экспоненциальное распределение является ос­новным в теории стационарных марковских процессов и широко распространено в теории надежности и массового обслуживания.

Экспоненциальное распределение — один из основных зако­нов распределения наработки объектов. Так как

то при X (t) — const

Рассмотрим простейший поток событий, например безотказ­ность выключателя, которая зависит от ожидаемой интенсивно­сти коммутации и начального ресурса к моменту включения в ра­боту. При условии, что интенсивность отказов λ (t) — λ = const, без­отказность работы будет соответствовать

Таким образом, экспоненциальное распределение является однопараметрическим распределением с параметром, представляющим постоянную интенсивность отказов. Верно и обратное утверждение: если λ(t) = const, то ВБР как функция времени подчиняется экспоненциальному закону. При

(рис. 4.8)

Дисперсия времени безотказной работы для экспоненциального распределения

Следовательно, коэффициент вариации

Экспоненциальный закон хорошо описывает распределение времени безотказной работы объектов при внезапных отказах, рас­пределение времени между соседними отказами и времени восста­новления. Для объектов, у которых явно выражены при эксплуа­тации явления износа и старения, применение экспоненциально­го закона недопустимо.

Промежутки времени между событиями простейшего потока чаще всего независимы. Простейший поток называется потоком с ограниченным последствием или потоком Пальма. Его примером может служить непрерывная работа предохранителей до перего­рания плавкой вставки. После замены новой или установки ново го предохранителя начинается новый интервал безотказной рабо­ты. В этом случае отдельные предохранители выходят из строя независимо друг от друга.

Пример 3. В течение семи часов рабочей смены в распредели­тельном устройстве произошло два коротких замыкания, в резуль­тате чего выключатель отключался. Определить вероятность того, что в течение восьмого часа произойдет еще одно отключение ап­парата.

Гамма-распределение является аналогом дискретного отри­цательного биномиального распределения (распределения Паска­ля). При а = 1 гамма-распределение совпадает с показательным, а при а = 0,5 n и λ = 0,5 — с распределением с п степенями свобо­ды. При и а = п гамма-распределение называется распреде­лением Эрланга с параметрами (п, μ) и описывает распределение длительности интервала времени до появления п событий процес­са Пуассона с параметром μ. Распределение Эрланга используется в теории массового обслуживания и теории надежности. Если эрланговское распределение стремится к вырожденному (другому виду распределения). При 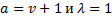гамма-рас­пределение называют показательно-степенным распределением с параметром т, функция распределения которого имеет вид

Распределение Вейбулла — Гнеденко с параметрами а, λ, (а, λ > 0) описывает предельное распределение максимума. Пусть слу­чайные величины 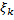взаимно независимы и одинаково распреде­лены и для . Положим 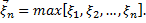Для того чтобы при выборе некоторых констант распределения случайных величин сходились к распределению не сосредо­точенному в 0, необходимо и достаточно, чтобы функция

была правильно меняющейся с показателем а (а < 0). В этом слу­чае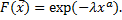

Распределение Вейбулла — Гнеденко широко применяется в теории надежности для описания времени безотказной работы объ­ектов, в частности хорошо моделирует распределение отказов ЭА низкого напряжения, а именно коммутационных ЭА.

Согласно этому распределению плотность вероятности време­ни безотказной работы

(4.59)

где а — параметр, определяющий форму (асимметрию и эксцесс) распределения; θ — параметр, определяющий масштаб распреде­ления (λ = 1/θ).

Вероятность безотказной работы

и средняя наработка до отказа

где Г(х)— полная гамма-функция.

При а = 1 рассматриваемое распределение превращается в экс­поненциальное с параметром

λ = 1/θ, θ = Т_СР.

Двухпараметрическое распределение Вейбулла — Гнеденко мо­жет быть использовано при анализе надежности объектов как в период приработки, так и на нормальном этапе эксплуатации объ­ектов.

Широкое распространение в теории вероятностей и математи­ческой статистике получило -распределение. Пусть — независимые случайные величины, имеющие стандартное нормальное распределение. Случайная величина

имеет χ²-распределение с n степенями свободы.

Если — n -мерный нормальный векторе мате­матическим ожиданием

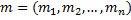и невырожденной ко­вариационной матрицей то случайная величина

имеет χ²-распределение с п степенями свободы; индекс «Т» озна­чает операцию транспонирования; — элементы матрицы . На изучении χ²-статики Пирсона

основан один из критериев проверки согласия эмпирических дан­ных с гипотетической функцией распределения F { x }. Вероятность

п, — число наблюдений, попавших в полуинтер­вал

Если — независимые случайные величины, имею­щие стандартное нормальное распределение, то

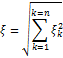
имеет χ-распределение с n степенями свободы. При п = 2 χ-распределение называется распределением Рэлея (Рэлея — Раиса), а при п = 3 — распределением Максвелла.

Для распределения Рэлея основные характеристики наработ­ки объекта имеют следующий вид:

 

(4.60)

где σ — параметр распределения Рэлея.

Распределение Рэлея можно получить из распределения Вейбулла, приравняв а = 2.

Пусть η и ϛ— независимые случайные величины, причем η имеет нормальное стандартное распределение, а ϛ χ²-распределение с n степенями свободы, тогда 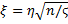, имеет распределение Стьюдента (t-распределение) с n степенями свободы. При а = 1 рас­пределение Стьюдента совпадает с распределением Коши с пара­метрами а, λ(λ > 0).

Если случайная величина η имеет нормальное (0, 1) распреде­ление, то имеет логарифмически нормальное (логнормальное) распределение. Его можно получить как частный слу­чай распределения Кептейна, имеющего плотность вероятности

(4.61)

где G(x) — монотонная дифференцируемая функция.

Распределение Парето с параметрами х₀, а (а > 0, х₀ > 0) есть усечение на интервале

степенного распределения с пара­метром а, имеющего плотность вероятности

В математической статистике при сглаживании распределений эмпирических данных широко используются распределения Пир­сона, плотности вероятности которых являются решениями диф­ференциального уравнения

где — параметры распределения.

Распределения Пирсона полностью определяются первыми че­тырьмя моментами. Пусть — k- йцентральный момент случайной величины, имеющей распределение Пирсона. Тогда если

, то

(4.62)

где

Для определения распределения Пирсона, аппроксимирующе­го данные наблюдений, вычисляют первые четыре момента и из (4.62) находят оценки параметров.

В соответствии с распределением корней квадратного трехчле­на различают 12 типов распределений Пирсона. В за­висимости от значений параметров распределения отдельные типы распределений Пирсона совпадают с другими видами распределе­ний. Так, распределения Пирсона типа I являются β-распределениями, типа III — гамма-распределениями, типа VII — распреде­лениями Стьюдента, типа X — показательными распределениями, типа XI — нормальными распределениями.

Равномерное распределение является аналогом распределений классической теории вероятностей, описывающих случайные экс­перименты с равновероятными сходами. Если случайная величи­на ξ, имеет непрерывную функцию распределения то случай­ная величина имеет равномерное распределение на отрез­ке [0, 1]. Этим объясняется широкое использование равномерного распределения в статистическом моделировании (методы Монте-Карло). Если случайная величина ξ, имеет равномерное распреде­ление на отрезке [ а, b](а < b), то случайная величина с помощью линейного преобразования приводится к равно­мерному распределению на отрезке [0, 1]. Равномерным распре­делением на отрезке [-0,5, 0,5] удовлетворительно описывается погрешность, происходящая от округления числа.

Усеченное нормальное распределение. Нормальное распреде­ление (закон распределения Гаусса) занимает особое место и игра­ет исключительно важную роль в теории вероятностей и теории надежности. Основная его особенность состоит в том, что оно яв­ляется предельным, к которому при стремлении к бесконечности числа испытаний приближаются другие распределения. Можно показать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, из которых каждая в от­дельности сравнительно мало влияет на общую сумму, приближен­но подчиняется нормальному закону. В отличие от экспоненци­ального, вейбулловского и других распределений, которые при­менимы только для положительных непрерывных случайных величин, нормальное распределение употребляется для непрерыв­ных случайных величин, которые могут принимать как положи­тельные, так и отрицательные значения от . Плотность вероятности для нормального распределения имеет вид

(4.63)

где т_х — математическое ожидание; σ_х — среднее квадратическое отклонение случайной величины х

Этот очевидный недостаток рассмотренной модели для описа­ния времени безотказной работы становится несущественным, если (практически, если ). Поэтому количествен­ные характеристики надежности имеет смысл рассматривать толь­ко при усеченном нормальном законе, отсекая часть кривой рас­пределения при t < 0 и вводя нормирующий множитель С для того, чтобы сохранить условие нормирования плотности вероятности

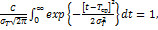(4.63)

где

(4.65)

Ф(x) – интеграл Лапласа,

Усеченный нормальный закон распределения применяется для описания постепенных отказов объектов, что характерно для «ста­реющих» объектов.

Композиция законов распределения. У сложных объектов за­коны распределения времени безотказной работы являются соче­танием многих разнообразных распределений, присущих отдель­ным элементам. Поэтому в зависимости от превалирующего влия­ния на отказ объекта того или иного элемента мы можем получать различные законы распределения объекта в целом.

Допустим, что имеется несколько случайных величин X, Y, Z с плотностями распределения вероятностей f (x), f (y), f (z). Закон распределения случайной величины U = X + Y + Z называется ком­позицией законов распределения величин X, Y, Z. Плотность рас­пределения f (u)является композицией распределений f (x), f (y), f (z). Композиция может существовать для любого числа случай­ных величин.

Композиции законов распределения имеют ряд общих и част­ных свойств. Общие свойства не зависят от вида рассматриваемых законов распределения, а частные применимы только к опреде­ленным законам распределения.

Общие свойства композиции законов распределения:

1. Математическое ожидание композиции распределения рав­но сумме математических ожиданий независимых случайных ве­личин, образующих рассматриваемую сложную случайную вели­чину:

М (и) = М (х) + М (у) + M (z) +...

2. Дисперсия композиции распределения равна сумме диспер­сий независимых случайных величин, составляющих данную слож­ную случайную величину:

D (u)= D (x) + D (y) + D (z) +...

При значительной разнице дисперсий составляющих незави­симых случайных величин дисперсия композиции будет близка к дисперсии той случайной величины, у которой она имеет наиболь­шие значения.

Частные свойства композиции законов распределения:

1. Композиция распределений Пуассона дает также распреде­ление Пуассона (справедливо для любого числа распределений).

2. Композиция случайных величин с нормальным распределе­нием есть также нормальное распределение.

Из всех распределений, применяемых в теории надежности, только эти два распределения обладают таким свойством, что их композиция дает снова то же распределение.

3. Композиция экспоненциальных распределений дает новое гамма-распределение.

Если взять большое число любых распределений (с одинако­выми или различными законами распределения) при условии, что дисперсии составляющих распределений не сильно отличаются друг от друга, то их композиции будут близки к нормальному.

4.6.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: