 |
Примеры решения типовых задач при расчете надежности резервированных
|
|
|
|
ВОССТАНАВЛИВАЕМЫХ СИСТЕМ, ОСНОВАННОМ НА СОСТАВЛЕНИИ ГРАФА ПЕРЕХОДОВ СИСТЕМЫ ИЗ ОДНОГО СОСТОЯНИЯ В ДРУГОЕ
Изучение вероятностных процессов занимает большое место в анализе и обеспечении надежности сложных объектов, так как их функционирование представляет собой реализацию вероятностных процессов. Вероятностным (или случайным) процессом называется случайная функция, аргументом которой является время. Чтобы охарактеризовать вероятностный процесс, необходимо указать тип процесса и его числовые характеристики. Существует большое число различных типов вероятностных процессов. Поскольку функционирование сложных объектов, как правило, сопровождается простейшими потоками отказов и восстановлений (простейшим называется поток, обладающий свойством ординарности, стационарности и отсутствием последействия), наиболее подходящим для описания таких процессов является марковский процесс. Кроме того, время работы до отказа и время восстановления имеют экспоненциальное распределение.
Марковский процесс — это процесс, у которого для каждого момента времени вероятность любого состояния системы в будущем зависит только от ее состояния в настоящий момент времени и не зависит от того, каким образом система пришла в это состояние. Характеристику процесса удобно сопровождать графическим изображением (графом состояний и переходов). С его помощью изображаются процессы перехода системы из одного состояния в другое в случайные моменты времени. Граф переходов может быть представлен либо матрицей переходов, либо системой уравнений.
Задача 30. Провести расчет надежности объекта, если он может находиться в двух состояниях: работоспособном и отказа. Интенсивность перехода в состояние отказа равна λ, в работоспособное — μ.
|
|
|
Решение.
1. Составим граф переходов, как показано на рис. 7.33.
2. Запишем систему дифференциальных уравнений:
3. Произведем переход к изображениям Лапласа (табл. 7.2) и определим P1 (z):
Вероятности Pt(t)определялись из начальных условий: в момент включения все элементы исправны, т. е.
Для приведения выражения Po(z)к табличному умножим и разделим правую часть на постоянную величину, равную (λ+ μ). В результате получим
Таблица 7.2
Переход от функции оригинала к функции изображения
ЗАДАЧИ И УПРАЖНЕНИЯ ПО РАСЧЕТУ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ
РЕЗЕРВИРОВАННЫХ СИСТЕМ, ОСНОВАННОМУ НА СОСТАВЛЕНИИ
ГРАФА ПЕРЕХОДОВ
Задача 31. Для питания радиостанции используется электроагрегат с двумя генераторами, производительность каждого из которых достаточна для нормальной работы; генераторы работают поочередно. При отказе работающего генератора (или соответствующих устройств регулирования и коммутации) в работу включается резервный генератор, а отказавший отключается и ремонтируется. Отказ электроагрегата состоит в прекращении питания радиостанции. Конструкция электроагрегата допускает одновременный ремонт обоих генераторов, имеется нужное число ремонтников. Вычислить коэффициент готовности электроагрегата, если наработка на отказ т 1генератора в 5 раз больше среднего времени устранения отказа тτ. Предположить показательное распределение времени безотказной работы и времени восстановления.
Задача 32. Электрический аппарат, состоящий из рабочего блока и блока в нагруженном резерве, рассчитан на непрерывную круглосуточную работу. Через три часа после включения ЭА может получить команду на перестройку режима работы. Интенсивность отказов и восстановления каждого блока равны 
и μ = 0,2 1/ч. Имеются две дежурные ремонтные бригады. Определить вероятность застать ЭА в неработоспособном состоянии через три часа после включения.
|
|
|
Задача 33. ЭА включает силовой и защитный блоки, интенсивности отказов которых одинаковы и равны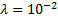 
1/ч. Интенсивность восстановления μ = 2 1/ч. ЭА обслуживает одна ремонтная бригада. При неработоспособности любого из блоков ЭА неработоспособен. При этом работоспособный блок не включается и в нем могут произойти отказы. Требуется определить значения коэффициентов готовности и простоя ЭА.
Задача 34. В отличие от задачи 33 при неработоспособности любого блока второй работоспособный блок выключается, и в нем не могут происходить отказы.
Задача 35. Отличие от задачи 34 в том, что помимо работающих имеются приемный и передающий блоки в нагруженном резерве. Применено общее активное резервирование ЭА, переключающее устройство предполагается абсолютно надежным.
Задача 36. Требуется рассчитать надежность устройства, схема которого изображена на рис. 1.6. Вероятность безотказного состояния каждого из элементов за 100 ч равна 0,9. Определить вероятность безотказной работы устройства за 100 ч.
Задача 37. Рассчитать вероятность безотказной работы системы, структурно-функциональная схема которой представлена на рис. 7.34. Предположим, что восстановление начинается сразу после отказа элемента и восстанавливаться могут сразу несколько элементов.
Задача 38. Длительность безотказной работы каждого из двух устройств и суммарная длительность их восстановления подчиняются экспоненциальному закону с параметрами λ и μ соответственно. Необходимо определить функцию готовности дублированной системы с ненагруженным резервом, восстанавливаемой после отказа основного и резервного устройства.
Задача 39. Основным ненадежным элементом непрерывно работающего ЭА является расцепитель. Восстановление ЭА заключается в простой замене расцепителя из числа имеющихся т запасных. Время работы до отказа и время замены расцепителя распределено по экспоненциальному закону с параметрами λ и μ соответственно. Требуется найти вероятность застать ЭА в момент t в исправном состоянии. Исследовать поведение этой вероятности при 
|
|
|
Задача 40. Имеется непрерывно работающая двухканальная линия передачи электроэнергии. Восстановление отказавшего канала требует выключения всей линии. Доля мощности, не доставляемой потребителям в единицу времени при простое r каналов (r = 1,2), равна Wr. Время безотказной работы и время восстановления канала имеют экспоненциальное распределение с параметрами λ и μ соответственно. Требуется найти, при каком количестве r отказавших каналов остановка линии на восстановление будет обеспечивать минимум потерь передаваемой мощности. При остановке линии после отказов обоих каналов рассмотреть следующие случаи (рис. 7.35):
а) каналы восстанавливаются поочередно;
б) одновременно могут восстанавливаться два канала.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Дайте определение понятию «резервирование».
2. Что такое избыточность?
3. Какие вы знаете признаки классификации методов резервирования?
4. Раскройте содержание структурного резервирования.
5. Расскажите о временном и информационном резервировании объекта.
6. В чем особенности функционального резервирования объектов?
7. Как классифицируются объекты по способу соединения резервных элементов?
8. Перечислите и дайте краткую характеристику способам включения резерва в объектах.
9. Чем характеризуется степень избыточности в методах резервирования объектов?
10. В каких режимах могут работать резервные элементы в объектах?
11. Выведите основные соотношения надежности для общего резервирования объекта.
12. Расскажите о последовательности расчета надежности объекта с раздельным резервированием элементов.
13. Как оценивается выигрыш надежности при резервировании объектов?
14. В чем особенности расчета надежности объекта при резервировании с дробной краткостью?
15. Каковы принципы мажоритарного резервирования объектов?
16. Объясните, как вы понимаете сущность логико-вероятностных методов расчета надежности систем.
17. Раскройте алгоритм расчета надежности с помощью логико-вероятностного метода для систем, имеющих параллельную структуру.
|
|
|
18. Выведите уравнение для расчета надежности восстанавливаемого резервированного объекта с использованием графа переходов его состояний.
19. Какими способами можно решать уравнения, описывающие вероятности состояний резервированной системы с восстановлением?
20. Что такое «стационарный коэффициент готовности системы»?
21. Как учитывается последействие отказов при расчете надежности резервированных объектов?
|
|
|
