 |
Уравнения Лагранжа первого рода
|
|
|
|
Воспользуемся условием (3.3) для выражения реакций идеальных голономных связей. Перепишем (3.3) в виде
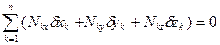, (3.5)
учтем, что возможные перемещения, обусловленные изменением декартовых координат (в соответствии с (1.4)), подчинены уравнениям
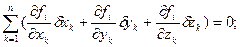
(3.6)
Каждое из этих уравнений умножим на соответствующий неопределенный множитель Лагранжа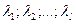 
, зависящий, в общем случае, от координат и времени:
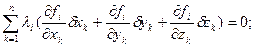
Полученные выражения сложим
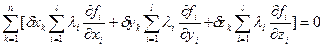. (3.7)
Вычтем (3.7) из (3.5):
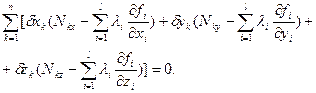(3.8)
Выберем неопределенные множители Лагранжа 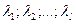таким образом, чтобы коэффициенты при возможных перемещениях по 
координатам (выражения в круглых скобках) обращались в нуль. Оставшиеся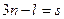 
возможных перемещения независимы (так как 
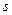- число степеней свободы механической системы), поэтому множители при них также должны быть равны нулю. Тогда
; 
; 
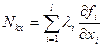. (3.9)
Дифференциальные уравнения движения точек механической системы в проекциях на оси декартовой координатной системы имеют вид
;
; 
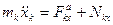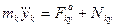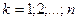
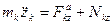; (3.10)
где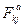 
- проекция на 
- ю ось равнодействующей активных сил, приложенных к 
-ой точке, а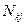 
- равнодействующая реакций идеальных связей, записанная через множители Лагранжа по формулам (3.9). В таком случае уравнения (3.10) примут вид:
;
;
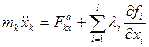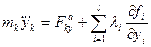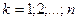
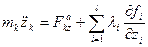. (3.11)
Система уравнений (3.11) называется уравнениями Лагранжа первого рода.
Присоединив к системе из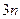 
дифференциальных уравнений (3.11) уравнений голономных связей
; 
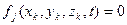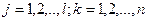(3.12)
будем иметь систему из 
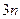уравнений для определения неизвестных функций координат 
и множителей Лагранжа 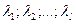. После решения полученной системы уравнений проекции реакций на координатные оси могут быть найдены по формулам (3.9).
В том случае, если на механическую систему наложены идеальные линейные неголономные связи, т.е. связи, в уравнения которых проекции скоростей входят линейно, последовательность действий по составлению соответствующих уравнений Лагранжа первого рода остается прежней.
|
|
|
Уравнения таких связей имеют вид
; 
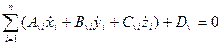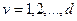(3.13а)
или
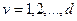; (3.13б)
где 
- число неголономных связей; 
- функции координат и времени, если связи нестационарные. Если 
, то связи называются однородными линейными неголономными.
Пусть на механическую систему наложено голономных связей
и неголономных связей вида (3.12). Тогда возможные перемещения в декартовых координатах должны удовлетворять следующим уравнениям:
; 
(3.14)
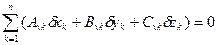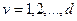; (3.15)
Следовательно, если эти 
уравнений независимы, то число степеней свободы механической системы (а так же число независимых возможных перемещений) равно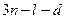 
.
Первые из этих уравнений умножим на соответствующий неопределенный множитель Лагранжа 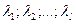, а вторые – на соответствующий неопределенный множитель Лагранжа 
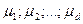, зависящие, в общем случае, от координат и времени. Выполнив ряд действий, оговоренных выше, получим обобщение формулы (3.11):
;
;
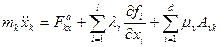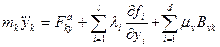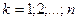
. (3.16)
Присоединив к системе из 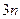дифференциальных уравнений (3.16) уравнений голономных связей (3.14) и уравнений линейных неголономных связей (3.15), будем иметь систему из 
уравнений для определения 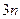неизвестных функций координат и множителей Лагранжа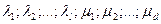 
.
ПРИМЕР 3.2. (пример из параграфа 3 [3]). Две весомые материальные точк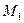и 
и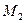 
с одинаковыми массами 
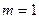соединены жестким стержнем длины пренебрежимо малой массы. Система может двигаться только в вертикальной плоскости и только так, что скорость середины стержня направлена вдоль стержня. Определить движение точек 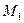и .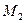
РЕШЕНИЕ. В качестве обобщенных координат выберем декартовы координаты точек 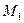и 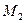. Запишем для них уравнения связей:
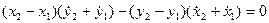. (3.17)
Уравнения Лагранжа с неопределенными множителями 
и 
имеют вид
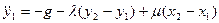(3.18)
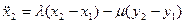
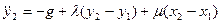(3.19)
Из (3.18) с учетом первого уравнения (3.17), определим и :
|
|
|
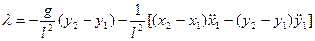
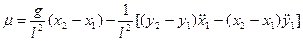(3.20)
Заметим, что уравнения (3.19) получаются из уравнений (3.18), если заменить на 
и 
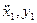на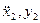 
. Поэтому, определяя и из уравнений (3.19), находим:
(3.21)
Приравняв между собой соответствующие выражения для и в формулах (3.20) и (3.21), после элементарных преобразований получим:
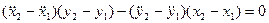
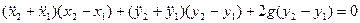(3.22)
Введем сокращенные обозначения:
(3.23)
Тогда уравнения (3.17) и (3.22) перепишутся так:
; 
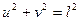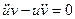(3.24)
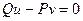(3.25)
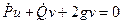(3.26)
Равенства (3.24) показывают, что в плоскости (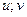
) точка с координатами 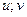движется по окружности радиуса с центром в начале координат, причем ее ускорение все время направлено к центру окружности. Но тогда движение этой точки будет равномерным. Поэтому
; 
; 
; 
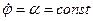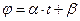. (3.27)
Согласно равенству (3.25) можно положить
; 
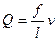. (3.28)
Подставляя эти выражения в равенство (3.26) и учитывая равенства (3.24) и (3.27), найдем:
; т.е. 
.
Тогда
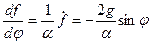и 
.
Следовательно, в силу равенств (3.27) и (3.28), имеем:
; 
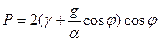. (3.29)
Интегрируя, найдем
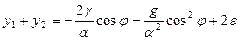(3.30)
Из равенств (3.23), (3.27) и (3.30) окончательно получим:
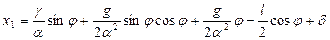
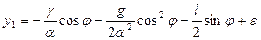
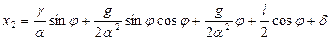(3.31)
(
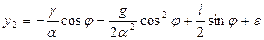
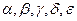- произвольные постоянные).
Вопросы и задачи для самоконтроля
1. Сформулируйте принцип Даламбера для материальной точки.
2. Сформулируйте метод кинетостатики для механической системы?
3. Запишите общее уравнение динамики для механической системы. Сколько таких независимых уравнений можно записать для механической системы с 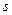степенями свободы, если на систему наложены геометрические связи?
4. Запишите общее уравнение динамики для механической системы с идеальными геометрическими связями.
5. Для механических систем с какими типами связей справедливы уравнения (3.11)?
6. Возможно ли составление уравнений Лагранжа первого рода для механической системы с неголономными связями? Если это возможно, как должны выглядеть уравнения таких связей?
|
|
|
