 |
Особенности применения уравнений Лагранжа второго рода для систем с неудерживающими связями
|
|
|
|
Ели связи, наложенные на механическую систему неудерживающие, может иметь место ситуация, когда связь в некоторый момент перестает действовать (либо наоборот – накладывается). Силовые схемы на этапах движения с действующей связью и без нее, различны и, как следствие, различны на этих этапах дифференциальные уравнения, описывающие движение механической системы. Характерным примером является спуск с горы лыжника, который может оторваться от поверхности горы вследствие резкого изменения ее профиля (трамплин) либо достаточно высокой скорости на выпуклости. В последнем случае точка отрыва от связи (начало этапа полета) определяется равенством нулю силы нормального давления лыжника. Конечные положение и скорость на этапе скольжения есть начальные положение и скорость для этапа полета.
Точкой окончания этапа полета является точка пересечения траектории полета и профиля поверхности горы. Если в этой точке касательные к траектории движения и к профилю поверхности окажутся достаточно близкими, лыжник приземлится «мягко» (иногда говорят, что он хорошо «вписался»), если нет – будет иметь место механический удар.
Таким образом, решение задачи о движении механической системы с неудерживающими связями может представлять собой ряд этапов, для каждого из которых составляется своя силовая схема и выводятся свои дифференциальные уравнения; при этом конечные кинематические характеристики предыдущего этапа являются начальными для последующего. На протяжении рассматриваемого этапа осуществляется контроль величины параметра, определяющего переход к следующему этапу движения, на котором либо какие–то связи прекращают действовать либо начинают действовать дополнительные связи. Сказанное проиллюстрируем примером.
|
|
|
ПРИМЕР 4.6 (пример из [2], п.19.4). Стержень АВ скользит без трения по сторонам прямого угла (рис. 4.6).
До тех пор, пока стержень опирается на стороны угла, связи не нарушены и уравнение движения стержня может быть получено из уравнения движения линейки эллипсографа при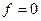 
, т.е.
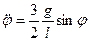. Это уравнение может быть представлено в виде
и проинтегрировано при начальных условиях 
, 
(движение наклоненного стержня из состояния покоя).
Тогда первый интеграл будет 
.
Однако сразу использовать эти уравнения нельзя, так как не известно, произойдет или нет отрыв стержня от вертикальной стенки. Если отрыв может иметь место, то надо определить угол 
, соответствующий этому моменту. Очевидно, что сила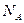 
нормального давления на стену в момент отрыва должна стать равной нулю, то есть
.
Выразим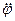 
и 
из дифференциального уравнения движения и его первого интеграла и подставим в выражение для силы нормального давления. Тогда
,
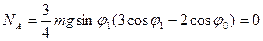Отсюда 
. Таким образом, полученное уравнение Лагранжа определяет движение не при всех 
, как это было в случае удерживающих связей, а только если 
.
С момента отрыва точки А от вертикальной стены стержень будет иметь не одну, а две степени свободы (по предположению движение происходит в вертикальной плоскости). Если нас интересует дальнейшее движение стержня, то, как уже говорилось выше, для второго этапа движения следует изобразить стержень АВ с действующими на него силами (см. рис.4.6 при отсутствии реакции 
), получить каким-либо методом дифференциальные уравнения движения стержня и проинтегрировать их. При этом начальными условиями для второго этапа будут найденный угол , при котором происходит отрыв точки А стержня от вертикальной стены, и угловая скорость 
, которой обладал стержень в этот момент времени.
Следует отметить, что единообразие в составлении уравнений Лагранжа, с одной стороны являясь его достоинством, с другой стороны не позволяет, в некоторых случаях, произвести анализ действия сил, и, как следствие, поведения механической системы, что для инженера оказывается серьезным недостатком. Избежать этого позволяет комбинирование уравнений Лагранжа с общими теоремами механики (как это было сделано выше).
|
|
|
4.6. Уравнения движения для неголономных систем с множителями Лагранжа *
В настоящем пособии ограничимся рассмотрением механических систем с линейными неголономными связями, т.е. со связями, в уравнения которых проекции скоростей входят линейно. Уравнения таких связей имеют вид
; 
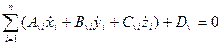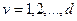(4.10а)
или
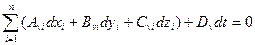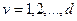; (4.10б)
где 
- число неголономных связей; 
- функции координат и времени, если связи нестационарные. Если 
, то связи называются однородными линейными неголономными.
Пусть на механическую систему наложено 
голономных связей
; 
(4.11)
и неголономных связей вида (4.10). Тогда возможные перемещения в декартовых координатах должны удовлетворять следующим уравнениям:
; (4.12)
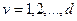; (4.13)
Следовательно, если эти 
уравнений независимы, то число степеней свободы механической системы (а так же число независимых возможных перемещений) равно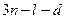 
.
Заметим, что всякая геометрическая связь, если ее уравнение продифференцировать по времени, станет кинематической (но интегрируемой). Напомним, что неинтегрируемая кинематическая связь (неголономная), накладывая ограничения на скорости, в явном виде не влияет на независимость выбранных обобщенных координат.
ПРИМЕР 4.7 (пример 53 из [1]). Пусть тело А перемещается по неподвижной плоскости, касаясь ее в трех точках (рис.4.7).
Предположим, что одна из точек касания М является точкой касания острого конька поверхности плоскости и может перемещаться только вдоль плоскости конька, движение же двух других точек по плоскости пусть будет свободным (так как положение этих точек несущественно, то на рисунке они и не показаны).
РЕШЕНИЕ. Поскольку тело А совершает плоское движение, его положение может быть определено координатами точки 
и углом , образованным плоскостью конька с осью 
. Условие отсутствия проскальзывания конька в поперечном направлении может быть записано в виде 
, или, что то же самое, 
.
|
|
|
Итак, из-за наличия неголономной связи число степеней свободы для тела А будет (3 – 1) = 2. При этом изменения обобщенных координат 
не могут быть произвольными, хотя в силу неинтегрируемости уравнения связи все эти координаты остаются независимыми.
Пусть 
будут независимыми обобщенными координатами механической системы с неголономными связями; записав уравнения (4.10) через обобщенные координаты, получим выражений вида
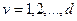; (4.14)
В предыдущем параграфе был рассмотрен прием составления уравнений Лагранжа второго рода для случая, когда на механическую систему наложены дополнительные связи. Так как вводимые связи идеальные, то
(4.15)
где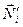 
- реакции неголономных связей, 
- обобщенные силы, соответствующие этим реакциям. Формулу (4.14) можно записать в ином виде (см. (4.10а и 4.13)):
; .
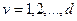Умножим каждое из этих соотношений на соответствующий множитель Лагранжа 
и сложим полученные соотношения между собой:
. (4.16)
Вычитая из выражения (4.15) соотношение (4.16), получим
.
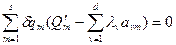Число независимых возможных перемещений равно числу степеней свободы механической системы 
. В силу этой независимости должны быть равны нулю 
коэффициентов перед возможными перемещениями (выражения в скобках). Выберем 
так, чтобы выражения в круглых скобках перед остальными возможными перемещениями обращались в нуль; тогда
, 
(4.17)
и, следовательно, уравнения движения при наличии неголономных связей будут иметь вид
, . (4.18)
Уравнения (4.18) вместе с уравнениями связей (4.14) образуют замкнутую систему из (
) уравнений относительно неизвестных (
.
ПРИМЕР 4.8. Пусть в примере 4.7 проекция центра масс С тела А на плоскость 
совпадает с точкой М касания конька. Рассмотрим движение этого тела под действием заданной силы 
, приложенной в центре масс и направленной вдоль конька, а так же заданного момента 
(см. рис.4.8).
РЕШЕНИЕ. Кинетическая энергия тела равна
; где 
– масса тела, 
- момент инерции тела относительно вертикальной оси, проходящей через центр масс тела. Из уравнения неголономной связи имеем
|
|
|
.
Составим выражение работы действующих усилий на возможных перемещениях
Найдем обобщенные силы
.
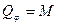Тогда уравнения (4.18) примут вид
Присоединяя к этим уравнениям уравнение связи 
, получим систему из четырех уравнений с четырьмя неизвестными.
Зная , из третьего уравнения можно найти 
. Ниже будем полагать эту функцию уже определенной.
Умножая обе части первого равенства на 
и вычитая его из второго уравнения, получим
.
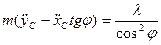Продифференцировав уравнение связи, получим 
.
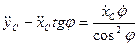Тогда выражение для множителя Лагранжа будет
.
Подставляя его в первое дифференциальное уравнение, получим линейное дифференциальное уравнение второго порядка для определения 
:
.
Полагая 
; 
, перепишем полученное уравнение в виде
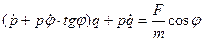
и подчиним 
условию 
, т.е. положим 
.
При этом будет
.
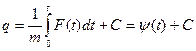Выберем начальные условия:
при 
: 
, 
, 
.
Тогда, окончательно, будем иметь:
Из полученных выражений следует, что величина скорости центра масс зависит от заданной силы и не зависит от момента , что является следствием перпендикулярности реакции неголономной связи 
и скорости центра масс 
.
Траектория центра масс зависит от обоих усилий.
В частном случае при движении по инерции (
) со скоростью 
уравнения траектории будут
, 
.
Это уравнения окружности, сдвинутой в положительном направлении оси 
на величину своего радиуса 
.
Вопросы и задачи для самоконтроля
1. В чем преимущества применения уравнений Лагранжа второго рода перед общим уравнением динамики?
2. Запишите уравнения Лагранжа второго рода для консервативных и неконсервативных механических систем.
3. Что такое кинетический потенциал и как записываются уравнения Лагранжа второго рода через эту характеристику?
4. Какие обобщенные координаты являются циклическими? Что такое циклический интеграл?
5. Достаточно ли составления уравнений Лагранжа второго рода и начальных условий для решения задачи о движении механической системы с неидеальными связями? Какие пути нахождения величин реакций неидеальных связей могут быть использованы?
6. В чем особенность задач о движении механической системы с неудерживающими связями? Чем обусловлено разделение движения на этапы? Что можно сказать о схеме сил, действующих на этапе? Как связать положение и скорость точки механической системы для предыдущего и последующего этапов движения?
|
|
|
