 |
Условия равновесия механической системы в обобщенных координатах и силах
|
|
|
|
Условие (2.1) можно записать в обобщенных координатах и силах. Для этого в (2.1) подставим (1.10), тогда
(2.3)
где 
- обобщенная сила.
Если возможные перемещения 
(
) выбраны независимыми (их число соответствует числу степеней свободы механической системы), то для выполнения равенства (2.3) необходимо, чтобы все коэффициенты при независимых возможных перемещениях по отдельности равнялись нулю:
. (2.4)
Для консервативной системы это условие соответствует экстремуму потенциальной энергии в положении равновесия системы:
; . (2.5)
Итак, в случае равновесия несвободной механической системы, подчиненной идеальным удерживающим связям, все обобщенные силы должны равняться нулю.
В том случае, когда наложенные на систему связи голономные, независимые возможные перемещения соответствуют независимым обобщенным координатам.
Если связи, наложенные на систему не идеальны, то их реакции (например, силы трения) надо отнести к задаваемым силам; эти силы должны быть рассчитаны предварительно каким-либо образом.
ПРИМЕР 2.1 (задача 46.24 из [5]). Составная балка АЕ, лежащая на двух опорах А и С, состоит из трех балок АВ, ВD и DE, шарнирно соединенных в точках B и D. Балка DE в сечении Е защемлена в стене. К балкам приложены четыре равные вертикальные силы Р. Размеры указаны на рисунке 2.1. Определить вертикальную составляющую реакции в сечении Е.
РЕШЕНИЕ. Изображенная несвободная механическая система из трех шарнирно соединенных балок не может двигаться, т.е. имеет ноль степеней свободы. Дадим точке Е возможность перемещаться по вертикали, при этом добавим к действующим силам неизвестную вертикальную силу 
. Новая механическая система обладает одной степенью свободы.
|
|
|
Дадим системе возможное перемещение 
по вертикали (например, вниз; конфигурация системы, допускаемая связями в этом случае, изображена на рис.2.2). Составим выражение для работы всех действующих сил на возможных перемещениях точек их приложения и потребуем, что бы эта работа была равна нулю (т.е. выполнялось условие (2.1)). Тогда
,
здесь 
- возможное перемещение точки приложения 
-ой силы (нумерация сил 
и возможных перемещений точек их приложения принята слева на право).
Поскольку связи, наложенные на систему, геометрические, можно все линейные возможные перемещения выразить через два возможных угловых перемещения; в свою очередь, связь между угловыми перемещениями может быть получена из выражения для линейного возможного перемещения точки В. Тогда 
; 
; 
; 
;
; при этом направления возможных перемещений учтены знаками слагаемых при составлении суммы работ.
Выразим все возможные перемещения через какое-то одно, выбранное за возможное перемещение по обобщенной координате (например ) и вынесем его за скобки.
.
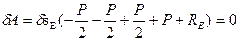Полученное произведение может быть равно нулю только в случае равенства нулю выражения в скобках (его смысл – обобщенная сила для возможного перемещения по обобщенной координате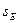 
).
Отсюда 
.
Замечание. При необходимости расчета других составляющих реакции в точке Е или реакций в точках А либо С, алгоритм действий не изменяется: снимается ограничение на перемещение, но прикладывается соответствующее неизвестное усилие (например возможность поворота относительно точки Е обуславливает приложение в точке Е неизвестного момента). Новой механической системе, обладающей одной степенью свободы, дается возможное перемещение. Составляется выражение для суммы работ всех действующих сил на возможных перемещениях точек их приложения. Принцип возможных перемещений позволяет приравнять составленную сумму к нулю. Записываются уравнения связей; с их помощью возможные перемещения в уравнении для суммы работ выражаются через какое-то одно с выносом его за скобки. Приравнивание нулю выражения в скобках (его физический смысл – обобщенная сила) дает уравнение для нахождения неизвестного усилия.
|
|
|
ПРИМЕР 2.2 (задача 46.10 из [5]). В кулисном механизме при качании рычага ОС вокруг горизонтальной оси О ползун А, перемещаясь вдоль рычага ОС, приводит в движение стержень АВ, движущийся в вертикальных направляющих К (см. рис.2.3).
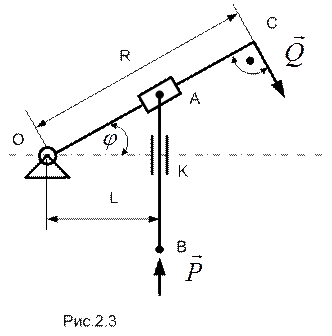
Даны размеры: 
. Какую силу 
надо приложить перпендикулярно кривошипу 
в точке 
, чтобы уравновесить силу 
, направленную вдоль стержня 
вверх?
РЕШЕНИЕ. Рассматриваемая механическая система обладает одной степенью свободы. Дадим системе возможное перемещение, соответствующее повороту рычага по часовой стрелке, и составим сумму работ всех действующих сил на возможных перемещениях точек их приложения. При равновесии эта сумма должна быть равна нулю:
.
Поскольку рассматриваемая механическая система обладает стационарными и голономными связями, возможные перемещения ее точек относятся как соответствующие скорости; тогда
, откуда 
.
Нахождению соотношений между скоростями точек механической системы было уделено достаточно внимания при изучении курса кинематики, поэтому действия, выполненные ниже, будут комментироваться кратко.
Скорость точки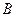 
равна абсолютной скорости точки 
, т.к. звено движется в вертикальных направляющих поступательно. Разложив скорость точки на относительную (вдоль рычага ) и переносную (перпендикулярную рычагу ) составляющие, получим для последней выражение
.
Угловую скорость вращения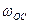 
рычага можно получить, разделив скорость переносного движения точки (т.е. скорость точки рычага, совпадающую с точкой в данный момент времени) на расстояние от нее до оси вращения (
). Скорость точки рычага есть произведение угловой скорости рычага 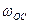на его длину, т.е.
.
Окончательно имеем 
.
Заметим, что алгоритм расчета остался прежним, хотя соотношения между возможными перемещениями точек системы были найдены из соотношений кинематики, а не геометрии, как это было в предыдущем примере.
|
|
|
ПРИМЕР 2.3. Механическая система (см. рис.2.4), состоящая из двух соосных (насаженных неподвижно на единую ось) блоков и двух грузов, прикрепленных к земле пружиной и демпфером, находится в положении статического равновесия. Зная жесткость пружины 
, веса грузов и радиусы блоков, определить удлинение пружины.
РЕШЕНИЕ. Рассматриваемая механическая система обладает одной степенью свободы. Заменим действие пружины силой упругости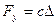 
, где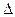 
- удлинение пружины в положении статического равновесия механической системы. Сила со стороны демпфера 
, пропорциональная скорости движения его поршня, при покое системы отсутствует.
Дадим системе возможное перемещение и запишем выражение для суммы работ всех действующих сил на возможных перемещениях точек их приложения; сумму приравняем к нулю и вынесем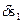 
за общую скобку. Тогда
.
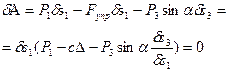При получении выражения учтено, что элементарная работа силы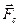 
равна нулю, так как сила приложена в мгновенном центре скоростей колеса 3.
Запишем уравнения связей, используя соотношения кинематики:
;
;
.
Для рассматриваемой механической системы возможные перемещения пропорциональны соответствующим скоростям, т.е.
; 
.
Приравняв нулю выражение в круглых скобках, получим выражение для расчета статического удлинения пружины: 
.
ПРИМЕР 2.4 (задача 46.21 из [5]). К концам нерастяжимой нити привязаны грузы А и В одинаковой массы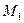 
.
От груза А нить проходит параллельно горизонтальной плоскости, огибает неподвижный блок С, охватывает подвижный блок Д, затем огибает неподвижный блок Е, где к другому концу нити привязан груз В. К оси подвижного блока Д подвешен груз К массы 
(см. рис.2.5). Определить массу 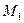каждого из грузов А и В и коэффициент трения скольжения 
груза А о горизонтальную плоскость, если система грузов находится в покое. Массами нити и блока Д пренебречь.
РЕШЕНИЕ. Рассматриваемая механическая система обладает двумя степенями свободы. Выберем в качестве независимых обобщенных координат горизонтальное перемещение 
груза А и вертикальный подъем 
груза В. Тогда, в силу нерастяжимости нити, опускание по вертикали 
центра блока Д (и груза К) будет зависеть от выбранных обобщенных координат.
|
|
|
Для получения уравнения связи рассмотрим рис.2.6, на котором
изображены скорости точек блока Д при его плоскопараллельном движении.
Анализ рисунка позволяет записать кинематическое уравнение голономной (интегрируемой) стационарной связи
.
В этом случае возможные перемещения относятся между собой как соответствующие скорости, т.е.
.
Обобщенные силы, как указывалось выше, могут быть найдены тремя путями (см. (1.9), (1.11) либо (1.22)). Ниже приведен подход, базирующийся на независимости выбранных обобщенных координат и опирающийся на формулу (1.11).
Дадим системе возможное перемещение, обусловленное изменением обобщенной координаты , оставив при этом другую обобщенную координату без изменения, т.е. 
.
При этом у системы остается как бы только одна степень свободы. Составим выражение для суммы работ всех сил на возможных перемещениях точек их приложения и приравняем ее к нулю:
.
При 
возможное перемещение 
. Силу трения рассчитаем предварительно как 
и отнесем к активным силам. С учетом этого выражение для работы на возможном перемещении 
будет
.
Выражение в круглых скобках есть обобщенная сила, соответствующая возможному перемещению по первой обобщенной координате; в положении равновесия системы она должна быть равна нулю. Таким образом, получаем первое уравнение для параметров системы:
.
Дадим системе возможное перемещение, обусловленное изменением обобщенной координаты ; при этом другую координату оставим без изменения, т.е. 
.
Составим сумму работ всех сил на возможных перемещениях точек системы и приравняем ее к нулю:
.
При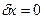 
возможное перемещение 
.
С учетом этого выражение для работы на втором возможном перемещении будет
.
Выражение в круглых скобках есть обобщенная сила, соответствующая возможному перемещению по второй обобщенной координате; в положении равновесия системы она так же должна быть равна нулю. Тогда второе уравнение для параметров системы будет:
.
Решив систему из двух уравнений, получим, что равновесие механической системы будет иметь место при 
; 
.
Вопросы и задачи для самоконтроля
1. Чем отличаются условия равновесия механической системы и условия ее покоя? Как формулируются условия равновесия механической системы с идеальными связями?
2. Что можно сказать о величине обобщенных сил в случае равновесия механической системы?
3. Какое число независимых уравнений равновесия можно составить для механической системы с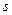 
степенями свободы?
4. Из механической системы, изображенной на рис.2.5, исключить пружину и демпфер. Определить, при каких значениях веса груза система будет сохранять состояние покоя, если для диска 3 задан коэффициент трения качения (см)? Какова особенность решения задачи о равновесии механической системы при наличии трения качения (либо сухого трения)?
|
|
|
|
|
|
