 |
Уравнение Лагранжа второго рода для консервативных систем
|
|
|
|
В случае действия на систему потенциальных сил, обобщенные силы могут быть найдены по формулам из параграфа 1.3 как
, 
(4.5)
где 
- потенциальная энергия системы.
Тогда уравнения Лагранжа принимают вид
, (4.6)
Если на систему действуют силы, имеющие потенциал и неконсервативные силы, то получим уравнения Лагранжа в виде
, (4.7)
Уравнения (4.6) можно преобразовать путем введения функции Лагранжа 
, называемой кинетическим потенциалом.
Выразим кинетическую энергию через кинетический потенциал и возьмем соответствующие производные из (4.6). Тогда, с учетом зависимости потенциальной энергии только от обобщенных координат, получим:
; 
; 
.
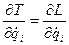Окончательно имеем 
, (4.8)
Уравнения (4.6) или (4.8) называются уравнениями Лагранжа для консервативных систем.
ПРИМЕР 4.3 Составить уравнения движения двойного математического маятника, изображенного на рис. 4.3.
РЕШЕНИЕ. Составим выражение для кинетической энергии двойного математического маятника:
.
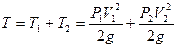Скорость второй тяжелой точки 
, где 
- скорость переносного движения с первой тяжелой точкой, а 
- относительного вращения вокруг первой точки. Тогда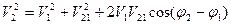 
.
Выбрав, как и ранее, в качестве независимых обобщенных координат углы с вертикалью 
и 
, выражение для кинетической энергии можно привести к виду:
.
Вычислим соответствующие производные:
; 
;
;
;
Для системы, изображенной на рис.4.2, ранее (см. пример 1.3) было составлено выражение для потенциальной энергии и найдены обобщенные силы, соответствующие обобщенным координатам и :
;
;
.
Подставив полученные выражения в (4.6), получим систему из двух дифференциальных уравнений второго порядка, описывающих движение двойного математического маятника:
|
|
|
Циклические координаты. Циклические
Интегралы
Обобщенные координаты, не входящие в явном виде в кинетический потенциал 
, называются циклическими координатами.
Предположим, что среди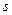 
обобщенных координат 
являются циклическими.
Тогда, в соответствии с определением циклических координат, производные от кинетического потенциала по этим координатам равны нулю:
; 
.
В этом случае уравнения (4.8) принимают вид
; .
Откуда 
; . (4.9)
Равенства (4.9) называются циклическими интегралами.
Как видно, циклические координаты позволяют сразу записывать первые интегралы, что значительно упрощает решение уравнений Лагранжа. По существу уравнения (4.9) представляют собой соотношения между кинематическими характеристиками движения, а учет каждого такого соотношения позволяет понизить на единицу порядок системы дифференциальных уравнений Лагранжа. В итоге вместо решения системы дифференциальных уравнений порядка 2 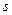при 
циклических координатах требуется решать систему дифференциальных уравнений порядка 
. Поэтому обобщенные координаты следует выбирать так, чтобы возможно большее их число было циклическими.
ПРИМЕР 4.4 (задача 48.28 из [5]). Призма А массы 
скользит по гладкой боковой грани призмы В массы 
, образующей угол 
с горизонтом (см. рис.4.4.а).
Определить ускорение призмы В. Трением между призмой В и горизонтальной плоскостью пренебречь.
РЕШЕНИЕ. Система обладает двумя степенями свободы, так как для остановки всех тел системы необходимо зафиксировать две координаты, например перемещение 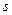призмы А относительно призмы В и горизонтальное перемещение 
самой призмы В.
Именно эти перемещения выберем в качестве независимых обобщенных координат. Составляя выражение для кинетической энергии учтем, что призма А участвует в двух движениях – переносном с призмой В и движении относительно нее (см. рис.4.4.б).
|
|
|
Тогда
.
Составим выражение для потенциальной энергии (ее значение в начальном положении принято за нулевое):
.
Подставим выражения энергий в функцию Лагранжа
.
Выполнив ряд формальных действий, довольно легко получить систему из двух дифференциальных уравнений Лагранжа, описывающих движение тел механической системы
;
.
Решив систему уравнений, найдем ускорение призмы В:
.
Заметим, что обобщенная координата является циклической, так как отсутствует в выражении кинетического потенциала. В таком случае мы могли без составления уравнений Лагранжа сразу записать выражение
,
совпадающее с первым интегралом первого дифференциального уравнения. Полученное соотношение показывает, что абсцисса центра масс механической системы, в зависимости от начальных условий, либо сохраняет свою величину, либо изменяется пропорционально времени.
|
|
|
