 |
Уравнение Лагранжа второго рода
|
|
|
|
Вывод уравнений
Рассмотрим механическую систему из n материальных точек 
(
), ограниченную 
идеальными голономными связями. Ее положение в пространстве определим независимыми обобщенными координатами 
(
), число которых соответствует числу степеней свободы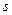 
механической системы. Обратимся к общему уравнению динамики (3.4) и запишем его в обобщенных координатах. Работа активных сил на возможных перемещениях, согласно (1.8) и (1.10), будет
. (4.1)
Преобразуем оставшиеся слагаемые
. (4.2)
Выражение в скобках представим так
, (4.3)
где 
- кинетическая энергия системы, 
- 
ая обобщенная скорость.
Таким образом, общее уравнение динамики с учетом (4.3), (4.1) и (1.2) можно представить в виде
.
Поскольку 
независимы, равенство выполняется, когда
; . (4.4)
Мы получили систему обыкновенных дифференциальных уравнений второго порядка относительно 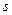неизвестных функций 
, определяющих закон движения механической системы. Число уравнений равно числу степеней свободы; форма их записи не зависит от конкретного выбора обобщенных координат; они не содержат реакций идеальных голономных связей. Уравнения (4.4) называются уравнениями Лагранжа второго рода.
ПРИМЕР 4.1. Используя Уравнения Лагранжа второго рода, составить дифференциальное уравнение движения первого груза механической системы из примера 3.1.
РЕШЕНИЕ. На рис.2.4 изображена механическая система с действующими на нее внешними силами.
Выберем за обобщенную координату линейное перемещение первого груза. Уравнения кинематических связей останутся прежними:
или 
;
или 
;
или 
.
Составим выражение для кинетической энергии механической системы:
.
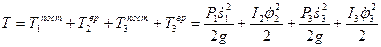При записи учтено, что мгновенный центр скоростей диска, катящегося без скольжения, расположен в точке его соприкосновения с плоскостью.
|
|
|
Вынесем за скобки квадрат обобщенной скорости
.
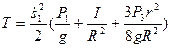При получении результата учтено, что осевой момент инерции однородного диска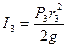 
.
Частная производная от кинетической энергии по обобщенной координате будет равна нулю, так как полученное выражение от обобщенной координаты не зависит.
Частная производная от кинетической энергии по обобщенной скорости будет
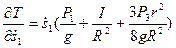. Производная по времени от частной производной кинетической энергии по обобщенной скорости будет
.
Для вычисления обобщенной силы дадим системе возможное перемещение. Составим сумму работ всех внешних сил на соответствующих возможных перемещениях и вынесем возможное перемещение по обобщенной координате 
за скобки:
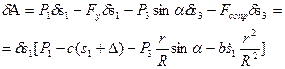
Выражение в квадратных скобках и есть обобщенная сила для возможного перемещения по выбранной обобщенной координате.
После подстановки в (4.4) выражений для частных производных и обобщенной силы, а так же учета условия равновесия (см. пример 2.3), окончательно имеем 
Полученное уравнение совпадает с результатом решения примера 3.1.
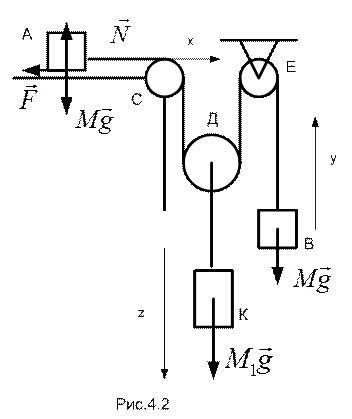
ПРИМЕР 4.2. (задача 48.26 из [5]). К концам нерастяжимой нити привязаны грузы А и В одинаковой массы 
. От груза А нить проходит параллельно горизонтальной плоскости, огибает неподвижный блок С, охватывает подвижный блок Д, затем огибает неподвижный блок Е, где к другому концу нити привязан груз В. К оси подвижного блока Д подвешен груз К массы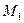 
(см. рис.4.2). Коэффициент трения скольжения 
груза А о горизонтальную плоскость известен. При каком условии груз К будет опускаться вниз, если начальные скорости всех грузов равнялись нулю? Найти ускорение груза К. Массами нити и блоков пренебречь.
РЕШЕНИЕ. Рассматриваемая механическая система отличается от системы, рассмотренной в примере 2.4, индексами масс грузов. Она обладает двумя степенями свободы. Выберем, как и при решении примера 2.4, в качестве независимых обобщенных координат горизонтальное перемещение 
груза А и вертикальный подъем 
груза В. Тогда, в силу нерастяжимости нити, опускание по вертикали 
центра блока Д (и груза К) будет зависеть от выбранных обобщенных координат.
|
|
|
Уравнение кинематической связи были получены при решении примера 2.4
.
Составим выражение для кинетической энергии системы
и возьмем соответствующие производные:
; 
;
; 
;
;
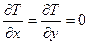Выражения для обобщенных сил были получены при решении примера 2.4. Изменив индексы масс, (так как в задачах 46.21 и 48.26 из [5] они не совпадают) имеем:
;
.
Теперь составим систему из двух дифференциальных уравнений второго порядка
;
.
Сложим полученные уравнения и учтем результат дифференцирования уравнения кинематических связей 
. Окончательно получим
.
Очевидно, что груз К будет двигаться вниз, если числитель полученного выражения положителен, т.е. при 
.
|
|
|
