 |
Работа силы на элементарном и возможном перемещении
|
|
|
|
Напомним понятие элементарной работы, введенное нами при выводе теоремы об изменении кинетической энергии в [8] как скалярное произведение силы на элементарное перемещение точки ее приложения
.
Заметим, что в общем случае введенная величина не является полным дифференциалом выражения работы (работа силы может зависеть не только от координат точки ее приложения; на это обстоятельство указывает знак апострофа).
При естественном задании движения материальной точки 
и 
где 
- проекция силы на касательную к траектории, 
- мощность силы, а 
- скорость точки.
В случае задания силы и радиуса - вектора точки в декартовой координатной системе, выражение для элементарной работы принимает вид: 
Если скорость движения точки рассматривается как сумма скоростей в относительном и переносном движениях (справедлива формула из [6]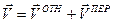 
), выражение для элементарной работы будет
.
Элементарной работой системы сил, приложенных к точкам механической системы, называют сумму элементарных работ вида
, где 
- число материальных точек, формирующих механическую систему.
Если силы, действующие на точки механической системы, разделить на внешние и внутренние, то их элементарная работа может быть представлена в виде суммы:
.
Напомним, что в системе с геометрически неизменяемыми связями 
.
По аналогии с элементарной работой может быть введено понятие работы силы на возможном перемещении (в некоторых источниках - виртуальной работы) как 
.
Очевидно, что для систем со стационарными голономными связями все формулы для вычисления элементарной работы будут справедливы при замене знака 
на 
(так как в этом случае элементарное перемещение является одним из возможных).
|
|
|
Заметим, что в литературе по аналитической механике под идеальными связями принято понимать связи, работа реакций которых на возможных перемещениях равна нулю. Для систем со стационарными голономными связями это определение эквивалентно приведенному во введении.
Обобщенные силы
Наряду с введенными ранее понятиями обобщенных координат, обобщенных скоростей и ускорений [6, 8], введем понятие обобщенных сил.
Рассмотрим систему из материальных точек, на которую действуют внешние силы 
; 
. Вычислим работу внешних сил на возможных перемещениях 
() как
. (1.6)
Определим из (1.2) возможное перемещение , введя независимые обобщенные координаты 
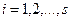. Поскольку связи, наложенные на систему, голономны,
имеем 
; 
. (1.7)
Подставив (1.7) в (1.6), получим
.
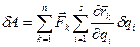Изменив порядок суммирования по индексам 
и 
, будем иметь
. (1.8)
Величины
(1.9)
называют обобщенными силами, соответствующими возможным перемещениям 
;
при выводе учтено разложение векторов 
и 
на оси неподвижной декартовой координатной системы.
Подставляя (1.9) в (1.8), получим
. (1.10)
В случае, когда возможные перемещения независимы, можно сообщить системе только одно возможное перемещение 
, полагая остальные равными нулю, т.е.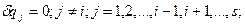 
. Далее следует вычислить 
всех действующих сил на возможных перемещениях точек их приложения 
. Выразив последние через (используя уравнения связей), вынесем его за скобки. Выражение в скобках и будет обобщенной силой, соответствующей возможному перемещению механической системы, т.е.:
. (1.11)
Последовательно вычисляя работу на каждом из независимых возможных перемещений , можно определить соответствующие им обобщенные силы 
.
Заметим, во-первых, что размерность обобщенной силы, определяемой из (1.11), может быть любой. Например, при выборе в качестве обобщенной координаты угла поворота, обобщенная сила имеет размерность момента силы. Во-вторых, согласно (1.9), обобщенную силу формируют силы, приложенные в различных точках механической системы. Оба отмеченных обстоятельства подчеркивают удачность предложенного названия.
|
|
|
ПРИМЕР 1.2. Выбрать обобщенные координаты и определить обобщенные силы для двойного математического маятника, изображенного на рис.1.2.
РЕШЕНИЕ. Положение двойного маятника можно определить двумя углами 
и 
, которые и примем за обобщенные координаты (система имеет две степени свободы). Отсчет углов происходит от вертикальных линий (поскольку направление вертикалей не изменяется, выбранные координаты называются абсолютными).
Сначала воспользуемся подходом, использующим формулу (1.9).
Составим выражения для действующих сил и радиусов - векторов точек их приложения, выразив последние через выбранные обобщенные координаты:
; 
; 
.
Для нашего случая формула (1.9) будет иметь вид
; 
Взяв соответствующие производные и выполнив действия формального характера, получим
; 
.
Теперь воспользуемся подходом, использующим формулу (1.11).
Для определения обобщенной силы 
, соответствующей первой обобщенной координате , дадим механической системе возможное перемещение 
, оставляя вторую обобщенную координату без изменения, т.е. 
. Составим сумму работ сил 
и 
на заданном возможном перемещении: 
. Вертикальные смещения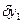 
и 
точек приложения сил, вызванные изменением угла (при сохранении неизменным угла ), найдутся из соотношений 
. Подставляя эти значения в выражение для работы на возможном перемещении, получим
.
Откуда .
Для нахождения обобщенной силы 
, соответствующей обобщенной координате , придадим углу приращение 
, но угол оставим без изменения, т.е. 
.
Для работы силы 
на заданном возможном перемещении получим выражение
.
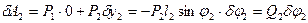Тогда обобщенная сила будет
.
Естественно, что найденные разными приемами обобщенные силы одинаковы.
На взгляд авторов действия при использовании формулы (1.9) хотя и носят несколько формальный характер, более удобны при исследовании поведения механических систем с большим числом степеней свободы.
|
|
|
