 |
Силовое поле. Потенциальная энергия. Обобщенные силы для консервативных систем
|
|
|
|
Будем называть силовым полем область пространства, в каждой геометрической точке которого на помещенную в него материальную точку действует сила, однозначно определенная по величине и направлению в любой момент времени [2].
Таким образом, в силовом поле должны быть известны три функции – проекции силы на оси координат. Например, для декартовой системы это
.
Силовое поле называется нестационарным, если проекции силы в явном виде зависят от времени; если проекции силы от времени не зависят, то поле стационарное и
. (1.12)
Ниже ограничимся рассмотрением только стационарных силовых полей. Среди них важное место занимают поля, у которых работа сил, приложенных к материальной точке, не зависит от вида траектории и закона движения по ней; величина работы определяется только начальным и конечным положениями точки в пространстве.
Силовое поле называется консервативным, если существует такая функция координат 
, называемая потенциальной энергией, что проекции силы могут быть представлены через нее следующим образом:
. (1.13)
Покажем, что для консервативных сил работа зависит только от начального и конечного положений точки и не зависит от вида траектории и закона движения по ней.
Заметим, что элементарная работа консервативных сил равна полному дифференциалу потенциальной энергии, взятому с обратным знаком:
(1.14)
Тогда, пользуясь формулой для вычисления работы из [2], получим
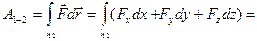
. (1.15)
Под знаком интеграла по кривой 
от точки 1 до точки 2 стоит полный дифференциал от функции , поэтому выражение для работы принимает вид
. (1.16)
Как видно из формул (1.13), (1.14) и (1.16), потенциальная энергия определяется с точностью до постоянного слагаемого. Этим обстоятельством можно воспользоваться, назначив в некоторой точке нулевое значение потенциальной энергии. Выбрав, например, в качестве такой точки начало координат, получим
|
|
|
. (1.17)
В этом случае потенциальная энергия в данной точке равна работе, производимой силами поля при перемещении точки из заданного положения в начало координат.
В некоторых источниках независимость работы от вида траектории принимают за определение консервативности силового поля. С доказательством тождественности обоих утверждений можно ознакомиться, например, в [2].
Независимость работы от вида траектории определяет еще одно свойство консервативности поля: - работа по любому замкнутому контуру в консервативном силовом поле равна нулю (см.(1.16)).
По определению, силовое поле консервативно, если справедливы формулы (1.13). Отсюда вытекают простые критерии консервативности силового поля. Дифференцируя (1.13), получим
и т.д.
Используя свойство независимости смешанных производных от порядка дифференцирования, окончательно имеем
. (1.18)
Условия (1.18) вытекают из консервативности силового поля и являются необходимыми.
Покажем, как вычисляется потенциальная энергия для некоторых часто встречающихся силовых полей.
Потенциальная энергия поля силы тяжести. Совмещая плоскость 
с горизонтальной плоскостью, для проекций силы тяжести будем иметь 
.
Нетрудно проверить, что условия (1.18) выполняются. Используя (1.17), получим
. (1.19)
Потенциальная энергия поля центральных сил. Центральной будем называть силу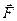 
, которая в любой точке пространства направлена по прямой, соединяющей рассматриваемую точку с точкой, называемой центром; при этом модуль силы зависит только от расстояния 
между точкой и центром.
Если центр выбрать в начале координат, то 
, где 
- радиус-вектор точки.
Учитывая, что 
, а проекции силы на оси декартовой координатной системы есть
|
|
|
,
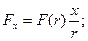
можно, выполнив проверку условий консервативности (1.18) для центральной силы, убедиться в их выполнимости.
Теперь получим выражение для потенциальной энергии, полагая, что точка переходит из произвольного положения 
в некоторое фиксированное 
. Тогда
(1.20)
В частности, когда центральной силой является гравитационная сила, выражение для потенциальной энергии примет вид
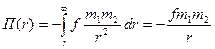, где 
- постоянная тяготения, 
- массы притягивающихся материальных точек, - расстояние между ними. При выводе за была принята бесконечно удаленная точка.
Потенциальная энергия восстанавливающей силы пружины. Примем за фиксированную точку , в которой равна нулю потенциальная энергия, положение конца недеформированной пружины. Пусть длина пружины в недеформированном состоянии равна 
, а в положении равна . Тогда 
. Знак «-» означает, что направление радиуса - вектора точки и восстанавливающей силы пружины (силы упругости) противоположны. Подставив выражение силы в (1.20), получим
,
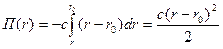или 
, где 
- модуль приращения длины пружины.
Из полученных формул следует, что работа восстанавливающей силы пружины при перемещении ее конца из положения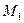 
в положение 
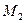равна
. (1.21)
Для вычисления обобщенных сил в консервативных системах следует проекции сил (1.13) внести в уравнения (1.9). Тогда
. (1.22)
При выводе учтено, что первоначально выражение для потенциальной энергии было записано через декартовы координаты точек механической системы, которые позже были записаны через выбранные обобщенные координаты.
ПРИМЕР 1.3. Для системы, изображенной на рис.1.2, составим выражение для потенциальной энергии и найдем обобщенные силы, соответствующие обобщенным координатам 
и 
.
Для этого вычислим работу сил 
и 
при перемещении системы из отклоненного положения в горизонтальное (принятое за положение с нулевой потенциальной энергией):
.
Выполнив дифференцирование (1.22), получим
;
.
Естественно, что выражения для обобщенных сил совпадают с выражениями, полученными ранее.
Вопросы и задачи для самоконтроля
1. Дайте определение удерживающих, стационарных и голономных связей. Какие из них описываются уравнениями, а какие – неравенствами? Уравнения каких связей содержат время в явном виде? Как называются связи, из уравнений которых не удается исключить производные по обобщенным координатам?
|
|
|
Какие связи называют идеальными?
2. Механическая система состоит из трубки и двух масс, находящихся внутри нее, как это показано на рисунке. Массы соединены с трубкой и между собой пружинами. Трубка вращается в плоскости страницы с заданной угловой скоростью 
. Определите число степеней свободы механической системы. Какие связи наложены на ее элементы?
3. Дайте определение возможного перемещения элемента механической системы. Сравните элементарное и возможные перемещения точки механической системы для случаев наложения стационарной и нестационарной связей.
4. Какие координаты следует принимать в качестве обобщенных? Как вычислять соответствующие им обобщенные силы и почему они так называются? В качестве примера для механической системы, изображенной на рис. 2.4 вычислите обобщенные силы, соответствующие возможным перемещениям груза 1 и колеса 2.
5. Какое силовое поле называется консервативным? По какому критерию можно убедиться в его консервативности?
Что необходимо знать о траектории и законе движения по ней при вычислении работы сил поля в этом случае?
6. Как составить выражение для потенциальной энергии?
7. Как вычислить обобщенные силы, если известно выражение для потенциальной энергии механической системы?
|
|
|
