 |
Элементарные и возможные перемещения
|
|
|
|
Рассмотрим систему из 
материальных точек с координатами 
, на которую действуют силы 
, и движение которой ограничено геометрическими связями:
.
Перемещение любой точки 
зависит от вида и характера связей, действующих сил и начального состояния. Будем различать два вида бесконечно малых перемещений – элементарное действительное и возможное (виртуальное).
Элементарными действительными называют те бесконечно малые перемещения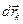 
точек системы, которые согласуются со связями и реально возникают в системе под влиянием внешних сил и начальных условий. Например в декартовой координатной системе, где радиус-вектор 
-ой точки 
, а 
- ее координаты, эти перемещения могут быть записаны в следующей форме:
(1.1)
Напомним, что в курсе кинематики для элементарного перемещения использовалось выражение 
, имеющее достаточно ясный физический смысл (здесь 
- скорость -ой точки).
Возможными (или виртуальными) перемещениями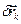 
называют любые (иногда и действительные) бесконечно малые перемещения точек системы, допускаемые связями в рассматриваемый момент времени 
.
В отличие от действительных, возможные перемещения рассматриваются вне зависимости от действующих сил и начальных условий. Эти перемещения можно понимать как некоторый геометрический образ, отражающий не действительное движение системы, а в принципе возможный ее переход в смежную конфигурацию, зависящую от наложенных на систему связей; при этом изменение связей во времени отсутствует.
В таком случае возможные перемещения представляют собой приращения радиусов-векторов 
точек, не зависящие от времени , т.е. неполный «дифференциал»:
(1.2)
Сравнивая (1.1) и (1.2), можно сделать вывод, что элементарные действительные перемещения системы 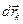() совпадают с одним из ее возможных перемещений 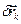() в том случае, если на механическую систему наложены геометрические стационарные связи.
|
|
|
Заметим, что в этом случае возможные перемещения относятся между собой как соответствующие элементарные перемещения; в свою очередь элементарные перемещения относятся друг к другу как соответствующие скорости (т.к. скорость есть частное от деления элементарного перемещения на 
). Таким образом, в системах с геометрическими (голономными) стационарными связями возможные перемещения относятся между собой, как соответствующие скорости; умению находить соотношения между скоростями точек механической системы был посвящен курс кинематики.
Посмотрим теперь, какие ограничения накладывают связи на возможные перемещения механической системы. Пусть система состоит из материальных точек . При условии, что все точки системы свободны, мы имеем 3 произвольных перемещения. В случае выбора декартовой координатной системы им будут соответствовать возможные перемещения 
().
Если система подчинена 
стационарным голономным связям
, 
(1.3)
то, найдя дифференциалы от уравнений связей, получим ограничений, которым должны удовлетворять элементарные перемещения точек механической системы:
Как указывалось выше, у таких механических систем элементарные перемещения входят в число возможных; в этом случае выражения для возможных перемещений будут иметь аналогичную структуру:
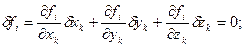
(1.4)
Отсюда следует, что произвольными остаются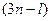 
перемещений. Это число совпадает с числом степеней свободы 
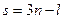рассматриваемой механической системы. Заметим, что в главе 3 [6] на стр.7 число степеней свободы определено «по координатам». Для голономных систем оба эти определения эквивалентны.
Если система подчинена голономным нестационарным связям
, 
(1.5)
|
|
|
то, полагая 
, получим такие же ограничения (1.4), как и в случае стационарных связей. Иначе будет с действительными перемещениями. В выражениях ограничений, налагаемых связями, войдут дополнительные слагаемые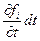 
(см. формулу(1.1)). Поэтому для случая нестационарных связей действительные перемещения точек системы,не находятся в числе возможных перемещений.
ПРИМЕР 1.1. Рассмотрим математический маятник постоянной длины , движущийся в плоскости 
(рис.1.1.а).
Точка 
под влиянием стационарной голономной связи 
движется по дуге окружности радиусом . Маятник постоянной длины в плоскости имеет одну степень свободы.
Из некоторого положения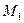 
, которое занимает точка в фиксированный момент времени, мысленно дадим малые приращения 
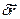. Они направлены по касательной к окружности, их бесчисленное множество (можно менять модуль и направление вдоль касательной) и все они являются возможными (или виртуальными) перемещениями. Если под действием внешней силы и (или) начальных условий маятник отклониться, например вправо, то действительное перемещение 
будет направлено по касательной к траектории и будет совпадать с одним из виртуальных перемещений (см.рис.1.1.а).
Пусть нить математического маятника удлиняется по известному закону 
.
В этом случае имеет место нестационарная голономная связь 
.
Фиксируя время 
, построим в данном положении 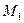траекторию маятника – окружность радиуса 
(рис.1.1.б).
Возможные перемещения 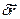направлены по касательной к этой окружности. Однако, в отличие от предыдущего случая, в рассматриваемом положении за время изменяется не только угол 
, но и длина . Учитывая это обстоятельство, получим, что действительное элементарное перемещение маятника не будет совпадать ни с одним из возможных перемещений 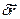(см. рис.1.1.б).
Введение понятия числа степеней свободы механической системы позволяет лучше понять физический смысл аксиомы об освобождении от связей: при освобождении системы от связей у нее появляются дополнительные степени свободы; для того, что бы движение освобожденной от связей системы совпадало с движением системы при наличии связей, вводятся дополнительные усилия – реакции связей. Таким образом, принцип освобождения от связей приводит к новой системе (свободной, но с дополнительными реакциями связей), которая должна двигаться так же, как и исходная (несвободная) система. Обе системы должны быть динамически эквивалентны (движение их точек одинаково), но кинематическая эквивалентность систем отсутствует, так как освобожденная система обладает большим числом степеней свободы.
|
|
|
Заметим, что для механической системы число независимых возможных перемещений равно числу степеней свободы.
Если связи, наложенные на систему, геометрические, то число независимых возможных перемещений будет совпадать с числом независимых обобщенных координат.
Если на систему наложены неголономные связи, то число независимых возможных перемещений (равное числу степеней свободы) оказывается меньше числа независимых обобщенных координат на количество уравнений неголономных связей.
|
|
|
