 |
Колебания линейной механической системы с двумя степенями свободы около положения устойчивого равновесия
|
|
|
|
5.5.1. Свободные колебания. Рассмотрим линейную изначально либо линеаризованную (см. пункт 5.4.1) произвольную консервативную систему с голономными и стационарными связями, имеющую две степени свободы. Положение системы будем определять обобщенными координатами 
и 
, отсчитываемыми от положения устойчивого равновесия.
Для такой системы кинетическая энергия имеет вид (5.1), потенциальная – (5.2). Воспользовавшись, например, уравнениями Лагранжа второго рода, можно получить систему дифференциальных уравнений вида
Принимая во внимание, что 
перепишем уравнения в виде
(5.24)
Будем искать их решение в форме
(5.25)
где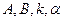 
- неизвестные постоянные.
Продифференцируем искомые выражения для обобщенных координат по времени дважды, подставим их в (5.24). Для удовлетворения этих равенств при любых 
, должны быть равны нулю коэффициенты при 
, т.е.
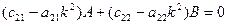. (5.26)
Система линейных уравнений относительно 
и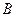 
имеет решение, отличное от нуля, в случае равенства нулю ее определителя
Раскрывая определитель, получим уравнение относительно 
(5.27)
Уравнение (5.27) называется уравнением частот или вековым уравнением. Оба корня этого уравнения вещественны и положительны. Извлечем из них корни и воспользуемся только положительными значениями 
и 
, которые называются частотами главных колебаний. Теперь вид (5.25) будет
.
Между числами 
есть связь. Установим ее, используя любое из уравнений (5.26), например, первое. Тогда
; 
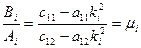. (5.28)
Каждому значению частоты и отвечают соответствующие значения 
и 
. Вычислив их, найдем
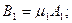
. (5.29)
Коэффициенты и имеют простой физический смысл – они показывают, во сколько раз амплитуда соответствующего главного колебания в одной из обобщенных координат больше (или меньше) амплитуды другой.
|
|
|
Теперь решение (5.25) примет вид
. (5.30)
В этом решении частоты , и коэффициенты , - известные числа (они рассчитываются по инерционно – жесткостным характеристикам механической системы), а 
- постоянные интегрирования, которые следует определить из задаваемых начальных условий.
В заключении отметим, что методы получения и интегрирования дифференциальных уравнений для линейных механических систем с двумя степенями свободы около положения устойчивого равновесия без всяких изменений могут быть распространены на линейные механические системы с большим числом степеней свободы.
ПРИМЕР 5.6. Для двойного математического маятника из примера 4.3 получить линейную модель и найти частоты ее главных колебаний.
РЕШЕНИЕ.
Для получения линейной модели воспользуемся выражениями для кинетической и потенциальной энергий, полученными при решении примера 4.3:
;
Для анализа малых колебаний заменим синусы и косинусы в выражениях энергий на члены не выше второго порядка малости в их разложений в степенной ряд Маклорена, т.е.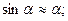 
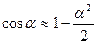. Тогда, после отбрасывания слагаемых высшего порядка малости по сравнению с остальными, получим:
;
.
Для получения математической модели малых колебаний воспользуемся уравнениями Лагранжа второго рода.
Вычислим соответствующие производные:
.
Составим уравнения Лагранжа для линеаризованной системы:
.
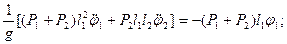
Приведем полученную систему линейных дифференциальных уравнений к виду (5.24):
.
Тогда уравнение частот (5.27) будет
.
Для окончательного решения целесообразно задать числовые значения соответствующих величин либо достаточно простые соотношения между ними.
Так, для частного случая 
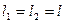, уравнение примет вид
.
Из него достаточно просто найти частоты главных колебаний
.
|
|
|
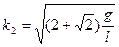