 |
Вынужденные колебания. Динамический гаситель колебаний.
|
|
|
|
Предположим, что к точкам линейной механической системы из пункта 5.5.1 приложены гармонически изменяющиеся во времени с частотой 
вынуждающие силы. Очевидно, что в таком случае дифференциальные уравнения движения будут иметь вид
;
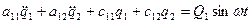(5.31)
а общее решение представлять сумму из решения (5.30) системы однородных уравнений (5.24) и частного решения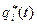 
, 
.
Будем искать частное решение в виде
, (5.32)
где 
- неопределенные коэффициенты, подлежащие определению; при этом предполагается, что резонанс в системе отсутствует, т.е. частота вынуждающего воздействия не совпадает ни с одной из частот главных колебаний (
; ). Продифференцируем искомые выражения для частного решения по времени дважды, подставим их в (5.31). Для удовлетворения этих равенств при любых 
, должны быть равны коэффициенты при 
в правой и левой частях уравнений системы, т.е.
. (5.33)
Система линейных уравнений относительно 
и 
имеет решение
(5.34)
где 
.
В качестве примера рассмотрим работу динамического гасителя колебаний. На рис.5.11.а схематично изображен механизм массой 
, установленный на упругих опорах суммарной жесткостью в вертикальном направлении 
.
Если частота возмущающей силы 
, создаваемой движущимися внутри механизма неуравновешенными частями, совпадает с частотой 
свободных колебаний механизма на опорах, будет иметь место резонанс. Что бы этого избежать, установим на механизме массу 
на пружине жесткостью 
. Новая механическая система, обладающая двумя степенями свободы, изображена на рис.5.11.б.
Выберем в качестве обобщенных координат 
и 
- абсолютные смещения по вертикали соответствующих масс от их положений статического равновесия. Мысленно отделим массы и , приложим к ним действующие силы; запишем для каждой из масс дифференциальное уравнение вертикального движения:
|
|
|
где 
- удлинение 
- ой пружины в положении статического равновесия.
Приведем уравнения системы к виду (5.31)
.
Будем искать частное решение в виде
.
Выполнив ряд действий, обсужденных выше, получим систему линейных уравнений (5.33) относительно и
.
Решение системы будет иметь вид:
.
Для того, что бы амплитуда вынужденных колебаний механизма была бы равна нулю, следует так подобрать массу и жесткость присоединяемого элемента, чтобы 
.
В таком случае присоединяемый элемент оказывается для механизма динамическим гасителем колебаний.
Вопросы и задачи для самоконтроля
1. Можно ли утверждать, что малые колебания любых механических систем описываются линейными дифференциальными уравнениями?
2. Как найти положение равновесия механической системы?
3. Как записать условие равновесия для консервативной механической системы?
4. Какое положения равновесия называется устойчивым?
Запишите критерии Сильвестра для механической системы с двумя степенями свободы.
5. Сформулируйте теорему Лагранжа – Дирихле. В каком случае невыполнение теоремы Лагранжа – Дирихле свидетельствует о неустойчивости положения равновесия (теорема Ляпунова)?
6. Почему частоту свободных колебаний иногда называют собственной частотой механической системы?
7. Какую последовательность образуют амплитуды колебаний механической системы с одной степенью свободы при наличии линейно – вязкого сопротивления?
8. Какая величина в предыдущем случае больше, период свободных колебаний механической системы без линейно – вязкого сопротивления или с ним?
9. Что называется вибрацией механической системы и как найти ее амплитуду?
10. Как выглядит амплитудно – частотная характеристика механической системы при действии гармонически изменяющаяся во времени вынуждающей силы.
|
|
|
11. Как выглядит амплитудно – частотная характеристика механической системы при действии гармонически изменяющегося во времени кинематического возбуждения.
12. Как влияет линейно – вязкое сопротивление на амплитудно – частотную характеристику механической системы?
13. Как, в общем случае, выглядит частотное уравнение для механической системы с одной степенью свободы? С двумя степенями свободы?
14. Что характеризуют коэффициенты форм главных колебаний 
?
15. Как подобрать параметры динамического гасителя колебаний?
Литература
1.Бутенин Н.В. Введение в аналитическую механику. Наука, Москва, 1971
2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Том 2., Наука, Москва, 1971
3. Гантмахер Ф.Р. Лекции по аналитической механике. изматгиз, Москва, 1960.
4. Яблонский А.А. Курс теоретической механики, Часть 2, Высшая школа, Москва, 1977 г.
5. Мещерский И.В. Задачи по теоретической механике. Лань, Москва, 2002 г.
6. Мелконян А.Л., Митрофанов В.П., Пановко Я.Г., Рощанский В.И., Черныш А.А. Теоретическая механика. Часть 1. Кинематика. Учебное пособие, Издательство ЛКИ, Ленинград, 1989 г.
7. Мелконян А.Л., Митрофанов В.П., Пановко Я.Г., Рощанский В.И., Черныш А.А. Теоретическая механика. Часть 2. Статика. Учебное пособие, Издательство ЛКИ, Ленинград, 1990 г.
8. Мелконян А.Л., Рощанский В.И., Черныш А.А. Теоретическая механика. Часть 3. Динамика. Учебное пособие, Издательство СПбГМТУ, Санкт-Петербург, 1996 г.
9. Чувиковский В.С. Численные методы расчетов в строительной механике корабля., Л., Судостроение, 1976 г.
|
|
|
